College Algebra
Answer/Discussion to Practice Problems
Tutorial 19: Radical Equations and Equations Involving Rational Exponents
WTAMU > Virtual Math Lab > College Algebra > Tutorial 19: Radical Equations and Equations Involving Rational Exponents
 Answer/Discussion
to 1a Answer/Discussion
to 1a
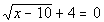
|
|
*Inverse of add. 4 is sub. 4
*Square root is by itself on one side of eq. |
If you square a square root, it will disappear. This is what
we want to do here so that we can get x out
from under the square root and continue to solve for it. |
|
*Inverse of taking the sq. root is squaring
it |
Step 3: If you
still have a radical left, repeat steps 1 and 2. |
No more radicals exist, so we do not have to repeat steps 1 and 2. |
Step 4: Solve
the remaining equation. |
|
*Inverse of sub. 10 is add. 10
|
|
|
Let's check to see if x = 26 is an extraneous
solution: |
|
*Plugging in 26 for x
*False statement |
Since we got a false statement, x =
26 is an extraneous solution.
There is no solution to this radical equation. |
 Answer/Discussion
to 1b Answer/Discussion
to 1b
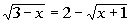
|
The radical in this equation is already isolated. |
If you square a square root, it will disappear. This is what
we want to do here so that we can get y out
from under the square root and continue to solve for it. |
|
*Inverse of taking the sq. root is squaring
it
*Right side is a binomial
squared |
Be careful on this one. It
is VERY TEMPTING to square the right side term by term and get 4
+ ( x + 1). However, you need to square
it as a side as shown above. Recall that when you square a binomial
you get the first term squared minus twice the product of the two terms
plus the second term squared. If you need a review on squaring a
binomial, feel free to go to Tutorial
6: Polynomials. |
Step 3: If you
still have a radical left, repeat steps 1 and 2. |
|
*Inverse of add. x and 5 is sub. x and 5
*Square root is by itself on one side of eq.
*Inverse of taking the sq. root is squaring
it
*Left side is a binomial
squared
|
Be careful on this one. It
is VERY TEMPTING to square the left side term by term and get 4 x squared
plus 4. However, you need to square it as a side as shown above.
Recall that when you square a binomial you get the first term squared plus
twice the product of the two terms plus the second term squared.
If you need a review on squaring a binomial, feel free to go to Tutorial
6: Polynomials. |
Step 4: Solve
the remaining equation. |
In this example, the equation that resulted from squaring both sides
turned out to be a quadratic equation.
If you need a review on solving quadratic equations feel free to go
to Tutorial 17: Quadratic Equations. |
Let's check to see if x = 3 is
an extraneous solution: |
|
*Plugging in 3 for x
*True statement |
Since we got a true statement, x = 3
is a solution. |
Let's check to see if x = -1 is an extraneous
solution: |
|
*Plugging in -1 for x
*True statement |
Since we got a true statement, x = -1
is a solution.
There are two solutions to this radical equation: x = 3 and x = -1. |
 Answer/Discussion
to 2a Answer/Discussion
to 2a
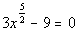
|
|
*Inverse of sub. 9 is add. 9
*Inverse of mult. by 3 is div. by 3
*rat. exp. expression is by itself on one side
of eq. |
If you raise an expression that has a rational exponent to the reciprocal
of that rational exponent, the exponent will disappear. This
is what we want to do here so that we can get x out from under the rational exponent and continue to solve for it. |
|
*Inverse of taking it to the 5/2 power
is taking it to the 2/5 power
|
Step 3: Solve
the remaining equation. |
In this example, the equation that resulted from raising both sides
to the 2/5 power turned out to be a linear equation.
Also note that it is already solved for x.
So, we do not have to do anything on this step for this example. |
Let's check to see if 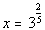 is an extraneous solution: is an extraneous solution: |
|
*Plugging in 3 to the 2/5 power for x
*True statement |
Since we got a true statement, 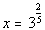 is
a solution. is
a solution.
There is one solution to this rational exponent equation: 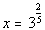 . . |
 Answer/Discussion
to 2b Answer/Discussion
to 2b
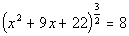
|
The base with the rational exponent is already isolated. |
If you raise an expression that has a rational exponent to the reciprocal
of that rational exponent, the exponent will disappear. This
is what we want to do here so that we can get x out from under the rational exponent and continue to solve for it. |
|
*Inverse of taking it to the 3/2 power is
taking it to the 2/3 power
*Use def.
of rat. exp
|
Step 3: Solve
the remaining equation. |
In this example, the equation that resulted from squaring both sides
turned out to be a quadratic equation.
If you need a review on solving quadratic equations, feel free to go
to Tutorial 17: Quadratic Equations. |
Let's check to see if x = -6 is an extraneous
solution: |
|
*Plugging in -6 for x
*True statement |
Since we got a true statement, x = -6
is a solution. |
Lets check to see if x = -3 is an extraneous
solution: |
|
*Plugging in -3 for x
*True statement |
Since we got a true statement, x = -3
is a solution.
There are two solutions to this rational exponent equation: x = -6 and x = -3. |

|
|


