College Algebra
Tutorial 19: Radical Equations andEquations Involving Rational Exponents
WTAMU > Virtual Math Lab > College Algebra
 Learning Objectives Learning Objectives
After completing this tutorial, you should be able to:
- Solve radical equations.
- Solve equations that have rational exponents.
|
 Introduction Introduction
In this tutorial, we will be looking at solving two different types
of equations, radical equations and equations that have rational exponents.
Both of these equations have the same ultimate goal, to get your variable
on one side and everything else on the other side using inverse operations.
Also, after removing the radical or rational exponent in the equations
in this tutorial, they become either a linear or quadratic equation.
Good news and bad news, as mentioned in other tutorials, a lot of
times in math you use previous knowledge to help work the new concepts.
That is good because you do not have to approach the problem as totally
new and learn all new steps. That can be overwhelming. It is
bad because you do have to remember things from the past. Sometimes
we condition ourselves to drain our brains after taking a test and sometimes
forget what we have learned. If you need a review on radicals in
general, feel free to go to Tutorial
4: Radicals. If you need a review on rational exponents in
general, feel free to go to Tutorial
5: Rational Exponents. If you need a review on solving linear
equations, feel free to go to Tutorial
14: Linear Equations in One Variable. If you need a review
on solving quadratic equations, feel free to go to Tutorial
17: Quadratic Equations. After going through this page,
you should be an old pro at working with roots. I think you are ready
to tackle these equations. |
 Tutorial Tutorial
|
Solving Radical Equations
|
Step 1: Isolate
one of the radicals.
In other words, get one radical on one side and everything else on the
other using inverse operations.
In some problems there is only one radical. However, there are
some problems that have more than one radical. In these problems
make sure you isolate just one. |
Step 2: Get rid
of your radical sign.
The inverse operation to a radical or a root is to raise it to an exponent.
Which exponent? Good question, it would be the exponent that matches
the index or root number on your radical.
In other words, if you had a square root, you would have to square it
to get rid of it. If you had a cube root, you would have to cube
it to get rid of it, and so forth.
You can raise both sides to the 2nd power, 10th power, hundredth power,
etc. As long as you do the same thing to both sides of the equation,
the two sides will remain equal to each other. |
Step 3: If you
still have a radical sign left, repeat steps 1 and 2.
Sometimes you start out with two or more radicals in your equation.
If that is the case and you have at least one nonradical term, you will
probably have to repeat steps 1 and 2. |
Step 4: Solve the
remaining equation.
Step 5: Check
for extraneous solutions.
When solving radical equations, extra solutions may come up when you
raise both sides to an even power. These extra solutions are called
extraneous solutions. If a value is an extraneous
solution, it is not a solution to the original problem.
In radical equations, you check for extraneous solutions by plugging
in the values you found back into the original problem. If the left side
does not equal the right side, then you have an extraneous solution. |
|
The radical in this equation is already isolated. |
If you square a square root, it will disappear. This is what
we want to do here so that we can get x out
from under the square root and continue to solve for it. |
|
*Inverse of taking the sq. root is squaring
it |
Step 3: If you
still have a radical left, repeat steps 1 and 2. |
No more radicals exist, so we do not have to repeat steps 1 and 2. |
Step 4: Solve
the remaining equation. |
|
*Inverse of add. 5 is sub. 5
*Inverse of mult. by 2 is div. by 2
|
Let's check to see if x = 22 is an extraneous
solution: |
|
*Plugging in 22 for x
*True statement |
Since we got a true statement, x = 22
is not an extraneous solution.
There is one solution to this radical equation: x = 22. |
|
*Inverse of add. x is sub. x
*Square root is by itself on one side of eq. |
If you square a square root, it will disappear. This is what
we want to do here so that we can get x out
from under the square root and continue to solve for it. |
Be careful on this one. It
is VERY TEMPTING to square the left side term by term and get 9 - x squared or 9 + x squared. However, you
need to square it as a side as shown above. Recall that when you
square a binomial you get the first term squared minus twice the product
of the two terms plus the second term squared. If you need a review
on squaring a binomial, feel free to go to Tutorial
6: Polynomials. |
Step 3: If you
still have a radical left, repeat steps 1 and 2. |
No more radicals exist, so we do not have to repeat steps 1 and 2. |
Step 4: Solve
the remaining equation. |
In this example, the equation that resulted from squaring both sides
turned out to be a quadratic equation.
If you need a review on solving quadratic equations, feel free to go
to Tutorial 17: Quadratic Equations. |
Let's check to see if x = 6 is an extraneous
solution: |
|
*Plugging in 6 for x
*False statement |
Since we got a false statement, x =
6 is an extraneous solution. |
Lets check to see if x = 2 is an extraneous
solution: |
|
*Plugging in 2 for x
*True statement |
Since we got a true statement, x = 2 is
a solution.
There is only one solution to this radical equation: x = 2. |
|
*Inverse of sub. sq. root is add. sq.
root
*One square root is by itself on one side of
eq. |
If you square a square root, it will disappear. This is what
we want to do here so that we can get y out
from under the square root and continue to solve for it. |
|
*Inverse of taking the sq. root is squaring
it
*Right side is a binomial
squared
|
Be careful on this one. It
is VERY TEMPTING to square the right side term by term and get 1
+ ( y + 1). However, you need to square
it as a side as shown above. Recall that when you square a binomial
you get the first term squared plus twice the product of the two terms
plus the second term squared. If you need a review on squaring a
binomial, feel free to go to Tutorial
6: Polynomials. |
Step 3: If you
still have a radical left, repeat steps 1 and 2. |
|
*Inverse of add. y and 2 is sub. y and 2
*Square root is by itself on one side of eq.
*Inverse of taking the sq. root is squaring
it
*Left side is a binomial
squared
|
Be careful on this one. It
is VERY TEMPTING to square the left side term by term and get y squared
plus 1. However, you need to square it as a side as shown above.
Recall that when you square a binomial you get the first term squared plus
twice the product of the two terms plus the second term squared.
If you need a review on squaring a binomial, feel free to go to Tutorial
6: Polynomials. |
Step 4: Solve
the remaining equation. |
In this example, the equation that resulted from squaring both sides
turned out to be a quadratic equation.
If you need a review on solving quadratic equations, feel free to go
to Tutorial 17: Quadratic Equations. |
Let's check to see if y = 3 is an extraneous
solution: |
|
*Plugging in 3 for y
*True statement |
Since we got a true statement, y = 3
is a solution. |
Let's check to see if y = -1 is an extraneous
solution: |
|
*Plugging in -1 for y
*True statement |
Since we got a true statement, y = -1
is a solution.
There are two solutions to this radical equation: y = 3 and y = -1. |
|
Solving Equations that have a
Rational Exponent
AND can be written in the form
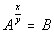
where B is any real number.
|
Step 1: Isolate
the base with the rational exponent.
In other words get the base with the rational exponent on one side
and everything else on the other using inverse operations. |
Step 2: Get rid
of the rational exponent.
The inverse operation to a rational exponent is to raise it to the
reciprocal of that exponent.
This will get rid of the rational exponent on the expression.
For example, if the rational exponent is 2/3, then the inverse operation
is to raise both sides to the 3/2 power.
You can raise both sides to ANY power. As long as you do the same
thing to both sides of the equation, the two sides will remain equal to
each other. |
Step 3: Solve the
remaining equation.
Step 4: Check
for extraneous solutions.
When solving equations with rational exponents, extra solutions may
come up when you raise both sides to an even power. These extra solutions
are called extraneous solutions. If a value
is an extraneous solution, it is not a solution to the original problem.
In equations with rational exponents you check for extraneous solutions
by plugging in the values you found back into the original problem. If
the left side does not equal the right side than you have an extraneous
solution. |
|
The base with the rational exponent is already isolated. |
If you raise an expression that has a rational exponent to the reciprocal
of that rational exponent, the exponent will disappear. This
is what we want to do here so that we can get x out from under the rational exponent and continue to solve for it. |
|
*Inverse of taking it to the 3/2 power
is
taking it to the 2/3 power
*Use def.
of rat. exp
|
Step 3: Solve
the remaining equation. |
In this example the equation that resulted from raising both sides
to the 2/3 power turned out to be a linear equation.
If you need a review on solving linear equations, feel free to go to Tutorial
14: Linear Equations in One Variable. |
|
*Inverse of add. 1 is sub. 1
*Inverse of mult. by 3 is div. by 3
|
Let's check to see if x = 5 is an extraneous
solution: |
|
*Plugging in 5 for x
*True statement |
Since we got a true statement, x = 5
is a solution.
There is one solution to this rational exponent equation: x = 5. |
|
*Inverse of sub. 10 is add. 10
*Inverse of mult. by 2 is div. by 2
*rat. exp. expression is by itself on one side
of eq. |
If you raise an expression that has a rational exponent to the reciprocal
of that rational exponent, the exponent will disappear. This
is what we want to do here so that we can get x out from under the rational exponent and continue to solve for it. |
|
*Inverse of taking it to the 5/3 power
is taking it to the 3/5 power
|
Step 3: Solve
the remaining equation. |
In this example, the equation that resulted from raising both sides
to the 3/5 power turned out to be a linear equation.
Also note that it is already solved for x.
So, we do not have to do anything on this step for this example. |
Let's check to see if 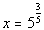 is an extraneous solution: is an extraneous solution: |
|
*Plugging in 5 to the 3/5 power for x
*True statement |
Since we got a true statement, 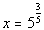 is a solution. is a solution.
There is one solution to this rational exponent equation: 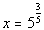 . . |
|
*Inverse of add. 1 is sub. 1
*rat. exp. expression is by itself on one side
of eq. |
If you raise an expression that has a rational exponent to the reciprocal
of that rational exponent, the exponent will disappear. This
is what we want to do here so that we can get x out from under the rational exponent and continue to solve for it. |
|
*Inverse of taking it to the 5/2 power
is
taking it to the 2/5 power
*The 5th root of -1 is -1 and -1 squared is
1. |
Step 3: Solve
the remaining equation. |
In this example, the equation that resulted from squaring both sides
turned out to be a quadratic equation.
If you need a review on solving quadratic equations, feel free to go
to Tutorial 17: Quadratic Equations. |
Lets check to see if x = -4 is an extraneous
solution: |
|
*Plugging in -4 for x
*False statement |
Since we got a false statement, x =
-4 is an extraneous solution. |
Let's check to see if x = -1 is an extraneous
solution: |
|
*Plugging in -1 for x
*False statement |
Since we got a false statement, x =
-1 is an extraneous solution.
There is no solution to this rational exponent equation. |
 Practice Problems Practice Problems
These are practice problems to help bring you to the next level.
It will allow you to check and see if you have an understanding of these
types of problems. Math works just like anything
else, if you want to get good at it, then you need to practice it.
Even the best athletes and musicians had help along the way and lots of
practice, practice, practice, to get good at their sport or instrument.
In fact there is no such thing as too much practice. To get the most out of these, you should work the problem out on
your own and then check your answer by clicking on the link for the answer/discussion
for that problem. At the link you will find the answer
as well as any steps that went into finding that answer. |
 Practice
Problems 1a - 1b: Solve each radical equation. Practice
Problems 1a - 1b: Solve each radical equation.
 Practice
Problems 2a - 2b: Solve each rational exponent equation. Practice
Problems 2a - 2b: Solve each rational exponent equation.
 Need Extra Help on these Topics? Need Extra Help on these Topics?

WTAMU > Virtual Math Lab > College Algebra
Videos at this site were created and produced by Kim Seward and Virginia Williams Trice.
Last revised on Dec. 16, 2009 by Kim Seward.
All contents copyright (C) 2002 - 2010, WTAMU and Kim Seward.
All rights reserved.
|
|


