

![]()
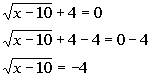
*Square root is by itself on one side of eq.
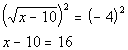
If you need a review on solving linear equations, feel free to go to Tutorial
14: Linear Equations in One Variable.
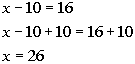
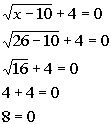
*False statement
There is no solution to this radical equation.
![]()
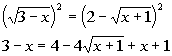
*Right side is a binomial
squared
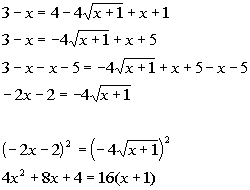
*Square root is by itself on one side of eq.
*Inverse of taking the sq. root is squaring
it
*Left side is a binomial
squared
If you need a review on solving quadratic equations feel free to go
to Tutorial 17: Quadratic Equations.
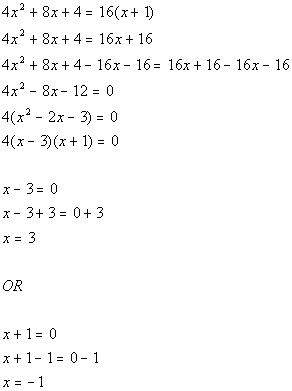
*Quad. eq. in standard form
*Factor
out a GCF of 4
*Factor
the trinomial
*Use Zero-Product
Principle
*Set 1st factor = 0 and solve
*Set 2nd factor = 0 and solve
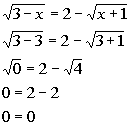
*True statement
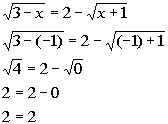
*True statement
There are two solutions to this radical equation: x = 3 and x = -1.
![]()
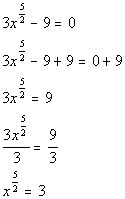
*Inverse of mult. by 3 is div. by 3
*rat. exp. expression is by itself on one side
of eq.
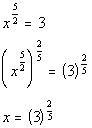
Also note that it is already solved for x.
So, we do not have to do anything on this step for this example.
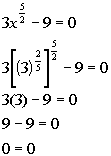
*Plugging in 3 to the 2/5 power for x
*True statement
There is one solution to this rational exponent equation: ![]() .
.
![]()
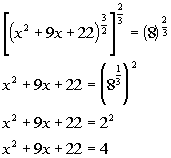
*Use def.
of rat. exp
If you need a review on solving quadratic equations, feel free to go
to Tutorial 17: Quadratic Equations.
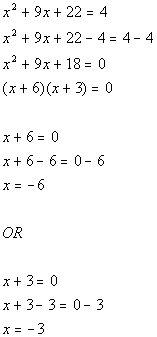
*Quad. eq. in standard form
*Factor
the trinomial
*Use Zero-Product
Principle
*Set 1st factor = 0 and solve
*Set 2nd factor = 0 and solve
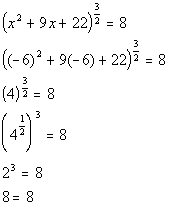
*Plugging in -6 for x
*True statement
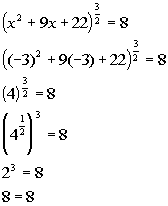
*True statement
There are two solutions to this rational exponent equation: x = -6 and x = -3.
Last revised on Dec. 16, 2009 by Kim Seward.
All contents copyright (C) 2002 - 2010, WTAMU and Kim Seward.
All rights reserved.