College Algebra
Tutorial 5: Rational Exponents
 Learning Objectives
After completing this tutorial, you should be able to:
- Rewrite a rational exponent in radical notation.
- Simplify an expression that contains a rational exponent.
- Use rational exponents to simplify a radical expression.
|
Introduction
In this tutorial we are going to combine two ideas that have been discussed
in earlier tutorials: exponents and radicals. We will look at how
to rewrite, simplify and evaluate these expressions that contain rational
exponents. What it boils down to is if you have a denominator
in your exponent, it is your index or root number.
So, if you need to, review radicals
covered in Tutorial 4: Radicals. Also, since we are working
with fractional exponents and they follow the exact same rules as integer
exponents, you will need to be familiar with adding, subtracting, and multiplying
them.
If you feel that you need a review, click on review
of fractions. To review exponents, you can go to Tutorial
2: Integer Exponents. Let's move onto rational exponents
and roots. |
Tutorial
|
Rational Exponents and Roots
If x is positive, p and q are
integers and q is positive,
|
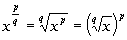
In other words, when you have a rational exponent, the denominator
of that exponent is your index or root number and the numerator of the
exponent is the exponential part.
I have found it easier to think of it in two parts. Find the root
part first and then take it to the exponential part if possible.
It makes the numbers a lot easier to work with.
Radical exponents follow the exact same exponent rules as discussed
in Tutorial 2: Integer Exponents. In that tutorial we only dealt with integers, but you can extend those
rules to rational exponents.
Here is a quick review of those exponential rules: |
Review of Exponential Rules
|
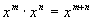
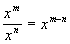
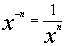
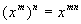
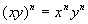
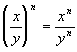
We are looking for the square root of 49 raised to the 1 power, which
is the same as just saying the square root of 49.
If your exponent's numerator is 1, you are basically just looking for
the root (the denominator's exponent).
Our answer is 7 since the square root of 49 is 7. |
In this problem we are looking for the cube root of -125 squared.
Again, I think it is easier to do the root part first if possible.
The numbers will be easier to work with.
The cube root of -125 is -5 and (-5) squared is 25. |
In this problem we have a negative exponent to start with. That means we need to take the reciprocal of the base. Note that we DO NOT take the reciprocal of the
exponent, only the base.
From there we are looking for the square root of 49/36 cubed.
Again, I think it is easier to do the root part first if possible.
The numbers will be easier to work with.
The square root of 49/36 is 7/6 and 7/6 cubed is 343/216. |
Practice Problems
These are practice problems to help bring you to the next level.
It will allow you to check and see if you have an understanding of these
types of problems. Math works just like anything
else, if you want to get good at it, then you need to practice it.
Even the best athletes and musicians had help along the way and lots of
practice, practice, practice, to get good at their sport or instrument.
In fact there is no such thing as too much practice. To get the most out of these, you should work the problem out on
your own and then check your answer by clicking on the link for the answer/discussion
for that problem. At the link you will find the answer
as well as any steps that went into finding that answer. |
 Practice
Problems 1a - 1b: Evaluate the expression.
Practice
Problems 2a - 2c: Simplify the expression.
Practice
Problem 3a: Simplify the expression by reducing the index of the radical. x represents positive real numbers.
Need Extra Help on these Topics?
Videos at this site were created and produced by Kim Seward and Virginia Williams Trice.
Last revised on Dec. 6, 2009 by Kim Seward.
All contents copyright (C) 2002 - 2010, WTAMU and Kim Seward.
All rights reserved.
|
|
Example
1: Evaluate 
.
.
.
.
.
.
by
reducing the index of the radical. 
