College Algebra
Tutorial 4: Radicals
 Learning Objectives Learning Objectives
After completing this tutorial, you should be able to:
- Find the principal nth root of an expression.
- Find the nth root of an expression raised to the nth power.
- Simplify radical expressions.
- Multiply radicals that have the same index number.
- Divide radicals that have the same index number.
- Add and subtract like radicals.
- Rationalize one term denominators of rational expressions.
- Rationalize two term denominators of rational expressions.
|
 Introduction Introduction
In this tutorial we will be looking at radicals (or
roots). Basically,
the root of an expression is the reverse of raising it to a
power.
For example, if you want the square root of an expression, then you
want
another expression, such that, when you square it, you get what is
inside
the square root. This concept carries through to all roots. We
will
be looking at rewriting, simplifying, adding, subtracting, multiplying,
and rationalizing the denominator of radicals. You never know
when your radical simplifying skills may come in handy, so you want to
be prepared. |
 Tutorial Tutorial
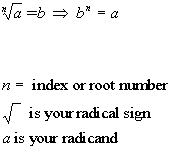
If n is even:
If n is even,
then a and b must be nonnegative for the root
to be
a real number.
If n is even and a is
negative, then the root is not a real number. |
If n is odd:
If n is odd, then a and b can be any real number. |
|
Things to note about radicals
in general:
When looking for the nth radical or nth root,
you want the expression
that, when you raise it to the nth power, you would get the radicand (what is inside the radical sign).
When there is no index number, n, it
is understood to be a 2 or square root. For example:
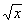 = principal square
root of x. = principal square
root of x.
Note that NOT EVERY RADICAL is a square root.
If there
is an index number n other than the
number
2, then you have a root other than a square root.
|
|
The thought behind this is that we are looking for the
square root
of 100. This means that we are looking for a number that when we square
it, we get 100.
What do you think it is?
Let’s find out if you are right:
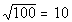
Since 10 squared is 100, 10 is the square root of
100.
Note that we are only interested in the principal root
and since 100
is positive and there is not a sign in front of the radical, our answer
is positive 10. If there had been a negative in front of the
radical
our answer would have been -10. |
Now we are looking for the negative of the fourth root
of 16, which
means we are looking for a number that when we raise it to the fourth
power
we get 16 (then we will take its negative).
What do you think it is?
Let’s find out if you are right:
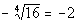
Since 2 raised to the fourth power is 16 and we are
negating that, our
answer is going to be -2.
Note that the negative was on the outside of our even
radical.
If the negative had been on the inside of an even radical, then the
answer
would be no real number. |
Now we are looking for the square root of -100, which
means we are
looking for a number that when we square it we get -100.
What do you think it is?
Let’s find out if you are right:
Since there is no such real number that when we square
it we get -100, the
answer is not a real number. |
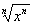 rule rule
If n is an even positive
integer, then 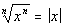
If n is an odd positive
integer, then 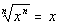
|
If a problem does not indicate that a variable is
positive, then
you need to assume that we are dealing with both positive and negative
real numbers and use this rule. |
Since it didn’t say that y is
positive,
we have to assume that it can be either positive or negative. And
since the root number and exponent are equal, then we can use the 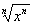 rule.
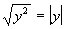
Since the root number and the exponent inside are equal
and are the
even number 2, we need to put an absolute value around y for our answer.
The reason for the absolute value is that we do not know
if y is positive or negative. So if we put y as our answer and it was negative, it would not be a true
statement.
For example if y was -5,
then -5 squared
would be 25 and the square root of 25 is 5, which is not the same as
-5.
The only time that you do not need the absolute value on a problem like
this is if it stated that the variable is positive. |
Since the root number and exponent are equal, then we
can use the 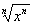 rule.
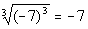
This time our root number and exponent were both the odd
number 3.
When an odd numbered root and exponent match then the answer is the
base
whether it is negative or positive. |
|
Simplifying a Radical Expression
|
When you simplify a radical, you want to take out as
much as possible.
We can use the product rule of
radicals (found
below) in reverse to help us simplify the nth root of a number that we
cannot take the nth root of as is, but has a factor that we can take
the
nth root of. If there is such a factor, we write the radicand as
the product of that factor times the appropriate number and
proceed.
We can also use the quotient rule of
radicals (found below) to simplify a fraction that we have under the radical.
Note that the phrase "perfect
square" means
that you can take the square root of it. Just as "perfect
cube" means we can take the cube root of the number, and so forth. I will be using that phrase in some of the following examples. |
A Product of Two Radicals
With the Same Index Number
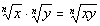
|
In other words, when you are multiplying two
radicals that have
the same index number, you can write the product under the same radical
with the common index number.
Note that if you have different index numbers, you
CANNOT multiply them
together.
Also, note that you can use
this rule in either
direction depending on what your problem is asking you to do. |
Note that both radicals have an index number of 3, so
we were able
to put their product together under one radical keeping the 3 as its
index
number.
Since we cannot take the cube root of 15 and 15 does not
have any factors
we can take the cube root of, this is as simplified as it gets. |
Note that both radicals have an index number of 4, so
we were able
to put their product together under one radical keeping the 4 as its
index
number.
Since we cannot take the fourth root of what is inside
the radical sign
and 24 does not have any factors we can take the fourth root of, this
is
as simplified as it gets. |
Even though 75 is not a perfect square, it does have a
factor that
we can take the square root of.
Check it out: |
In this example, we are using the product rule of
radicals in reverse
to help us simplify the square root of 75. When you simplify a
radical,
you want to take out as much as possible. The factor of 75 that
we
can take the square root of is 25. We can write 75 as (25)(3) and
then use the product rule of radicals to separate the two
numbers.
We can take the square root of the 25 which is 5, but we will have to
leave
the 3 under the square root. |
Even though 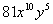
is not a perfect cube, it does have a factor that we can take the cube
root of. Check it out: |
In this example, we are using the product rule of
radicals in reverse
to help us simplify the cube root of 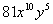 .
When you simplify a radical, you want to take out as much as
possible.
The factor of 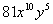 that we can take the cube root of is 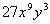 . We can write 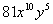 as 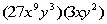 and then use the product rule of radicals to separate the two
numbers.
We can take the cube root of 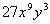 ,
which is 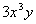 ,
but
we will have to leave the rest of it under the cube root. |
A Quotient of Two Radicals
With the Same Index Number
If n is even, x and y represent
any nonnegative real number and y does not equal 0.
If n is odd, x and y represent
any real number and y does not equal 0.
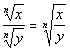
|
This works in the same fashion as the rule for a
product of two radicals.
This rule can also work in either direction. |
|
*The cube root of -1 is -1 and
the cube root
of 27 is 3
|
Since we cannot take the square root of 10 and 10 does
not have any
factors that we can take the square root of, this is as simplified as
it
gets. |
Like radicals are radicals that have the same root
number AND radicand
(expression under the root).
The following are two examples of two different pairs of
like radicals:
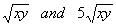
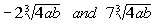
|
Adding and Subtracting
Radical Expressions
|
Step 2: Combine like
radicals.
You can only add or subtract radicals together if
they are like
radicals.
You add or subtract them in the same fashion that
you do like terms.
Combine the numbers that are in front of the like radicals and write
that
number in front of the like radical part. |
|
Both radicals are as simplified as it gets. |
Step 2: Combine like
radicals. |
Note how both radicals are the cube root of 2.
These two radicals
are like radicals. |
|
*Combine like radicals: 3x + 7x = 10x |
The 75 in the second radical has a factor that we can
take the square
root of.
Can you think of what that factor is?
Let’s see what we get when we simplify the second
radical: |
The first radical is already in its simplest form. |
Step 2: Combine like
radicals. |
|
*Combine like radicals: 4 - 30
= -26 |
Rationalizing the
Denominator
(with one term)
|
When a radical contains an expression that is not a
perfect root,
for example, the square root of 3 or cube root of 5, it is called
an irrational number. So, in order to rationalize the
denominator,
we need to get rid of all radicals that are in the denominator. |
Step 1: Multiply
numerator
and denominator by a radical that will get rid of the radical in the
denominator. |
If the radical in the denominator is a square root,
then you multiply
by a square root that will give you a perfect square under the radical
when multiplied by the denominator. If the radical in the
denominator
is a cube root, then you multiply by a cube root that will give you a
perfect
cube under the radical when multiplied by the denominator and so
forth...
Note that the phrase "perfect
square" means
that you can take the square root of it. Just as "perfect
cube" means we can take the cube root of the number, and so
forth.
Keep in mind that as long as you multiply the numerator
and denominator
by the exact same thing, the fractions will be equivalent. |
Step 3: Simplify
the
fraction if needed. |
Be careful. You cannot cancel out a factor that
is on the outside
of a radical with one that is on the inside of the radical. In
order
to cancel out common factors, they have to be both inside the same
radical
or be both outside the radical. |
Step 1: Multiply numerator
and denominator by a radical that will get rid of the radical in the
denominator. |
Since we have a square root in the denominator, then we need to
multiply by the square root of an expression that will give us a
perfect
square under the radical in the denominator.
Square roots are nice to work with in this type of
problem because if
the radicand is not a perfect square to begin with, we just have to
multiply
it by itself and then we have a perfect square.
So in this case we can accomplish this by multiplying
top and bottom
by the square root of 5: |
|
*Mult. num. and den. by sq. root
of 5
*Den. now has a perfect square
under sq. root
|
Step 3: Simplify the
fraction if needed. |
Be careful when you reduce a fraction like
this. It is
real tempting to cancel the 5 which is on the outside of the radical
with
the 5 which is inside the radical on the last fraction. You
cannot
do that unless they are both inside the same radical or both outside
the
radical. |
Step 1: Multiply
numerator
and denominator by a radical that will get rid of the radical in the
denominator. |
Since we have a cube root in the denominator, we
need to multiply
by the cube root of an expression that will give us a perfect cube
under
the radical in the denominator.
So in this case, we can accomplish this by
multiplying top and bottom
by the cube root of 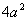 : : |
|
*Mult. num. and den. by cube
root of 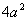
*Den. now has a perfect cube
under cube root
|
Step 3: Simplify the
fraction if needed. |
|
*Cube root of 8 a cube is 2a
|
As discussed in example 14, we would not be able to
cancel out the
2 with the 20 in our final fraction because the 2 is on the outside of
the radical and the 20 is on the inside of the radical.
Also, we cannot take the cube root of anything under the
radical.
So, the answer we have is as simplified as we can get it. |
Rationalizing the
Denominator
(with two terms)
|
Above we talked about rationalizing the denominator
with one term.
Again, rationalizing the denominator means to get rid of any radicals
in
the denominator.
Because we now have two terms, we are going to have to
approach it differently
than when we had one term, but the goal is still the same. |
Step 1:
Find the conjugate
of the denominator. |
You find the conjugate of a binomial by changing the
sign that is between
the two terms, but keep the same order of the terms.
a + b and a - b are conjugates
of each other. |
Step 2: Multiply the
numerator and the denominator of the fraction by the conjugate found in
Step 1. |
Keep in mind that as long as you multiply the numerator
and denominator
by the exact same thing, the fractions will be equivalent.
When you multiply conjugates
together you get:
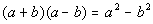
|
Step 4: Simplify the
fraction if needed. |
Be careful. You cannot cancel out a factor that
is on the outside
of a radical with one that is on the inside of the radical. In
order
to cancel out common factors, they have to be both inside the same
radical
or be both outside the radical. |
Step 1: Find the conjugate
of the denominator. |
In general the conjugate of a + b is a - b and vice versa.
So what would the conjugate of our denominator be?
It looks like the conjugate is 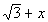 . . |
Step 2: Multiply the
numerator and the denominator of the fraction by the conjugate found in
Step 1. |
|
*Mult. num. and den. by conjugate
of den.
*Use distributive prop. to
multiply the numerators
*In general, product of conjugates
is 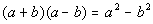
|
Step 4: Simplify the
fraction if needed. |
|
*Square root of 3 squared is 3
|
Step 1: Find the conjugate
of the denominator. |
In general the conjugate of a + b is a - b and vice versa.
So what would the conjugate of our denominator be?
It looks like the conjugate is 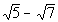 . . |
Step 2: Multiply the
numerator and the denominator of the fraction by the conjugate found in
Step 1. |
|
*Mult. num. and den. by conjugate
of den.
*Use distributive prop. to
multiply the numerators
*In general, product of conjugates
is 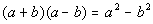
|
Step 4: Simplify the
fraction if needed. |
|
*Square root of 5 squared is 5
*Square root of 7 squared is 7
*Divide BOTH terms of num. by -2
|
 Practice Problems Practice Problems
These are practice problems to help bring you to the
next level.
It will allow you to check and see if you have an understanding of
these
types of problems. Math works just like
anything
else, if you want to get good at it, then you need to practice
it.
Even the best athletes and musicians had help along the way and lots of
practice, practice, practice, to get good at their sport or instrument.
In fact there is no such thing as too much practice. To get the most out of these, you should work the
problem out on
your own and then check your answer by clicking on the link for the
answer/discussion
for that problem. At the link you will find the answer
as well as any steps that went into finding that answer. |
 Practice
Problems 1a - 1d: Evaluate or indicate that the root is
not a real number. Practice
Problems 1a - 1d: Evaluate or indicate that the root is
not a real number.
 Practice
Problems 2a - 2b: Use the product rule to simplify the
expression. Practice
Problems 2a - 2b: Use the product rule to simplify the
expression.
 Practice
Problems 3a - 3b: Use the quotient rule to simplify the
expression Practice
Problems 3a - 3b: Use the quotient rule to simplify the
expression
 Practice
Problems 4a - 4b: Add or subtract. Practice
Problems 4a - 4b: Add or subtract.
 Practice
Problems 5a - 5b: Rationalize the denominator. Practice
Problems 5a - 5b: Rationalize the denominator.
 Need Extra Help on these Topics? Need Extra Help on these Topics?

Videos at this site were created and produced by Kim Seward and Virginia Williams Trice.
Last revised on Dec. 6, 2009 by Kim Seward.
All contents copyright (C) 2002 - 2010, WTAMU and Kim Seward. All rights reserved.
|
|


