In this example, we are using the product rule of radicals in reverse
to help us simplify the cube root of
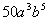
.
When you simplify a radical, you want to take out as much as possible.
The factor of
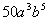
that we can take the square root of is
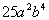
. We can write
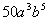
as
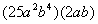
and then use the product rule of radicals to separate the two numbers.
We can take the square root of
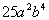
,
which is
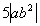
, but
we will have to leave the rest of it under the square root.


