College Algebra
Tutorial 17: Quadratic Equations
WTAMU > Virtual Math Lab > College Algebra
 Learning Objectives Learning Objectives
After completing this tutorial, you should be able to:
- Solve quadratic equations by factoring.
- Solve quadratic equations by the square root method.
- Solve quadratic equations by completing the square.
- Solve quadratic equations by using the quadratic
formula.
- Find the discriminant of a quadratic equation and use
it to tell how
many
and what type of solutions the equation has.
|
 Introduction Introduction
In this tutorial, we will be looking at solving a
specific type of
equation called the quadratic equation. The methods of solving
these
types of equations that we will take a look at are solving by
factoring,
by using the square root method, by completing the square, and by using
the quadratic equation. Sometimes one method won't work or
another
is just faster, depending on the quadratic equation given. So it
is good to know different ways to solve quadratic equations so you will
be prepared for any type of situation. After completing
this
tutorial, you will be a master at solving quadratic equations.
Solving
equations in general is a very essential part of Algebra. So I
guess
we better get to it. |
 Tutorial Tutorial
Quadratic Equation
Standard form:
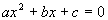 , ,
Where a does not equal 0.
|
|
Note that the difference is the highest exponent on the
variable on
the quadratic equation is 2.
We are going to talk about four ways to solve quadratics. |
|
Solving Quadratic Equations
by Factoring
|
You can solve
a quadratic equation
by factoring if, after writing it in standard form, the quadratic
expression
factors.
Step 1: Simplify each
side if needed.
This would involve things like removing ( ),
removing fractions, adding
like terms, etc.
To remove ( ): Just use the
distributive property.
To remove fractions: Since fractions are
another way to write
division, and the inverse of divide is to multiply, you remove
fractions
by multiplying both sides by the LCD of all of your fractions. |
Step 2: Write in
standard form, 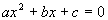 ,
if needed. ,
if needed.
If it is not in standard form, move any term(s)
to the appropriate
side by using the addition/subtraction property of equality.
Also, make sure that the squared term is written
first left to right,
the x term is second and the constant is
third
and it is set equal to 0. |
Step 3: Factor.
Step 4:
Use the
Zero-Product Principle.
If ab = 0, then a = 0 or b = 0.
0 is our magic number because the only way a
product can become 0
is if at least one of its factors is 0.
You can not guarantee what the factors would have
to be if the product
was set equal to any other number. For example if ab = 1, then a = 5 and b = 1/5 or a = 3 and b = 1/3, etc. But with the product set equal to 0, we can guarantee
finding the solution by setting each factor equal to 0. That is
why
it is important to get it in standard form to begin with. |
Step 5: Solve for the
linear equation(s) set up in step 4.
If a quadratic equation factors, it will factor
into either one linear
factor squared or two distinct linear factors. So, the equations
found in step 4 will be linear equations. If you need a review on
solving linear equations feel free to go to Tutorial
14: Linear Equations in One Variable. |
 Example
1: Solve Example
1: Solve 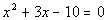 by factoring. by factoring.
 View a video of this example View a video of this example
|
This quadratic equation is already simplified. |
Step 2: Write
in standard form, 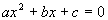 ,
if needed. ,
if needed. |
This quadratic equation is already in standard form. |
|
*Use Zero-Product Principle
*Solve the first linear equation
*Solve the second linear
equation
|
There are two solutions to this quadratic equation: x =
-5 and x = 2. |
|
*Mult. both sides by LCD of 6
to clear fractions
|
Step 2: Write
in standard form, 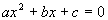 ,
if needed. ,
if needed. |
|
*Inverse of add. 16 is sub. 16
*Quad. eq. in standard form |
|
*Use Zero-Product Principle
*Solve the first linear equation
*Solve the second linear
equation
|
There are two solutions to this quadratic equation: x =
-4/5 and x = 4/5. |
|
*Use Dist. Prop. to clear the
( ) |
Step 2: Write
in standard form, 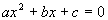 ,
if needed. ,
if needed. |
|
*Inverse of add. 2 is sub. 2
*Quad. eq. in standard form
|
|
*Use Zero-Product Principle
*Solve the first linear equation
*Solve the second linear
equation
|
There are two solutions to this quadratic equation: x =
-2/3 and x = 1/2. |
|
Solving Quadratic Equations by the Square Root Method
|
You can solve
a quadratic equation
by the square root method if you can write it in the form 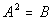 . .
Step 1: Write the
quadratic equation in the form 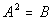 if
needed. if
needed.
A and B represent
algebraic expressions. When you have the quadratic equation
written
in this form, it allows you to use the square root method described in
step 2. If it is not in this form, 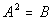 ,
move any term(s) to the appropriate side by using the
addition/subtraction
or multiplication/division property of equality. ,
move any term(s) to the appropriate side by using the
addition/subtraction
or multiplication/division property of equality. |
Step 2: Apply the
square root method.
If A and B are algebraic expressions such that 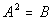 ,
then 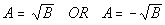 ,
also written 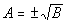 . .
In other words, if you have an expression squared
set equal to another
expression, the inverse operation to solve it is to take the square
root
of both sides. Since both a positive and its opposite squared
result
in the same answer, then you will have two answers, plus or minus the
square
root of B. |
Step 3: Solve for the
linear equation(s) set up in step 2.
After applying the square root method to a
quadratic equation you will
end up with either one or two linear equations to solve. Most
times
you will have two linear equations, but if B is equal to 0, then
you will only have one since plus or minus 0 is only one number.
If you need a review on solving linear equations feel free to go to Tutorial
14: Linear Equations in One Variable. |
 Example
4: Solve Example
4: Solve 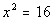 by using the square root method. by using the square root method.
 View a video of this example View a video of this example
|
|
*Written in the form 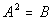 *Apply the sq. root method
*There are 2 solutions
*Apply the sq. root method
*There are 2 solutions |
Step 3: Solve for the
linear equation(s) set up in step 2. |
|
*Sq. root of 16 = 4
*Neg. sq. root of 16 = - 4
|
There are two solutions to this quadratic equation: x =
4 and x = -4. |
Note how this quadratic equation is not in the
form 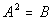 to begin with. The 5 is NOT part of the expression being squared
on the left side of the equation. We can easily write it in the
form 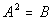 by dividing both sides by 5. |
|
*Not in the form 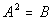 *Inv. of mult. by 5 is div. by 5
*Inv. of mult. by 5 is div. by 5
*Written in the form 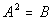
*Apply the sq. root method
*There are 2 solutions |
Step 3: Solve for the
linear equation(s) set up in step 2. |
|
*Sq. root of 4 = 2
*Neg. sq. root of 4 = -2
|
There are two solutions to this quadratic equation: x =
2 and x = -2. |
|
*Written in the form 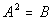
*Apply the sq. root method
*There are 2 solutions |
Step 3: Solve for the
linear equation(s) set up in step 2. |
|
*Sq. root of 20 = 2 sq. root of
5
*Solve for x
*Neg. sq. root of 20 = -2 sq.
root of 5
*Solve for x
|
There are two solutions to this quadratic equation: x = 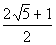 and x =
and x = 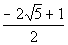 . . |
|
Solving Quadratic Equations by Completing the Square
|
You can solve
ANY quadratic
equation by completing the square. This comes in handy when a
quadratic
equation does not factor or is difficult to factor. |
Step 1: Make
sure that the coefficient on the 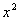 term is equal to 1. term is equal to 1. |
If the coefficient of the 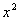 term is already 1, then proceed to step 2.
If the coefficient of the 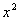 term is not equal to 1, then divide both sides by that coefficient. term is not equal to 1, then divide both sides by that coefficient. |
Step 2: Isolate
the 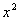 and x terms. and x terms. |
In other words, rewrite it so that the 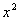 and x terms are on one side and the constant is on the other side. |
Step 3: Complete
the square. |
At this point we will be creating a perfect square
trinomial (PST).
Recall that a PST is a trinomial of the form 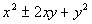 and
it factors in the form 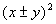 .
When it is in that form it will allow us to continue onto the next step
and take the square root of both sides and find a solution. We need to find a number that
we can add to
the 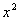 and x terms so that we have a PST. and x terms so that we have a PST.
We can get that magic number by
doing the following:
If we have
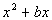
we can complete it’s
square by adding the constant
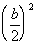
|
In other words, we complete the square by taking
½ of b (the coefficient of the x term) and then
squaring
it. Make sure you remember to add it to BOTH sides to keep the
equation
balanced. |
Step 4: Factor
the perfect square trinomial (created in step 3) as a binomial squared. |
The coefficient of the 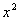 term is already 1. |
The 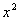 and x terms
are already isolated. |
|
*b is the coefficient of the x term
*Complete the square by taking
1/2 of b and squaring it
|
|
*Add constant found above to
BOTH sides of
the eq.
*This creates a PST on the left
side of eq. |
|
*Written in the form 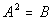 *Apply the sq. root method
*There are 2 solutions
*Apply the sq. root method
*There are 2 solutions
|
There are two solutions to this quadratic equation: x =
9 and x = 1. |
Note how the coefficient on the 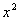 term is not 1 to begin with. We can easily fix that by dividing
both
sides by that coefficient, which in this case is 3 . |
|
*Divide both sides by 3
*Coefficient of 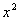 term is now 1 term is now 1
|
Note how the 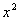 and x terms are not isolated to begin
with.
We can easily fix that by moving the constant to the other side of the
equation. |
|
*Inverse of add. 3 is sub. 3
*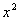 and x terms are now isolated and x terms are now isolated
|
|
*b is the coefficient of the x term
*Complete the square by taking
1/2 of b and squaring it
|
|
*Add constant found above to
BOTH sides of
the eq.
*This creates a PST on the left
side of eq.
|
There are two solutions to this quadratic equation: x = 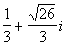 and x =
and x = 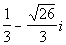 . . |
|
Solving Quadratic Equations by the Quadratic Formula
When 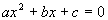 , then , then
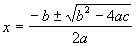
|
You can solve
ANY quadratic
equation by using the quadratic formula. This comes in handy when
a quadratic equation does not factor or is difficult to factor. |
Step 1: Simplify each
side if needed.
This would involve things like removing ( ),
removing fractions, adding
like terms, etc.
To remove ( ): Just use the
distributive property.
To remove fractions: Since fractions are
another way to write
division, and the inverse of divide is to multiply, you remove
fractions
by multiplying both sides by the LCD of all of your fractions. |
Step 2: Write in
standard form, 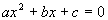 ,
if needed. ,
if needed.
If it is not in standard form, move any term(s)
to the appropriate
side by using the addition/subtraction property of equality.
Also, make sure that the squared term is written
first left to right,
the x term is second and the constant is
third
and it is set equal to 0. |
Step 3: Identify a, b,
and c.
When the quadratic equation is in standard
form, 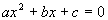 ,
then a is the coefficient in front of
the 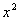 term, b is the coefficient in front of the x term,
and c is the constant term. |
Step 4: Plug the
values found in step 3 into the quadratic formula.
When 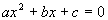 , then 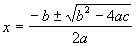
|
Step 5: Simplify if possible. |
This quadratic equation is already simplified. |
Step 2: Write
in standard form, 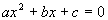 ,
if needed. ,
if needed. |
This quadratic equation is already in standard form. |
a, the number in
front of x squared, is 2.
b, the number in front
of x,
is -5.
c, the constant, is 1.
Make sure that you keep the sign that is in front of
each of these numbers.
Next we will plug it into the quadratic
formula. Note that
we are only plugging in numbers, we don't also plug in the variable. |
|
AND
Step 5: Simplify if possible. |
|
*Quadratic formula
*Plug in values found above for a, b,
and c
*Simplify
|
This quadratic equation is already simplified. |
Step 2: Write
in standard form, 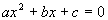 ,
if needed. ,
if needed. |
This quadratic equation is already in standard form. |
a, the number in
front of x squared, is 1.
b, the number in front
of x,
is 0.
Note that b is 0 because
the x term is missing.
c, the constant, is 9.
Make sure that you keep the sign that is in front of
each of these numbers.
Next we will plug it into the quadratic
formula. Note that
we are only plugging in numbers, we don't also plug in the variable. |
|
AND
Step 5: Simplify if possible. |
This quadratic equation is already simplified. |
Step 2: Write
in standard form, 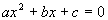 ,
if needed. ,
if needed. |
|
*Inverse of add. 6x is sub. 6x
*Quad. eq. in standard form |
a, the number in
front of x squared, is 1.
b, the number in front
of x,
is -6.
c, the constant, is 9.
Make sure that you keep the sign that is in front of
each of these numbers.
Next we will plug it into the quadratic
formula. Note that
we are only plugging in numbers, we don't also plug in the variable. |
|
AND
Step 5: Simplify if possible. |
|
*Quadratic formula
*Plug in values found above for a, b,
and c
*Simplify
|
When a quadratic equation is in standard form, 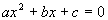 ,
the expression, ,
the expression, 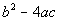 ,
that is found under the square root part of the quadratic formula is
called
the discriminant. ,
that is found under the square root part of the quadratic formula is
called
the discriminant.
The discriminant can tell you how many solutions there
are going to
be and if the solutions are real numbers or complex imaginary numbers. |
Step 1: Simplify each
side if needed.
This would involve things like removing ( ),
removing fractions, adding
like terms, etc.
To remove ( ): Just use the
distributive property.
To remove fractions: Since fractions are
another way to write
division, and the inverse of divide is to multiply, you remove
fractions
by multiplying both sides by the LCD of all of your fractions. |
Step 2: Write in
standard form, 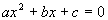 ,
if needed. ,
if needed.
If it is not in standard form, move any term(s)
to the appropriate
side by using the addition/subtraction property of equality.
Also, make sure that the squared term is written
first left to right,
the x term is second and the constant is
third
and it is set equal to 0. |
Step 3: Identify a, b,
and c.
When the quadratic equation is in standard
form, 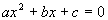 ,
then a is the coefficient in front of
the 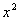 term, b is the coefficient in front of the x term,
and c is the constant term. |
Step 4: Plug the
values found in step 3 into the discriminant, 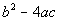 . .
Step 5: Simplify if possible. |
 Example
12: Find the discriminant. Based on the discriminant,
indicate how many and what type of solutions there would be. Example
12: Find the discriminant. Based on the discriminant,
indicate how many and what type of solutions there would be. 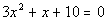
 View a video of this example View a video of this example
|
This quadratic equation is already simplified. |
Step 2: Write
in standard form, 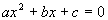 ,
if needed. ,
if needed. |
This quadratic equation is already in standard form. |
a, the number in
front of x squared, is 3.
b, the number in front
of x,
is 1.
c, the constant, is 10.
Make sure that you keep the sign that is in front of
each of these numbers. |
Step 4: Plug the
values found in step 3 into the discriminant, 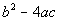 . .
AND
Step 5: Simplify if possible. |
|
*Discriminant formula
*Plug in values found above for a, b,
and c
*Discriminant |
Since the discriminant is a negative number, that
means there are
two distinct complex imaginary solutions. |
 Example
13: Find the discriminant. Based on the discriminant,
indicate how many and what type of solutions there would be. Example
13: Find the discriminant. Based on the discriminant,
indicate how many and what type of solutions there would be. 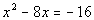 . .
 View a video of this example View a video of this example
|
This quadratic equation is already simplified. |
Step 2: Write
in standard form, 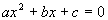 ,
if needed. ,
if needed. |
|
*Inverse of sub. 16 is add. 16
*Quad. eq. in standard form |
a, the number in
front of x squared, is 1.
b, the number in front
of x,
is -8.
c, the constant, is 16.
Make sure that you keep the sign that is in front of
each of these numbers. |
Step 4: Plug the
values found in step 3 into the discriminant, 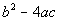 . .
AND
Step 5: Simplify if possible. |
|
*Discriminant formula
*Plug in values found above for a, b,
and c
*Discriminant |
Since the discriminant is zero, that means there is
only one real
number solution. |
 Example
14: Find the discriminant. Based on the discriminant,
indicate how many and what type of solutions there would be. Example
14: Find the discriminant. Based on the discriminant,
indicate how many and what type of solutions there would be. 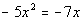 . .
 View a video of this example View a video of this example
|
This quadratic equation is already simplified. |
Step 2: Write
in standard form, 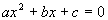 ,
if needed. ,
if needed. |
|
*Inverse of sub. 7x is add. 7x
*Quad. eq. in standard form |
a, the number in
front of x squared, is -5.
b, the number in front
of x,
is 7.
c, the constant, is 0.
Note that since the constant is missing it is understood
to be 0.
Make sure that you keep the sign that is in front of
each of these numbers. |
Step 4: Plug the
values found in step 3 into the discriminant, 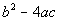 . .
AND
Step 5: Simplify if possible. |
|
*Discriminant formula
*Plug in values found above for a, b,
and c
*Discriminant |
Since the discriminant is a positive number, that
means there are
two distinct real number solutions. |
 Practice Problems Practice Problems
These are practice problems to help bring you to the
next level.
It will allow you to check and see if you have an understanding of
these
types of problems. Math works just like
anything
else, if you want to get good at it, then you need to practice
it.
Even the best athletes and musicians had help along the way and lots of
practice, practice, practice, to get good at their sport or instrument.
In fact there is no such thing as too much practice. To get the most out of these, you should work the
problem out on
your own and then check your answer by clicking on the link for the
answer/discussion
for that problem. At the link you will find the answer
as well as any steps that went into finding that answer. |
 Practice
Problems 1a - 1b: Solve by factoring. Practice
Problems 1a - 1b: Solve by factoring.
 Practice
Problems 2a - 2b: Solve by using the square root method. Practice
Problems 2a - 2b: Solve by using the square root method.
 Practice
Problems 3a - 3b: Solve by completing the square. Practice
Problems 3a - 3b: Solve by completing the square.
 Practice
Problems 4a - 4c: Solve by using the quadratic equation. Practice
Problems 4a - 4c: Solve by using the quadratic equation.
 Practice
Problems 5a - 5c: Find the discriminant. Based on the discriminate, indicate how
many and what
type of solutions there would be. Practice
Problems 5a - 5c: Find the discriminant. Based on the discriminate, indicate how
many and what
type of solutions there would be.
 Need Extra Help on these Topics? Need Extra Help on these Topics?

WTAMU > Virtual Math Lab > College Algebra
Videos at this site were created and produced by Kim Seward and Virginia Williams Trice.
Last revised on Dec. 17, 2009 by Kim Seward.
All contents copyright (C) 2002 - 2010, WTAMU and Kim Seward.
All rights reserved.
|
|


