College Algebra
Tutorial 7: Factoring Polynomials
 Learning Objectives Learning Objectives
After completing this tutorial, you should be able to:
- Find the Greatest Common Factor (GCF) of a polynomial.
- Factor out the GCF of a polynomial.
- Factor a polynomial with four terms by grouping.
- Factor a trinomial of the form
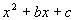 . .
- Factor a trinomial of the form
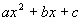 . .
- Indicate if a polynomial is a prime polynomial.
- Factor a perfect square trinomial.
- Factor a difference of squares.
- Factor a sum or difference of cubes.
- Apply the factoring strategy to factor a polynomial
completely.
|
 Introduction Introduction
Factoring is to write an expression as a product of
factors.
For example, we can write 10 as (5)(2), where 5 and 2 are called
factors
of 10. We can also do this with polynomial expressions. In
this tutorial we are going to look at several ways to factor polynomial
expressions. By the time I'm through with you, you will be a
factoring machine.
Basically, when we factor, we reverse the process of multiplying
the polynomial which was covered in Tutorial 6: Polynomials. |
|
 Tutorial Tutorial
|
Greatest Common Factor (GCF)
|
The GCF for a polynomial is the largest monomial
that divides (is
a factor of) each term of the polynomial. |
Step 1: Identify
the GCF of the polynomial.
Step 2:
Divide
the GCF out of every term of the polynomial.
This process is basically the reverse of the
distributive property. |
|
Step 1:
Identify
the GCF of the polynomial. |
The largest monomial that we can factor out of each
term is 2y. |
Step 2:
Divide
the GCF out of every term of the polynomial. |
|
*Divide 2y out
of every term of the poly.
|
Be careful. If a term
of the polynomial
is exactly the same as the GCF, when you divide it by the GCF you are
left
with 1, NOT 0. Don’t think, 'oh I have nothing left',
there is actually a 1. As shown above when we divide 2y by 2y we get 1, so we need a 1 as the
third
term inside of the ( ). Note that if we multiply our answer out, we should get
the original
polynomial. In this case, it does check out. Factoring
gives
you another way to write the expression so it will be equivalent to the
original problem. |
This problem looks a little different, because now our
GCF is a binomial.
That is ok, we treat it in the same manner that we do when we have a
monomial
GCF.
Note that this is not in factored form because of the
plus sign we have
before the 5 in the problem. To be in factored form, it must be
written
as a product of factors. |
Step 1:
Identify
the GCF of the polynomial. |
This time it isn't a monomial but a binomial that we
have in common.
Our GCF is (3x -1). |
Step 2:
Divide
the GCF out of every term of the polynomial. |
|
*Divide (3x -
1) out of both parts
|
When we divide out the (3x - 1) out of
the first term, we are left with x.
When
we divide it out of the second term, we are left with 5.
That is how we get the (x +
5) for our second
( ). |
Factoring a Polynomial with
Four Terms by Grouping
|
In some cases there is not a GCF for ALL the terms
in a polynomial.
If you have four terms with no GCF, then try factoring by grouping.
Step 1: Group
the first
two terms together and then the last two terms together.
Step 2: Factor out a GCF
from each separate binomial.
Step 3: Factor out the
common binomial. |
Note how there is not a GCF for ALL the terms. So
let’s go ahead
and factor this by grouping. |
Step 1: Group the first
two terms together and then the last two terms together. |
Step 2: Factor
out a
GCF from each separate binomial. |
|
*Factor out an x squared
from the 1st ( )
*Factor out a 2 from the 2nd
( ) |
Step 3: Factor out the
common binomial. |
|
*Divide (x + 3)
out of both parts
|
Note that if we multiply our answer out, we do get the
original polynomial. |
Note how there is not a GCF for ALL the terms. So
let’s go ahead
and factor this by grouping. |
Step 1: Group the first
two terms together and then the last two terms together. |
Be careful. When
the first
term of the second group of two has a minus sign in front of it, you
want
to put the minus in front of the second ( ). When you
do this you need to change the sign of BOTH terms of the second (
) as shown above. |
Step 2: Factor
out a
GCF from each separate binomial. |
|
*Factor out a 7x squared
from the 1st ( )
*Nothing to factor out from the
2nd (
) |
Step 3: Factor out the
common binomial. |
|
*Divide (x - 2)
out of both parts
|
Note that if we multiply our answer out that we do get
the original
polynomial. |
|
Factoring
Trinomials of
the Form
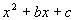
(Where the number in front of x squared is 1)
|
Basically, we are reversing the FOIL method to get
our factored
form. We are looking for two binomials that when you multiply
them
you get the given trinomial.
Step 1: Set up a product
of two ( ) where each will hold two terms.
It will look like this:
( )(
). |
Step 2: Find the factors
that go in the first positions.
To get the x squared (which is the F in
FOIL), we would have to have an x in
the first
positions in each ( ).
So it would look like this: (x
)(x ). |
Step 3: Find the
factors that go in the last positions.
The factors that would go in the last position
would have to be two
expressions such that their product equals c (the constant) and at the same time their sum equals b (number in front of x term).
As you are finding these factors, you have to
consider the sign of the
expressions:
If c is positive,
your factors are going to both have the same sign depending on b’s
sign. If c is negative,
your factors are going to have opposite signs depending on b’s
sign. |
|
|
Note that this trinomial does not have a GCF.
So we go right into factoring the trinomial of the
form 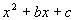 . . |
Step 1: Set
up a product
of two ( ) where each will hold two terms. |
It will look like
this:
(
)( ) |
Step 2: Find
the factors
that go in the first positions. |
Since we have a squared
as our first term,
we will need the following:
(a
)(a ) |
Step 3: Find
the
factors that go in the last positions. |
We need two numbers whose product is -14 and sum is
-5. That
would have to be -7 and 2.
Putting that into our factors we get: |
|
*-7 and 2 are two numbers whose
prod. is -14
and sum is -5
|
Note that if we would multiply this out, we would get
the original
trinomial. |
Note that this trinomial does have a GCF of 2y.
We need to factor out the GCF
before
we tackle the trinomial part of this. |
|
*Factor out the GCF of 2y
|
We are not finished, we can still factor the
trinomial. It is
of the form 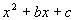 .
Anytime you are factoring, you need to make sure that
you factor everything
that is factorable. Sometimes you end up having to do several
steps
of factoring before you are done. |
Step 1
(trinomial): Set
up a product of two ( ) where each will hold two terms. |
It will look like this: 2y(
)( ) |
Step 2
(trinomial): Find
the factors that go in the first positions. |
Since we have x squared as our first term, we will need
the following:
2y(x
)(x ) |
Step 3
(trinomial): Find the factors that go in the last positions. |
We need two numbers whose product is 15 and sum is
8. That
would have to be 5 and 3.
Putting that into our factors we get: |
|
*5 and 3 are two numbers whose
prod. is 15
*and sum is 8
|
Note that if we would multiply this out, we would get
the original
trinomial. |
|
Factoring Trinomials of the Form
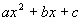
(where a does not
equal 1)
|
Again, this is the reverse of the FOIL method.
The difference between this trinomial and the one
discussed above, is
there is a number other than 1 in front of the x squared. This means, that not only do
you
need to find factors of c, but also a.
Step 1:
Set up a
product of two ( ) where each will hold two terms.
It will look like this
( )(
) |
Step 2: Use trial and
error to find the factors needed.
The factors of a will
go in the first
terms of the binomials and the factors of c will go in the last terms of the binomials.
The trick is to get the right combination of these
factors. You
can check this by applying the FOIL method. If your product comes
out to be the trinomial you started with, you have the right
combination
of factors. If the product does not come out to be the given
trinomial,
then you need to try again. |
|
Note that this trinomial does not have a GCF.
So we go right into factoring the trinomial of the
form 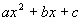 . . |
Step 1: Set up
a product of two ( ) where each will hold two terms. |
It will look like this:
(
)( ) |
Step 2: Use trial and
error to find the factors needed. |
In the first terms of the binomials, we need factors
of 3 x squared. This would have to be 3x and x.
In the second terms of the binomials, we need factors
of 2.
This would have to be 2 and 1. I used positives here because the
middle term is positive.
Also, we need to make sure that we get the right
combination of these
factors so that when we multiply them out we get 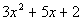 . . |
|
Possible Factor
|
Check using the FOIL Method
|
First try:
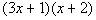
|
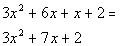
This is not our original polynomial.
So we need to try again.
|
|
Second try:
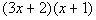
|
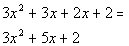
This is our original polynomial.
So this is the correct combination of factors for
this polynomial.
|
This process takes some
practice. After
a while you will get used to it and be able to come up with the right
factor
on the first try. |
Note that this trinomial does not have a GCF.
So we go right into factoring the trinomial of the
form 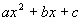 |
Step 1: Set up
a product of two ( ) where each will hold two terms. |
It will look like this:
(
)( ) |
Step 2: Use
trial and
error to find the factors needed. |
In the first terms of the binomials, we need factors
of 5 x squared.
This would have to be 5x and x.
In the second terms of the binomials, we need factors
of -8.
This would have to be -8 and 1, 8 and -1, 2 and -4, or -2 and 4.
Since the product of these factors has to be a negative number, we need
one positive factor and one negative factor.
Also we need to make sure that we get the right
combination of these
factors so that when we multiply them out we get 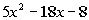 . . |
|
Possible Factors
|
Check using the FOIL Method
|
First try:
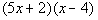
|
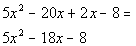
This is our original polynomial.
So this is the correct combination of factors for
this polynomial.
|
Not every polynomial is factorable. Just like not
every number
has a factor other than 1 or itself. A prime number is a number
that
has exactly two factors, 1 and itself. 2, 3, and 5 are examples
of
prime numbers.
The same thing can occur with polynomials. If
a polynomial
is not factorable we say that it is a prime polynomial.
Sometimes you will not know it is prime until you start
looking for
factors of it. Once you have exhausted all possibilities, then
you
can call it prime. Be careful. Do not think because you
could not factor it on the first try that it is prime. You must
go
through ALL possibilities first before declaring it prime. |
Note that this trinomial does not have a GCF.
So we go right into factoring the trinomial of the
form 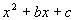 . . |
Step 1: Set up a product
of two ( ) where each will hold two terms. |
It will look like
this:
(
)( ) |
Step 2: Find
the factors
that go in the first positions. |
Since we have x squared
as our first term,
we will need the following:
(x
)(x ) |
Step 3:
Find the
factors that go in the last positions. |
We need two numbers whose product is 12 and sum is 5.
Can you think of any????
Since the product is a positive number and the sum is
a positive
number, we only need to consider pairs of numbers where both signs are
positive.
One pair of factors of 12 is 3 and 4, which does not
add up to be 5.
Another pair of factors are 2 and 6, which also does not
add up
to 5.
Another pair of factors are 1 and 12, which also does
not add up
to 5.
Since we have looked at ALL the possible factors, and
none of them
worked, we can say that this polynomial is prime.
In other words, it does not factor. |
|
Factoring
a Perfect Square
Trinomial
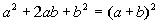
OR
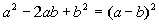
|
It has to be exactly in this form to use this
rule. When you
have a base being squared plus or minus twice the product of the two
bases
plus another base squared, it factors as the sum (or difference) of the
bases being squared.
This is the reverse
of the
binomial squared found in Tutorial 6: Polynomials. Recall
that factoring is the reverse of multiplication. |
First note that there is no GCF to factor out of this
polynomial.
Since it is a trinomial, you can try factoring this by trial and error shown above. But if you can recognize
that
it fits the form of a perfect square trinomial,
you can save yourself some time. |
|
*Fits the form of a perfect sq.
trinomial
*Factor as the sum of bases squared
|
Note that if we would multiply this out, we would get
the original
polynomial. |
First note that there is no GCF to factor out of this
polynomial.
Since it is a trinomial, you can try factoring this by trial and error shown above. But if you can recognize
that
it fits the form of a perfect square trinomial,
you can save yourself some time. |
|
*Fits the form of a perfect sq.
trinomial
*Factor as the diff. of bases
squared
|
Note that if we would multiply this out, we would get
the original
polynomial. |
|
Factoring
a Difference of
Two Squares
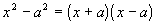
|
Note that the sum of two
squares DOES NOT
factor.
Just like the perfect square trinomial, the difference
of two squares
has to be exactly in this form to use this rule. When
you
have the difference of two bases being squared, it factors as the
product
of the sum and difference of the bases that are being squared.
This is the reverse
of the
product of the sum and difference of two terms found in Tutorial 6:
Polynomials.
Recall that factoring is the reverse of multiplication. |
First note that there is no GCF to factor out of this
polynomial.
This fits the form of a the difference
of two squares.
So we will factor using that rule: |
|
*Fits the form of a diff. of two
squares
*Factor as the prod. of sum and
diff. of bases
|
Note that if we would multiply this out, we would get
the original
polynomial. |
First note that there is no GCF to factor out of this
polynomial.
This fits the form of the difference
of two squares.
So we will factor using that rule: |
|
*Fits the form of a diff. of two
squares
*Factor as the prod. of sum and
diff. of bases
|
Note that if we would multiply this out and the
original expression
out we would get the same polynomial. |
|
Factoring
a Sum of Two Cubes
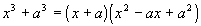
|
The sum of two cubes has to be exactly in this
form to use this
rule. When you have the sum of two cubes, you have a product
of
a binomial and a trinomial. The binomial is the sum of the bases
that are being cubed. The trinomial is the first base squared,
the
second term is the opposite of the product of the two bases found, and
the third term is the second base squared. |
First note that there is no GCF to factor out of this
polynomial.
This fits the form of the
sum of cubes.
So we will factor using that rule: |
|
*Fits the form of a sum of two
cubes
*Binomial is sum of bases
*Trinomial is 1st base squared,
minus prod.
of bases, plus 2nd base squared |
Note that if we would multiply this out, we would get
the original
polynomial. |
|
Factoring
a Difference of
Two Cubes
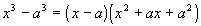
|
This is factored in a similar fashion to the sum of two
cubes.
Note the only difference is that the sign in the binomial is a - which
matches the original sign, and the sign in front of ax is positive,
which
is the opposite sign. The difference of two cubes has to be exactly in this
form to use this
rule. When you have the difference of two cubes, you have a
product
of a binomial and a trinomial. The binomial is the difference of
the bases that are being cubed. The trinomial is the first base
squared,
the second term is the opposite of the product of the two bases found,
and the third term is the second base squared. |
First note that there is no GCF to factor out of this
polynomial.
This fits the form of the
difference of
cubes. So we will factor using that rule: |
|
*Fits the form of a diff. of
two cubes
*Binomial is diff. of bases
*Trinomial is 1st base squared,
plus prod.
of bases, plus 2nd base squared |
Note that if we would multiply this out, we would get
the original
polynomial. |
Now that you have a list of different factoring rules,
let’s put it
all together. The following is a checklist of the factoring rules
that we have covered in our tutorials.
When you need to factor, you
ALWAYS look for
the GCF first. Whether you have a GCF or not, then
you continue looking to see if you have anything else that
factors.
Below is a checklist to make sure you do not miss
anything. Always
factor until you can not factor any further. |
|
Factoring Strategy
I. GCF:
Always check for the GCF first, no matter what. |
II. Binomials:
III. Trinomials:
a. 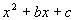
b. Trial and error:
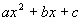
c. Perfect square trinomial:
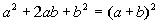
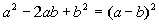
|
IV. Polynomials with four terms:
|
The first thing that we always check when we are
factoring is WHAT?
The GCF. In this case, there is one.
Factoring out the GCF of 3 we get: |
|
*Factor a 3 out of every term
|
Next, we assess to see if there is anything else that
we can factor.
We have a trinomial inside the ( ). It fits the form
of a perfect square trinomial, so we will
factor
it accordingly: |
|
*Fits the form of a perfect sq.
trinomial
*Factor as the sum of bases squared
|
There is no more factoring that we can do in this
problem.
Note that if we would multiply this out, we would get
the original polynomial. |
The first thing that we always check when we are
factoring is WHAT?
The GCF. In this case, there is not one.
So we assess what we have. It fits the form of a difference
of two squares, so we will factor it accordingly: |
|
*Fits the form of a diff. of two
squares
*Factor as the prod. of sum and
diff. of bases
|
Next we assess to see if there is anything else that we
can factor.
Note how the second binomial is another difference
of two squares. That means we have to continue factoring
this problem. |
|
*Fits the form of a diff. of two
squares
*Factor as the prod. of sum and
diff. of bases
|
There is no more factoring that we can do in this
problem.
Note that if we would multiply this out, we would get
the original polynomial. |
The first thing that we always check when we are
factoring is WHAT?
The GCF. In this case, there is not one.
So we assess what we have. It fits the form of a sum
of two cubes, so we will factor it accordingly: |
|
*Fits the form of a sum of two
cubes
*Binomial is sum of bases
*Trinomial is 1st base squared,
minus prod.
of bases, plus 2nd base squared
|
There is no more factoring that we can do in this
problem.
Note that if we would multiply this out, we would get
the original polynomial. |
The first thing that we always check when we are
factoring is WHAT?
The GCF. In this case, there is not one.
So we assess what we have. This is a trinomial that does
not fit the
form of a perfect square trinomial. Looks like we will have to
use trial
and error: |
|
*Factor by trial and error
|
There is no more factoring that we can do in this
problem.
Note that if we would multiply this out, we would get
the original polynomial. |
The first thing that we always check when we are
factoring is WHAT?
The GCF. In this case, there is not one.
So we assess what we have. This is a polynomial with
four terms.
Looks like we will have to try factoring it by
grouping: |
|
*Group in two's
*Factor out the GCF out of each
separate (
)
*Factor out the GCF of (x + 5b)
|
There is no more factoring that we can do in this
problem.
Note that if we would multiply this out, we would get
the original polynomial. |
 Practice Problems Practice Problems
These are practice problems to help bring you to the
next level.
It will allow you to check and see if you have an understanding of
these
types of problems. Math works just like
anything
else, if you want to get good at it, then you need to practice
it.
Even the best athletes and musicians had help along the way and lots of
practice, practice, practice, to get good at their sport or instrument.
In fact there is no such thing as too much practice. To get the most out of these, you should work the
problem out on
your own and then check your answer by clicking on the link for the
answer/discussion
for that problem. At the link you will find the answer
as well as any steps that went into finding that answer. |
 Practice
Problems 1a - 1f: Factor completely. Practice
Problems 1a - 1f: Factor completely.
 Need Extra Help on these Topics? Need Extra Help on these Topics?

Videos at this site were created and produced by Kim Seward and Virginia Williams Trice.
Last revised on Dec. 13, 2009 by Kim Seward.
All contents copyright (C) 2002 - 2010, WTAMU and Kim Seward. All rights reserved.
|
|


