College Algebra
Tutorial 39: Zeros of Polynomial Functions, Part II:
Upper and Lower Bounds, Intermediate Value Theorem, Fundamental Theorem of Algebra, and the Linear Factorization Theorem
 Learning Objectives
After completing this tutorial, you should be able to:
- Determine if a given number is an upper or lower bound for roots of a
polynomial
function.
- Use the Intermediate Value Theorem to approximate real zeros of
polynomial
functions.
- Know that if a non-real complex number is a root of a polynomial
function
that its conjugate is also a root.
- Know what the Fundamental Theorem of Algebra is.
- Use the Linear Factorization Theorem to find an nth degree polynomial
function
given its zeros.
|
Introduction
In this tutorial we will be looking at several aspects
dealing with
zeros of polynomial functions. If you need a review on how to
find
zeros, the Rational Zero Theorem or Descartes' Rule of Signs, feel
free
to go to Tutorial 38: Zeros of
Polynomial
Functions, Part I. On this page we dive a little deeper
into
the concept of zeros. One thing that we will look at is finding
the
upper and lower bounds for roots of a polynomial function. This
can
help us narrow down the possibilities of rational zeros. Another
concept on this page is the Intermediate Value Theorem. This can
help narrow down the possibilities of real zeros, especially those that
land between integer values. We will also work with non-real
complex
numbers. Did you know that if a non-real complex number is a zero
of a polynomial function, that its conjugate is too? We
will
follow that up by using the Fundamental Theorem of Algebra and the
Linear
Factorization Theorem to find polynomial functions given zeros.
Wow,
it looks like we have our work cut out for us. I guess you better
get started. |
Tutorial
|
The Upper and Lower Bound
Theorem
|
Upper Bound
If you divide a polynomial function f(x)
by (x - c),
where c > 0, using synthetic division and this yields all positive numbers,
then c is an upper bound to the real roots of the equation f(x)
= 0.
Note that two things must occur for c to
be an upper bound. One is c > 0
or positive.
The other is that all the coefficients of the quotient as well as the
remainder
are positive. |
Lower Bound
If you divide a polynomial function f(x)
by (x - c),
where c < 0, using synthetic division and this yields alternating signs,
then c is a lower bound to the real roots of the equation f(x)
= 0. Special note that zeros can be either positive or
negative.
Note that two things must occur for c to
be a lower bound. One is c < 0
or
negative. The other is that successive coefficients of the
quotient
and the remainder have alternating signs. |
 Example
1: Show that all real roots of the equation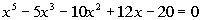 
lie between - 4 and 4. |
In other words, we need to show that - 4 is a lower
bound and 4 is
an upper bound for real roots of the given equation.
Checking the
Lower Bound:
Lets apply synthetic division with - 4 and see if we get alternating signs:
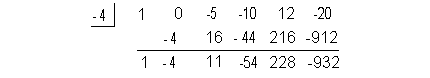
Note how c = -4 < 0 AND the successive
signs in the bottom row of our synthetic division alternate.
You know what that means?
- 4 is a lower bound for the real roots of this
equation. |
Checking the
Upper Bound:
Lets apply synthetic division with 4 and see if we get all positive:
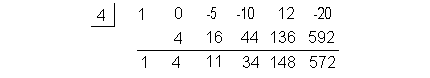
Note how c = 4 > 0 AND the all
of the signs in the bottom row of our synthetic division are
positive.
You know what that means?
4 is an upper bound for the real roots of this
equation.
Since - 4 is a lower bound and 4 is an upper bound for
the real roots
of the equation, then that means all real roots of the equation lie
between - 4 and 4. |
|
The Intermediate Value
Theorem
If f(x) is a
polynomial function and f(a)
and f(b) have different signs, then there is at least
one
value, c,
between a and b such that f(c)
= 0.
|
In other words, when you have a polynomial function and
one input value
causes the function to be positive and the other negative, then there
has
to be at least one value in between them that causes the polynomial
function
to be 0.
This works because 0 separates the positives from the
negatives.
So to go from positive to negative or vice a versa you would have to
hit
a point in between that goes through 0. |
Example
2: Show that 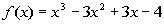 has a real zero between 2 and 3. Use the Intermediate Value
theorem
to find an approximation for this zero to the nearest tenth. |
When finding functional values, you can either use
synthetic division
or directly plug the number into the function. Since we will only
be interested in knowing the functional value in this problem, I’m
going
to directly plug my x value into the
function.
If I were needing more, for example the signs of the quotient, like
above,
then I would use synthetic division.
Finding f(2):
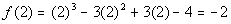
Finding f(3):
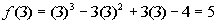
Since there is a sign change between f(2)
= -2 and f(3) = 5, then according to the Intermediate
Value Theorem, there is at least one value between 2 and 3 that
is a zero of this polynomial function.
Checking functional values at intervals of one-tenth
for a sign change: |
|
Finding f(2.1):
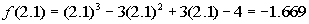
Finding f(2.2):
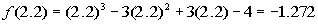
Finding f(2.3):
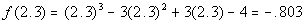
Finding f(2.4):
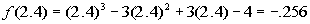
Finding f(2.5):
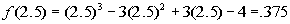
Hey we have a sign change!!!!!
Now we want to find the zero to the nearest tenth.
So is it going
to be x = 2.4 or x = 2.5. We can not necessarily go by which functional value is
closer
to zero.
We will need to dig a little bit deeper and go by
intervals of one-hundredths: |
|
Finding f(2.41):
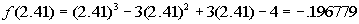
Finding f(2.42):
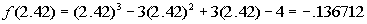
Finding f(2.43):
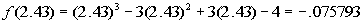
Finding f(2.44):
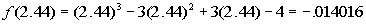
Finding f(2.45):
 |
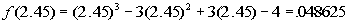Whew!!!! At last we come to a sign change between
successive
hundredths. That means we have it narrowed down at little bit
better.
There is a zero between 2.44 and 2.45.
Since it would land slightly below 2.45, the nearest
tenth would
be 2.4.
The work here is not hard, it is just tedious. |
|
Fundamental Theorem of
Algebra
Every polynomial function equation f(x)
= 0 of degree one or higher has at least one complex root.
|
Keep in mind that complex numbers include real
numbers. Real
numbers are complex numbers where the imaginary part is 0. |
In polynomial function equations, non-real complex roots
always occur
in conjugate pairs.
In other words, if a complex number with an imaginary
part is a root
of a polynomial function equation, then its conjugate is also a root of
that same function.
Remember that a conjugate of a + bi is a - bi.
So, if 2 + 3i is a known root of a
polynomial
function equation, then 2 - 3i is also.
If you need a review on complex numbers, feel free to go
to Tutorial
12: Complex Numbers. |
|
The Linear Factorization
Theorem
If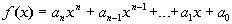 
where n > 1
and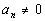 
then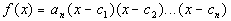 
where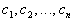 
are complex numbers
(possibly real and not necessarily
distinct)
|
In other words, a polynomial function of degree n,
where n > 0, can be factored
into n (not necessarily distinct) linear factors over the complex number
field.
Keep in mind that some factors may occur more than one
time. For
each time a linear factor appears it is counted as a linear
factor.
For example, if  ,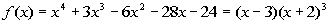
the linear factor (x + 2) has a
multiplicity
of 3, which means that factor occurs three times. So technically
there are 4 linear factors, one (x - 3)
and
three (x + 2)’s. This matches the
degree
of the polynomial function. |
Example
3: Use the given root to find all of the roots of the
polynomial
equation  ;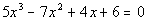
1 + i. |
Since the complex number 1 + i is a root,
that means it’s conjugate 1 - i is also a root. This will help us break down the function to find
any other roots. This is done in the same fashion as when you are given a
real zero.
If you need a review on finding roots of a polynomial
equation f(x)
= 0 when given a root, feel free to go to Tutorial
37: Synthetic Division and the Remainder and Factor Theorems.
Using synthetic division to find the quotient we
get:
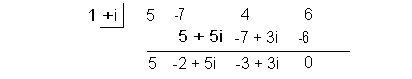
Yuck!!! Look at all of those complex numbers
in the quotient.
Don’t fear, when we put in our conjugate using that quotient those
complex
numbers will disappear and we will be left with a nice quotient with
real
number coefficients.
Check it out:
|
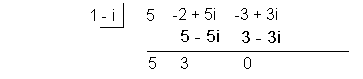
Now we are getting somewhere. From here we can
rewrite the original
problem using the roots that we have above and the quotient that we
ended
up with in this last synthetic division. |
|
*The 1st two factors are x minus the complex zeros
*The 3rd factor is the quotient
found directly
above
*The given complex zero
*The conjugate zero
*Setting the 3rd factor = 0
|
So the roots of the polynomial equation are 1 + i,
1 - i and -3/5. |
Example
4: Factor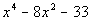 
a) as the product of factors that are irreducible over rational
numbers,
b) as the product of factors that are irreducible over real numbers,
and
c) in completely factored form involving complex non-real numbers. |
Factor as the product of factors that are
irreducible over rational
numbers: |
Since 11 is not a perfect square, this is as far as we
can factor it
using only rational numbers.
Factor as the product of factors that are irreducible
over real numbers: |
Did you know that the sum of squares can be factored
over the complex
non-real numbers as  ?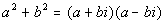
Completely factored form involving complex non-real
numbers:
|
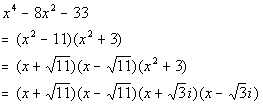
Note how once we had factored over the complex numbers
that we ended
up with four linear factors and that our polynomial was degree four. |
|
Creating a Polynomial
Function when Given
Zeros
|
Now we are going to reverse things. In the next
two examples,
we will be given zeros and the degree of a polynomial function, and we
will need to find out what that polynomial is.
Step 1: Use the given
zeros and the Linear Factorization Theorem to write out all of the
factors
of the polynomial function.
Keep in mind that if you are given a non-real
complex zero, that its
conjugate is also a zero.
Also keep in mind that the degree tells you how
many linear factors
over the complex numbers (possibly real and not necessarily distinct)
that
you will have.
The factors are written in the following way: if c is a zero than (x - c)
is a factor of the polynomial function. |
Step 2: Multiply all of
the factors found in Step 1. |
Example
5: Find an nth degree
polynomial
function where n = 3; 2 + 3 i and 4 are zeros; f(3) = -20. |
Since our degree is 3, that means there are three
linear factors over
the complex numbers (possibly real and not necessarily distinct).
Note how we are only given two zeros. We need to
come up with
a third one. Do you have any ideas?
Oh yeah, if a non-real complex number is a zero than its
conjugate is
also a zero. Since 2 + 3i is a
zero,
that means 2 - 3i is also a zero.
Using the Linear Factorization Theorem we
get:
|
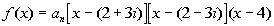
Step 2: Multiply all
of the factors found in Step 1. |
|
*Dist. - through comp. numbers
*Multiply comp. factors
*Simplify (i squared
= -1)
*Multiply remaining factors
|
This problem gave another condition, f(3)
= -20.
This will help us find in this problem. |
|
*f(3)
= -20
*Solve for a sub n
|
Putting it all together we get:
|
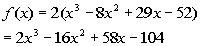
Practice Problems
These are practice problems to help bring you to the next level.
It will allow you to check and see if you have an understanding of these
types of problems. Math works just like anything
else, if you want to get good at it, then you need to practice it.
Even the best athletes and musicians had help along the way and lots of
practice, practice, practice, to get good at their sport or instrument.
In fact there is no such thing as too much practice. To get the most out of these, you should work the problem out on
your own and then check your answer by clicking on the link for the answer/discussion
for that problem. At the link you will find the answer
as well as any steps that went into finding that answer. |
 Practice
Problem 1a: Show that all real roots of the
given equation
lie between -3 and 4.
Practice
Problem 2a: Show that the given polynomial has a
real zero between
the given integers. Use the Intermediate Value theorem to find an
approximation for this zero to the nearest tenth.
Practice
Problem 3a: Use the given root to find all of the
roots of the
given polynomial equation.
Practice
Problem 4a: Factor the given polynomial
function a) as the
product of factors that are irreducible over rational numbers, b) as
the
product of factors that are irreducible over real numbers, and c) in
completely
factored form involving complex non-real numbers.
Practice
Problem 5a: Find an nth degree polynomial
function with
the given conditions
Need Extra Help on these Topics?
Last revised on March 15, 2012 by Kim Seward.
All contents copyright (C) 2002 - 2012, WTAMU and Kim Seward. All rights reserved.
|
|
;
between -1 and -2. 
;
2i 