College Algebra
Answer/Discussion to Practice Problems
Tutorial 39: Zeros of Polynomial Functions, Part II:
Upper and Lower Bounds, Intermediate Value Theorem, Fundamental Theorem of Algebra,
and the Linear Factorization Theorem
 Answer/Discussion
to 1a
|
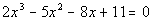
In other words, we need to show that -3 is a lower bound and 4 is an
upper bound for real roots of the given equation.
Checking the Lower Bound:
Lets apply synthetic division with -3 and see if we get alternating signs:
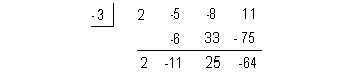
Note how c = -3 < 0 AND the successive
signs in the bottom row of our synthetic division alternate.
You know what that means?
-3 is a lower bound for the real roots of this equation. |
Checking the Upper Bound:
Lets apply synthetic division with 4 and see if we get all positive:
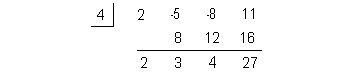
Note how c = 4 > 0 AND the all
of the signs in the bottom row of our synthetic division are positive.
You know what that means?
4 is an upper bound for the real roots of this equation.
Since -3 is a lower bound and 4 is an upper bound for the real roots
of the equation, then that means all real roots of the equation lie
between -3 and 4. |
Answer/Discussion
to 2a
|
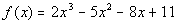
When finding functional values, you can either use synthetic division
or directly plug the number into the function. Since we will only
be interested in knowing the functional value in this problem, I'm going
to directly plug my x value into the function.
If I were needing more, for example the signs of the quotient, like above,
then I would use synthetic division.
Finding f(-2):
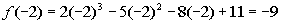
Finding f(-1):
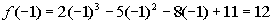
Since there is a sign change between f(-2)
= -9 and f(-1) = 12, then according to the Intermediate
Value Theorem, there is at least one value between -2 and -1 that
is a zero of this polynomial function.
Checking functional values at intervals of one-tenth for a sign change: |
|
Finding f(-1.1):
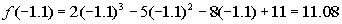
Finding f(-1.2):
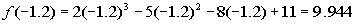
Finding f(-1.3):
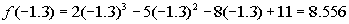
Finding f(-1.4):
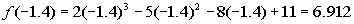
Finding f(-1.5):
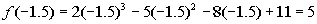
Finding f(-1.6):
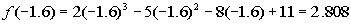
Finding f(-1.7):
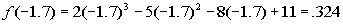
Finding f(-1.8):
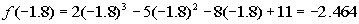
Hey we have a sign change!!!!!
Now we want to find the zero to the nearest tenth. So is it going
to be x = -1.7 or x = -1.8. We can not necessarily go by which functional value is closer
to zero.
We will need to dig a little bit deeper and go by intervals of one-hundredths: |
|
Finding f(-1.71):
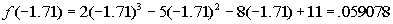
Finding f(-1.72):
 |
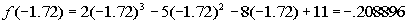Whew!!!! At last we come to a sign change between successive
hundredths. That means we have it narrowed down at little bit better.
There is a zero between -1.71 and -1.72.
Since it would land slightly below -1.71, the nearest tenth would
be -1.7.
The work here is not hard, it is just tedious. |
Answer/Discussion
to 3a
|
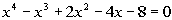
Since the complex number 2 i is a root,
that means it's conjugate -2 i is also a root. This will help us
break down the function to find any other roots. This is done in the same fashion as when you are given a real zero.
If you need a review on finding roots of a polynomial equation f(x)
= 0 when given a root, feel free to go to Tutorial
37: Synthetic Division and the Remainder and Factor Theorems.
Using synthetic division to find the quotient we get:
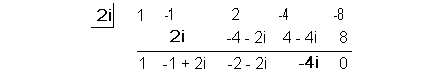
Yuck!!! Look at all of those complex numbers in the quotient.
Don't fear, when we put in our conjugate using that quotient those complex
numbers will disappear and we will be left with a nice quotient with real
number coefficients.
Check it out:
|
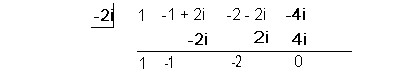
Now we are getting somewhere. From here we can rewrite the original
problem using the roots that we have above and the quotient that we ended
up with in this last synthetic division. |
|
*The 1st two factors are x minus the complex zeros
*The 3rd factor is the quotient found directly
above
*Factor the trinomial
*The given complex zero
*The conjugate zero
*Setting the 3rd factor = 0
*Setting the 4th factor = 0
|
So the roots of the polynomial equation are 2i,
-2i, 2, and -1. |
Answer/Discussion
to 4a
|
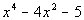
Factor as the product of factors that are irreducible over rational
numbers: |
Since 5 is not a perfect square, this is as far as we can factor it
using only rational numbers.
Factor as the product of factors that are irreducible over real numbers: |
Did you know that the sum of squares can be factored over the complex
non-real numbers as  ?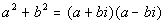
Completely factored form involving complex non-real numbers:
|
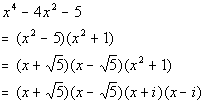
Note how once we had factored over the complex numbers that we ended
up with four linear factors and that our polynomial was degree four. |
Answer/Discussion
to 5a
n = 4; 2, -1, and 2i are zeros; f(1) = -30. |
Since our degree is 4, that means there are four linear factors over
the complex numbers (possibly real and not necessarily distinct).
Note how we are only given two zeros. We need to come up with
a third one. Do you have any ideas?
Oh yeah, if a non-real complex number is a zero than its conjugate is
also a zero. Since 2i is a zero, that
means -2i is also a zero.
Using the Linear Factorization
Theorem we get:
|
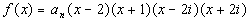
Step 2: Multiply all
of the factors found in Step 1. |
|
*Multiply comp. factors
*Multiply remaining factors
|
This problem gave another condition, f(1)
= -30.
This will help us find in this problem. |
|
*f(1) = -30
*Solve for a sub n
|
Putting it all together we get:
|
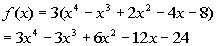
Last revised on March 15, 2010 by Kim Seward.
All contents copyright (C) 2002 - 2012, WTAMU and Kim Seward. All rights reserved.
|
|
