College Algebra
Tutorial 37: Synthetic Division and
the Remainder and Factor Theorems
 Learning Objectives Learning Objectives
After completing this tutorial, you should be able to:
- To divide a polynomial by a binomial of the form x - c using synthetic division.
- Use the Remainder Theorem in conjunction with synthetic division to find
a functional value.
- Use the Factor Theorem in conjunction with synthetic division to find factors
and zeros of a polynomial function.
|
 Introduction Introduction
In this tutorial we are going to look at synthetic division.
You can use synthetic division whenever you need to divide a polynomial
function by a binomial of the form x - c.
We can use this to find several things. One is the actual quotient
and remainder you get when you divide the polynomial function by x - c. Also, the Remainder Theorem states that
the remainder that we end up with when synthetic division is applied actually
gives us the functional value. Another use is finding factors and
zeros. The Factor Theorem states that if the functional value is
0 at some value c, then x - c is a factor and c is a zero. You can not only find that functional value by using synthetic
division, but also the quotient found can help with the factoring process.
Sounds like synthetic division can help us out on several different types
of problems. I think you are ready to go discover the
wonderful world of synthetic division. |
 Tutorial Tutorial
Synthetic division is another way to divide a polynomial by the binomial x - c , where c is
a constant. |
Step 1: Set up the synthetic
division. |
An easy way to do this is to first set it up as if you are doing long
division and then set up your synthetic division.
If you need a review on setting up a long division problem, feel free
to go to Tutorial 36: Long
Division.
The divisor (what you are dividing by) goes on the outside of the box.
The dividend (what you are dividing into) goes on the inside of the box.
When you write out the dividend make sure that you write it in descending
powers and you insert 0's for any missing terms. For example, if
you had the problem 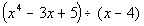 ,
the polynomial ,
the polynomial 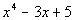 ,
starts out with degree 4, then the next highest degree is 1. It is missing
degrees 3 and 2. So if we were to put it inside a division box we
would write it like this: ,
starts out with degree 4, then the next highest degree is 1. It is missing
degrees 3 and 2. So if we were to put it inside a division box we
would write it like this:
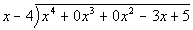 . .
This will allow you to line up like terms when you go through the problem.
When you set this up using synthetic division write c for the divisor x - c.
Then write the coefficients of the dividend to the right, across the top.
Include any 0's that were inserted in for missing terms.

|
Step 2: Bring down
the leading coefficient to the bottom row. |
Step 3: Multiply c by the value just written on the bottom row. |
Place this value right beneath the next coefficient in the dividend:
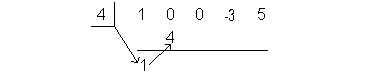
|
Step 4: Add the
column created in step 3. |
Write the sum in the bottom row:
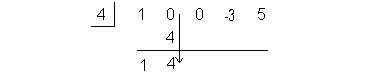
|
Step 5: Repeat
until done. |
Step 6: Write out the
answer. |
The numbers in the last row make up your coefficients of the quotient
as well as the remainder. The final value on the right is the remainder.
Working right to left, the next number is your constant, the next is the
coefficient for x, the next is the coefficient
for x squared, etc...
The degree of the quotient is one less than the degree of the dividend.
For example, if the degree of the dividend is 4, then the degree of the
quotient is 3.
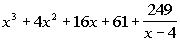
|
 Example
1 Example
1: Divide using synthetic division: 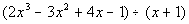 . |
Synthetic division would look like this:

|
|
*(-1)(2) = -2
*Place -2 in next column
|
The numbers in the last row make up your coefficients of the quotient
as well as the remainder. The final value on the right is the remainder.
Working right to left, the next number is your constant, the next is the
coefficient for x, the next is the coefficient
for x squared, etc...
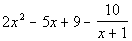
|
 Example
2 Example
2: Divide using synthetic division: 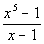 |
Synthetic division would look like this:

|
|
*(1)(1) =1
*Place 1 in next column
|
The numbers in the last row make up your coefficients of the quotient
as well as the remainder. The final value on the right is the remainder.
Working right to left, the next number is your constant, the next is the
coefficient for x, the next is the coefficient
for x squared, etc...
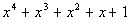
|
|
Remainder Theorem
If the polynomial f(x)
is divided by x - c, then
the reminder is f(c).
|
This means that we can apply synthetic division and the last number
on the right, which is the remainder, will tell us what the functional
value of c is. |
 Example
3 Example
3: Given 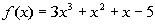 ,
use the Remainder Theorem to find f(-2). |
|
Using synthetic division to find the remainder we get:
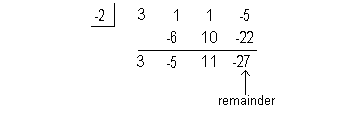
Again, our answer this time is not a quotient, but the remainder.
Final answer: f(-2) = -27 |
|
Factor Theorem
If f(x) is a polynomial AND
1) f(c) = 0, then x - c is a factor of f(x).
2) x - c is a factor of f(x),
then f(c) = 0.
|
Keep in mind that the division algorithm is
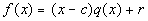
dividend = divisor(quotient)+ reminder
So if the reminder is zero, you can use this to help you factor a polynomial.
If x - c is a factor,
you can rewrite the original polynomial as (x - c) (quotient).
You can use synthetic division to help you with this type of problem.
The Remainder Theorem states that f(c)
= the remainder. So if the remainder comes out to be 0 when you apply
synthetic division, then x - c is a factor of f(x). |
 Example
4 Example
4: Use synthetic division to divide 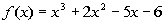 by x - 2. Use the result to find
all zeros of f. |
|
Using synthetic division to find the quotient we get:
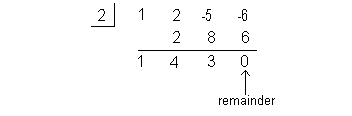
Note how the remainder is 0. This means that (x - 2) is a factor of 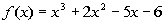 . . |
Rewriting f(x)
as (x - 2)(quotient) we get:
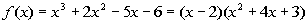
We need to finish this problem by setting this equal to zero and
solving it: |
|
*Set 1st factor = 0
*Set 2nd factor = 0
*Set 3rd factor = 0
|
The zeros of this function are x = 2,
-3, and -1. |
 Example
5 Example
5: Solve the equation 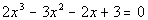
given that 3/2 is a zero (or root) of 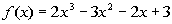 . |
|
Using synthetic division to find the quotient we get:
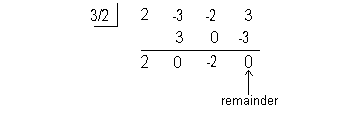
Note how the remainder is 0. This means that (x - 3/2) is a factor of 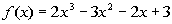 . . |
Rewriting f(x)
as (x - 3/2)(quotient) we get:
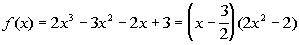
We need to finish this problem by setting this equal to zero and
solving it: |
|
*Factor the difference
of squares
*Note the 1st factor is 2, which is a constant,
which can never = 0
*Set 2nd factor = 0
*Set 3rd factor = 0
*Set 4th factor = 0
|
The solution or zeros of this function are x = 3/2, -1, and 1. |
 Practice Problems Practice Problems
These are practice problems to help bring you to the next level.
It will allow you to check and see if you have an understanding of these
types of problems. Math works just like anything
else, if you want to get good at it, then you need to practice it.
Even the best athletes and musicians had help along the way and lots of
practice, practice, practice, to get good at their sport or instrument.
In fact there is no such thing as too much practice. To get the most out of these, you should work the problem out on
your own and then check your answer by clicking on the link for the answer/discussion
for that problem. At the link you will find the answer
as well as any steps that went into finding that answer. |
 Practice
Problem 1a: Divide using synthetic division. Practice
Problem 1a: Divide using synthetic division.
 Practice
Problem 2a: Given the function f(x), use the Remainder
Theorem to find f(-1). Practice
Problem 2a: Given the function f(x), use the Remainder
Theorem to find f(-1).
 Practice
Problem 3a: Solve the given equation given that 1/2 is a zero (or
root) of Practice
Problem 3a: Solve the given equation given that 1/2 is a zero (or
root) of 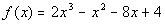 . .
 Need Extra Help on these Topics? Need Extra Help on these Topics?
The following are webpages that can assist
you in the topics that were covered on this page:
|

Last revised on March 15, 2012 by Kim Seward.
All contents copyright (C) 2002 - 2012, WTAMU and Kim Seward. All rights reserved.
|
|


