Answer/Discussion on Synthetic Division

(Back to the tutorial on synthetic division)

College Algebra
Answer/Discussion to Practice Problems
on Synthetic Division and
the Remainder and Factor Theorems

Answer/Discussion to 1a

Step 1: Set up the synthetic division.

Long division would look like this:

Synthetic division would look like this:

Step 2: Bring down the leading coefficient to the bottom row.

*Bring down the 4

Step 3: Multiply c by the value just written on the bottom row.

*(-1)(4) = -4
*Place -4 in next column

Step 4: Add the column created in step 3.

*0 + (-4) = -4

Step 5: Repeat until done.

Step 6: Write out the answer.

The numbers in the last row make up your coefficients of the quotient as well as the remainder. The final value on the right is the remainder. Working right to left, the next number is your constant, the next is the coefficient for x, the next is the coefficient for x squared, etc...

(return to problem 1a)

Answer/Discussion to 2a

The steps to the synthetic division are the same as described above. What is different is what are final answer is going to be. This time, we are looking for the functional value, so our answer will not be a quotient, but only the reminder.

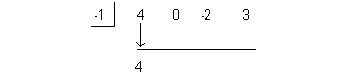
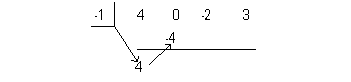
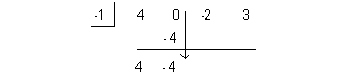
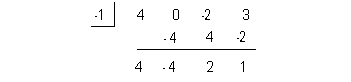
Using synthetic division to find the remainder we get:

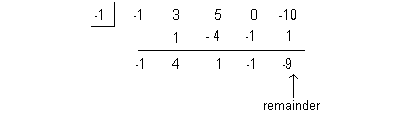
Again, our answer this time is not a quotient, but the remainder.

Final answer: f(-1) = -9

(return to problem 2a)

Answer/Discussion to 3a

The steps to the synthetic division are the same as described above. What is different is what are final answer is going to be. This time, we are looking for all of the zeros of f. We will start by dividing using synthetic division and then rewrite f(x) as (x - 1/2)(quotient).

Using synthetic division to find the quotient we get:

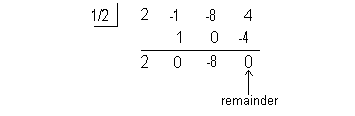
Note how the remainder is 0. This means that (x - 1/2) is a factor of .

Rewriting f(x) as (x - 1/2)(quotient) we get:

We need to finish this problem by setting this equal to zero and solving it:

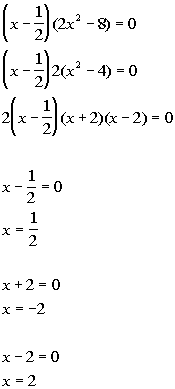
*Factor the difference of squares

*Set 1st factor = 0

*Set 2nd factor = 0

*Set 3rd factor = 0

The solution or zeros of this function are x = 1/2, -2, and 2.

(return to problem 3a)

(Back to the tutorial on synthetic division)