College Algebra
Tutorial 41: Practice Test on Tutorials 34 - 40
 Learning Objectives Learning Objectives
After completing this tutorial, you should be able to:
- Take a test on topics covered in tutorials 34 - 40 in this website.
|
Special Notes about Tutorial 41:
-
I can not guarantee
you will pass
your test after going though any of the tutorials in this website or
this
practice test. However, it will definitely help you to better
understand
the topics covered better.
-
Disclaimer: WTAMU and Kim Seward are not
responsible
for how a student does on any test or any class for any reason
including
not being able to access the website due to any technology
problems.
-
There are no videos on this page.
|
 Introduction Introduction
It
is important to note that, chances, are I'm not your math instructor. You need to check with your math teacher as to things like when your
next math test is and what it covers. It may cover more material
on the test than what is in this practice test. Just note that
there are other practice tests at this website. So, after finding out what
is on your test (if you have one) do the practice test(s) problems that
go with the test you are preparing for. If you are not in a class
or are not having a test soon, this practice test is still good practice
to go through and check to make sure you are understanding this material
before moving on - kind of like a spot check. The material on
this
practice test goes with Tutorial
34: Graphs of Quadratic Functions, Tutorial
35: Graphs of Polynomial Functions, Tutorial
36: Long Division, Tutorial
37: Synthetic Division and the Remainder and Factor Theorems, Tutorial
38: Zeros of Polynomial Functions, Part I, Tutorial
39: Zeros of Polynomial Functions, Part II, and Tutorial
40: Graphs of Rational Functions. Also note that your teacher may word the problems on their test a
little differently, may have some different kinds of problems, or may have
a different number of problems than what is in this practice test.
Again, since I'm probably not your math instructor, I don't know exactly
how your teacher will set up your math test. Just note that these
problems will help you build an understanding of the concepts presented
and the terms used in math problems. If you have an understanding
of the problems instead of just memorizing them, then you should do fine
on these concepts, no matter how the test is set up.
|
Steps to Studying for a Math Test
|
-
Work through problems. If you are in a class, you should have
done this on completion of any homework you have done. For anyone,
you can accomplish this by doing the practice problems found in each tutorial.
-
Check work on problems. The practice problems in each tutorial
have links to the answers to them so you can instantly check how you are
doing. Also, in most math books, the odd answers are found in the
back of the book.
-
Review concepts. Whether you got the problems right or wrong,
make sure you review over them. If you did get a problem wrong, make
sure you either review that concept in it's respective tutorial or ask
your math teacher about it. If you don't ask about a problem before
a test, you are going to kick yourself when it comes up on the test.
-
Work through problems as if you were taking the test - no notes, book,
webpages, etc. This practice test is a perfect way to do that. After
taking this practice test, check your answers by clicking on the link to
the answer key found at the bottom of the practice test (before the 'need
extra help on these topics' section)
|
|
It is to your benefit to show as much of the work as
possible on
the problems that have several steps involved.
Make sure that you read the directions carefully,
you wouldn't
believe how many points get taken off math tests for people not
following
directions.
Pace yourself. You do not have to be the
first one done
to do well on the test. Do not panic if there is still time left
to take the test and others are turing it in. Sometimes that
means
they do not know the material and left some of the answers blank.
Do not worry about anyone else but yourself.
Don't rush through a problem.
Another thing that
math teachers take points off for are careless mistakes made by people
that rush through a problem. When those students get their tests
back, they bonk themselves on the head at some of the things that got
counted
wrong, things that they knew how to do.
Check your answers. If you have time, go
back and check
your answers.
Remember to breathe!!!! I know some of you
are scared to
death at the thought of having to take a math test of any kind.
For
you guys, try to relax and don't forget to breathe. (Even if you
aren't scared to take a math test, it is probably a good idea to
remember to breathe, I wouldn't want you to pass out during the
test). If it feels like your brain has left the building during
your test,
just close your eyes and breathe in and out and in and out and your
brain
will return.
Good luck on your test. If you are taking a
math test soon,
don't panic, you are going to do great!!! |
 Practice Test Practice Test
Problems 1a - 1b: Find the coordinates of the
vertex of the
given quadratic function. Without graphing, determine if the
vertex
is the maximum or minimum point of the quadratic function. |
1a. 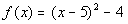 |
1b. 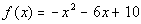 |
Problems 2a - 2b: Use the vertex and the
intercepts to sketch
the graph of the given quadratic function. Find the equation for
this function’s axis of symmetry. |
2a. 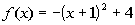 |
2b. 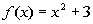 |
Problem 3a: Given the polynomial function a)
use the Leading
Coefficient Test to determine the graph’s end behavior, b) find the
x-intercepts
(or zeros) and state whether the graph crosses the x-axis or touches
the
x-axis and turns around at each x-intercept, c) find the y-intercept,
d)
determine the symmetry of the graph, e) indicate the maximum possible
turning
points, and f) graph. |
3a. 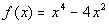 |
Problem 4a: Divide using long division. |
4a. 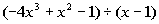 |
Problem 5a: Divide using synthetic division. |
5a. 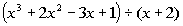 |
Problem 6a: Given the function f(x),
use the Remainder Theorem to find f(-2). |
6a. 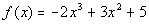 |
Problem 7a: Solve the given equation given
that 2/3 is a zero
(or root) of 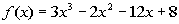 . . |
7a. 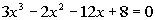 |
Problems 8a - 8b: List all of the possible
zeros or roots,
use Descartes’s Rule of Signs to possible narrow it down, use synthetic
division to test the possible zeros or roots and find an actual zero or
root, and use the actual zero to find all zeros or the actual root to
find
all solutions to the given polynomial function or equation to solve. |
8a. 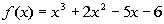 |
8b. 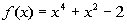 |
Problem 9a: Show that all real roots of the
given equation
lie between -2 and 2. |
9a. 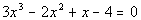 |
Problem 10a: Show that the given polynomial
has a real zero
between the given integers. Use the Intermediate Value theorem to
find an approximation for this zero to the nearest tenth. |
10a. 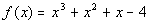 ;
between 1 and 2. |
Problem 11a: Use the given root to find all of
the roots of
the given polynomial equation. |
11a. 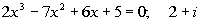 |
Problem 12a: Factor the given polynomial
function a)
as the product of factors that are irreducible over rational numbers,
b)
as the product of factors that are irreducible over real numbers, and
c)
in completely factored form involving complex nonreal numbers. |
12a. 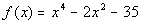 |
Problem 13a: Find an nth
degree
polynomial function with the given conditions. |
13a. n = 3; -3i and 2 are zeros and f(1) = -20 |
Problem 14a: Sketch the graph of the rational
function. |
14a. 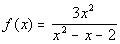
|
 Need Extra Help on these Topics? Need Extra Help on these Topics?

Last revised on March 20, 2011 by Kim Seward.
All contents copyright (C) 2002 - 2011, WTAMU and Kim Seward.
All rights reserved.
|
|


