College Algebra
Tutorial 36: Long Division

WTAMU > Virtual Math Lab > College Algebra

Learning Objectives

After completing this tutorial, you should be able to:

Divide one polynomial by another using long division.

Introduction

In this tutorial we revisit something that you may not have seen since grade school: long division. In this tutorial we are dividing polynomials, but it follows the same steps and thought process as when you apply it numbers. Let's forge ahead.

Tutorial

Divide

Polynomial Polynomial

Using Long Division

Step 1: Set up the long division.

The divisor (what you are dividing by) goes on the outside of the box. The dividend (what you are dividing into) goes on the inside of the box.

When you write out the dividend, make sure that you insert 0's for any missing terms. For example, if you had the polynomial 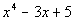, the first term has degree 4, then the next highest degree is 1. It is missing degrees 3 and 2. So if we were to put it inside a division box, we would write it like this:

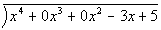
This will allow you to line up like terms when you go through the problem.

Step 2: Divide 1st term of dividend by first term of divisor to get first term of the quotient.

The quotient (answer) is written above the division box.

Make sure that you line up the first term of the quotient with the term of the dividend that has the same degree.

Step 3: Take the term found in step 2 and multiply it times the divisor.

Make sure that you line up all terms of this step with the term of the dividend that has the same degree.

Step 4: Subtract this from the line above.

Make sure that you subtract EVERY term found in step 3, not just the first one.

Step 5: Repeat until done.

You keep going until the degree of the "new" dividend is less than the degree of the divisor.

Step 6: Write out the answer.

Your answer is the quotient that you ended up with on the top of the division box.

If you have a remainder, write it over the divisor in your final answer.

Example 1: Divide using long division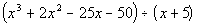

Step 1: Set up the long division.

*Write in descending order

Step 2: Divide 1st term of dividend by first term of divisor to get first term of the quotient.

Note that the "scratch work" that you see at the right of the long division shows you how that step is filled in. It shows you the "behind the scenes" of how each part comes about.

Scratch work:

Step 3: Take the term found in step 2 and multiply it times the divisor.

Scratch work:

Step 4: Subtract this from the line above.

Scratch work:

Step 5: Repeat until done.

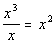
We keep going until we can not divide anymore. It looks like we can go at least one more time on this problem.

We just follow the the same steps 2 - 4 as shown above. Our "new dividend" is the last line .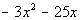

Step 2 (repeated): Divide 1st term of dividend by first term of divisor to get next term of the quotient.

Scratch work:

Step 3 (repeated): Take the term found in step 2 and multiply it times the divisor.

Scratch work:

Step 4 (repeated): Subtract this from the line above.

Scratch work:

Step 5: Repeat until done.

We keep going until we can not divide anymore. It looks like we can go one more time on this problem.

We just follow the the same steps 2 - 4 as shown above. Our "new dividend" is the last line .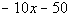

Step 2 (repeated): Divide 1st term of dividend by first term of divisor to get next term of the quotient.

Scratch work:

Step 3 (repeated): Take the term found in step 2 and multiply it times the divisor.

Scratch work:

Step 4 (repeated): Subtract this from the line above.

Scratch work:

Step 6: Write out the answer.

*Quotient with no remainder

Example 2: Divide using long division

Step 1: Set up the long division.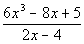

*Write in descending order
*Insert 0 for missing term

Step 2: Divide 1st term of dividend by first term of divisor to get first term of the quotient.

Note that the "scratch work" that you see at the right of the long division shows you how that step is filled in. It shows you the "behind the scenes" of how each part comes about.

Scratch work:

Step 3: Take the term found in step 2 and multiply it times the divisor.

Scratch work:

Step 4: Subtract this from the line above.

Scratch work:

Step 5: Repeat until done.

We keep going until we can not divide anymore.

We just follow the the same steps 2 - 4 as shown above. Our "new dividend" is always going to be the last line that was found in step 4.

Step 2 (repeated): Divide 1st term of dividend by first term of divisor to get next term of the quotient.

AND

Step 3 (repeated): Take the term found in step 2 and multiply it times the divisor.

AND

Step 4 (repeated): Subtract this from the line above.

The following is the scratch work (or behind the scenes if you will) for the rest of the problem. You can see everything put together following the scratch work under "putting it all together". This is just to show you how the different pieces came about in the final answer. When you work a problem like this, you don't necessarily have to write it out like this. You can have it look like the final product shown after this scratch work.

Scratch work for steps 2, 3 and 4
for the last two terms of the quotient

2nd term:

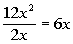
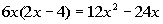
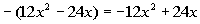
3rd term:

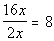
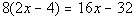
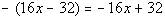
Putting it all together:

Note that each second line is SUBTRACTED, so the line shows what the signs of each term would be when you subtract it.

Step 6: Write out the answer.

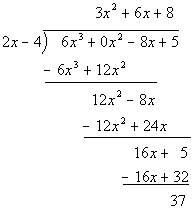
*Quotient with a remainder of 37

Practice Problems

These are practice problems to help bring you to the next level. It will allow you to check and see if you have an understanding of these types of problems. Math works just like anything else, if you want to get good at it, then you need to practice it. Even the best athletes and musicians had help along the way and lots of practice, practice, practice, to get good at their sport or instrument. In fact there is no such thing as too much practice.

To get the most out of these, you should work the problem out on your own and then check your answer by clicking on the link for the answer/discussion for that problem. At the link you will find the answer as well as any steps that went into finding that answer.

Practice Problems 1a - 1b: Divide using long division.

1a.

(answer/discussion to 1a)

1b.

(answer/discussion to 1b)

Need Extra Help on these Topics?

The following are webpages that can assist you in the topics that were covered on this page:

http://www.wtamu.edu/academic/anns/mps/math/mathlab/int_algebra/int_alg_tut35_div.htm
This webpage goes over long division.

http://www.purplemath.com/modules/polydiv.htm
This webpage goes over long division.

http://www.sosmath.com/algebra/factor/fac01/fac01.html
This webpage goes over long division.

Go to Get Help Outside the Classroom found in Tutorial 1: How to Succeed in a Math Class for some more suggestions.

WTAMU > Virtual Math Lab > College Algebra