College Algebra
Tutorial 35: Graphs of Polynomial Functions
 Learning Objectives Learning Objectives
After completing this tutorial, you should be able to:
- Identify a polynomial function.
- Use the Leading Coefficient Test to find the end behavior of the graph
of a given polynomial function.
- Find the zeros of a polynomial function.
- Find the multiplicity of a zero and know if the graph crosses the
x-axis
at the zero or touches the x-axis and turns around at the zero.
- Know the maximum number of turning points a graph of a polynomial
function
could have.
- Graph a polynomial function.
|
 Introduction Introduction
In this tutorial we will be looking at graphs of
polynomial functions.
If you need a review on functions, feel free to go to Tutorial
30: Introduction to Functions. If you need a review on
polynomials
in general, feel free to go to Tutorial
6: Polynomials. Basically, the graph of a polynomial
function
is a smooth continuous curve. There are several main aspects of
this
type of graph that you can use to help put the curve together. I
will be going over how to use the leading term of your polynomial
function
to determine the end behavior of its graph. We will also be
looking
at finding the zeros, aka the x-intercepts,
as well as the y-intercept of the graph.
If
you need a review on intercepts, feel free to go to Tutorial
26: Equations of Lines. Another important concept is to
know
the largest possible number of turning points. This will
help
you be more accurate in the graph that you draw. That just about
covers it. I guess you are ready to get to it. |
 Tutorial Tutorial
|
Polynomial Function
A polynomial function is a function
that can be written
in the form
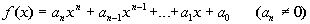 ,
where ,
where
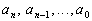 are real numbers and are real numbers and
n is a nonnegative integer.
|
|
Leading Term
When the polynomial function is
written in standard
form,
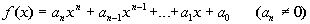 , ,
the leading term is 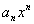 . .
|
In other words, the leading term is the term that the
variable has
its highest exponent.
The leading term of the function 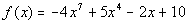 would be
would be 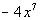 . .
|
|
Leading Coefficient
When the polynomial function is
written in standard
form,
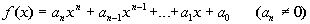 , ,
the leading coefficient is 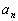 . .
|
Basically, the leading coefficient is the coefficient
on the leading
term.
The leading coefficient of the function 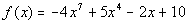 would be - 4.
would be - 4. |
|
Degree of a Term of a Polynomial
Function
|
The degree of a term of a polynomial function is the
exponent on the
variable. |
|
Degree of a Polynomial Function
When the polynomial function is
written in standard
form,
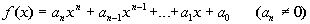 , ,
the degree of the polynomial function
is n.
|
The degree of the polynomial is the largest degree of
all of its terms.
The degree of the function 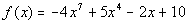 would be 7. would be 7. |
|
The Leading Coefficient Test
|
There are four cases that go with this test: |
Given a polynomial function in standard form 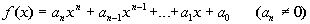 :
Case 1:
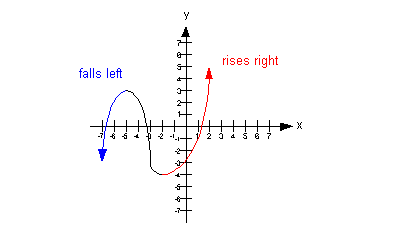
If n is odd AND the leading coefficient 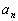 ,
is positive, the graph falls to the left and rises to
the
right: ,
is positive, the graph falls to the left and rises to
the
right:
|
Case 2:
If n is odd AND the leading coefficient 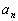 ,
is negative, the graph rises to the left and falls to
the
right. ,
is negative, the graph rises to the left and falls to
the
right.
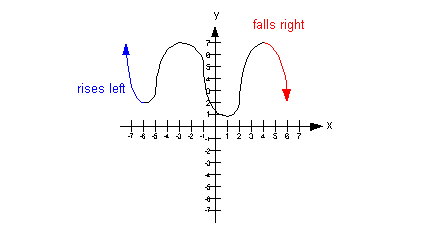
|
Case 3:
If n is even AND the leading coefficient 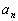 ,
is positive, the graph rises to the left and to the
right. ,
is positive, the graph rises to the left and to the
right.
|
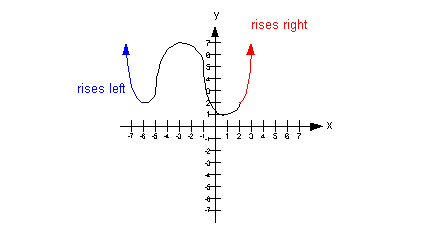
Case 4:
If n is even AND the leading coefficient 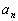 ,
is negative, the graph falls to the left and to the
right. ,
is negative, the graph falls to the left and to the
right.
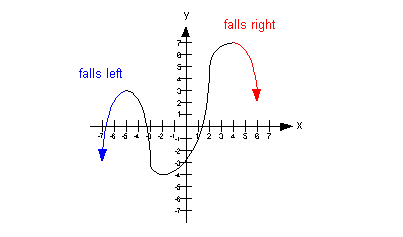
|
|
First question is what is the
leading term?
If you said 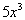 ,
you are correct!! ,
you are correct!!
Second question is what is the leading term’s degree?
If you said 3, you are right on!! 3 is the
exponent on the leading
term, which also means it is the degree of the polynomial.
Third question is what is the coefficient on the
leading term?
If you said 5, pat yourself on the back!!
Putting this information together with the Leading
Coefficient Test
we can determine the end behavior of the graph of our given polynomial:
Since the degree of the polynomial, 3, is odd and the
leading coefficient,
5, is positive, then the graph of the given polynomial falls to the
left and rises to the right. |
First question is what is the
leading term?
If you said 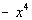 ,
you are correct!! ,
you are correct!!
Second question is what is the leading term’s degree?
If you said 4, you are right on!! 4 is the
exponent on the leading
term, which also means it is the degree of the polynomial.
Third question is what is the coefficient on the
leading term?
If you said -1, pat yourself on the back!!
Putting this information together with the Leading
Coefficient Test
we can determine the end behavior of the graph of our given polynomial:
Since the degree of the polynomial, 4, is even and
the leading
coefficient, -1, is negative, then the graph of the given
polynomial
falls to the left and falls to the right. |
First question is what is the
leading term?
If you said 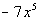 ,
you are correct!! ,
you are correct!!
Second question is what is the leading term’s degree?
If you said 5, you are right on!! 5 is the
exponent on the leading
term, which also means it is the degree of the polynomial.
Third question is what is the coefficient on the
leading term?
If you said -7, pat yourself on the back!!
Putting this information together with the Leading
Coefficient Test
we can determine the end behavior of the graph of our given polynomial:
Since the degree of the polynomial, 5, is odd and
the leading
coefficient, -7, is negative, then the graph of the given
polynomial
rises to the left and falls to the right. |
First question is what is the
leading term?
If you said 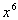 ,
you are correct!! ,
you are correct!!
Second question is what is the leading term’s degree?
If you said 6, you are right on!! 6 is the
exponent on the leading
term, which also means it is the degree of the polynomial.
Third question is what is the coefficient on the
leading term?
If you said 1, pat yourself on the back!!
Putting this information together with the Leading
Coefficient Test
we can determine the end behavior of the graph of our given polynomial:
Since the degree of the polynomial, 6, is even and
the leading
coefficient, 1, is positive, then the graph of the given polynomial
rises to the left and rises to the right. |
|
Zeros (or Roots) of Polynomial
Functions
|
A zero or root of a polynomial function is the value
of x such that f(x)
= 0.
In other words it is the x-intercept,
where
the functional value or y is equal to 0. |
|
Zero of Multiplicity k
If 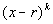 is
a factor of a polynomial function f and is
a factor of a polynomial function f and
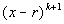 is
not a factor of f, then r is called a zero of is
not a factor of f, then r is called a zero of
multiplicity k of f.
|
In other words, when a polynomial function is set equal
to zero and
has been completely factored and each different factor is written with
the highest appropriate exponent, depending on the number of times that
factor occurs in the product, the exponent on the factor that the zero
is a solution for, gives the multiplicity of that zero.
The exponent indicates how many times that factor would
be written out
in the product, this gives us a multiplicity. |
|
Multiplicity of Zeros and the x-intercept
|
There are two cases that go with this concept:
Case 1:
If r is a zero
of even multiplicity:
This means the graph touches the x-axis
at r and turns around.
This happens because the sign of f(x)
does not change from one side to the other side of r. |
Case 2:
If r is a zero
of odd multiplicity:
This means the graph crosses the x-axis
at r.
This happens because the sign of f(x)
changes from one side to the other side of r. |
|
|
Turning Points
If f is a polynomial function
of degree n,
then
there is at most n - 1
turning points on the
graph of f.
|
A turning point is a point at which the graph
changes direction.
Keep in mind that you can have fewer than n - 1 turning points, but it will never exceed n - 1 turning points. |
 Example
5 Example
5: Find the zeros for the polynomial function 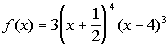 and give the multiplicity for each zero. Indicate whether the
graph
crosses the x-axis or touches the x-axis
and turns around at each zero. |
First Factor:
The first factor is 3, which is a constant.
Therefore, there are
no zeros that go with this factor. |
|
*Setting the 2nd factor = 0
*Solve for x
*x = -1/2 is a
zero
|
What would the multiplicity of the zero x = -1/2 be?
If you said the multiplicity for x =
-1/2 is 4, you are correct!!!! Since the exponent on this
factor
is 4, then its multiplicity is 4.
Does the graph cross the x-axis
or touch
the x-axis and turn around at the zero x = -1/2?
If you said it touches the x-axis
and
turns around at the zero x = -1/2,
pat
yourself on the back!!! It does this because the multiplicity is
4, which is even. |
|
*Setting the 3rd factor = 0
*Solve for x
*x =
4 is a zero |
What would the multiplicity of the zero x = 4 be?
If you said the multiplicity for x =
4 is 3, you are correct!!!! Since the exponent on this factor
is 3, then its multiplicity is 3.
Does the graph cross the x-axis
or touch
the x-axis and turn around at the zero x = 4?
If you said it crosses the x-axis
at
the zero x = 4, pat yourself on the
back!!!
It does this because the multiplicity is 3, which is odd. |
 Example
6 Example
6: Find the zeros for the polynomial function 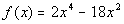 and give the multiplicity for each zero. Indicate whether the
graph
crosses the x-axis or touches the x-axis
and turns around at each zero. |
Let’s factor this one first: |
|
*Setting the 1st factor = 0
*Solve for x
*x =
0 is a zero |
What would the multiplicity of the zero x = 0 be?
If you said the multiplicity for x =
0 is 2, you are correct!!!! Since the exponent on this factor
is 2, then its multiplicity is 2.
Does the graph cross the x-axis
or touch
the x-axis and turn around at the zero x = 0?
If you said it touches the x-axis
and
turns around at the zero x = 0, pat
yourself
on the back!!! It does this because the multiplicity is 2, which
is even. |
|
*Setting the 2nd factor = 0
*Solve for x
*x =
-3 is a zero |
What would the multiplicity of the zero x = -3 be?
If you said the multiplicity for x =
-3 is 1, you are correct!!!! Since the exponent on this
factor
is 1, then its multiplicity is 1.
Does the graph cross the x-axis
or touch
the x-axis and turn around at the zero x = -3?
If you said it crosses the x-axis
at
the zero x = -3, pat yourself on
the back!!!
It does this because the multiplicity is 1, which is odd. |
|
*Setting the 3rd factor = 0
*Solve for x
*x =
3 is a zero |
What would the multiplicity of the zero x = 3 be?
If you said the multiplicity for x =
3 is 1, you are correct!!!! Since the exponent on this factor
is 1, then its multiplicity is 1.
Does the graph cross the x-axis
or touch
the x-axis and turn around at the zero x = 3?
If you said it crosses the x-axis
at
the zero x = 3, pat yourself on the
back!!!
It does this because the multiplicity is 1, which is odd. |
|
Graphing a Polynomial Function
|
Step 1: Determine the
graph’s end behavior. |
Step 2: Find the x-intercepts
or zeros of the function. |
Recall that you find your x-intercept
or
zero by setting your function equal to 0, f(x)
= 0, completely factoring the polynomial and setting each factor equal
to 0.
If you need a review on x-intercepts,
feel
free to go to Tutorial 26:
Equations
of Lines.
Keep in mind that when 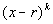 is a factor of your polynomial and
is a factor of your polynomial and
a) if k is even,
the graph touches the x-axis
at r and turns around.
b) if k is odd, the
graph crosses the x-axis
at r. |
|
Step 3: Find the y-intercept
of the function. |
Recall that you can find your y-intercept
by letting x = 0 and find your
functional value
at x = 0, f(0).
If you need a review on y-intercepts,
feel
free to go to Tutorial 26:
Equations
of Lines. |
Step 4: Determine if
there is any symmetry. |
y-axis symmetry:
Recall that your function is symmetric about the y-axis
if it is an even function. In other words, if f(-x)
= f(x),
then your
function is symmetric about the y-axis.
Origin symmetry:
Recall that your function is symmetric about the origin if it is an
odd function. In other words, if
f(-x)
= -f(x),
then your function is symmetric about the origin.
If you need a review on even and odd functions, feel
free to go to Tutorial
32: Graphs of Functions, Part II. |
Step 5: Find the number
of maximum turning points. |
As discussed above, if f is a polynomial
function of degree n, then there is at
most n - 1 turning points on the graph of f. |
Step 6: Find extra points,
if needed. |
Sometimes you may need to find points that are in
between the ones
you found in steps 2 and 3 to help you be more accurate on your graph. |
Plot the points found in steps 2, 3, and 6 and use the
information
gathered in steps 1, 2, 4, and 5 to draw your graph.
The graph of polynomial functions is always a smooth
continuous curve. |
 Example
7 Example
7: Given the polynomial function 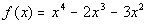
a) use the Leading Coefficient Test to determine the graph’s end
behavior,
b) find the x-intercepts (or zeros) and
state
whether the graph crosses the x-axis or
touches
the x-axis and turns around at each x-intercept,
c) find the y-intercept, d) determine
the symmetry
of the graph, e) indicate the maximum possible turning points, and f)
graph. |
|
Do you think that the graph rises or falls to the
left and to the
right?
Since the degree of the polynomial, 4, is even and
the leading
coefficient, 1, is positive, then the graph of the given polynomial rises
to the left and rises to the right. |
|
*Setting the 1st factor = 0
*Solve for x
*x =
0 is a zero |
Since the exponent on this factor is 2, then the multiplicity
for
the zero x = 0 is 2.
Since the multiplicity is 2, which is even, then the
graph touches
the x-axis and turns around at the zero x = 0. |
|
*Setting the 2nd factor = 0
*Solve for x
*x =
3 is a zero |
Since the exponent on this factor is 1, then the multiplicity
for
the zero x = 3 is 1.
Since the multiplicity is 1, which is odd, then the
graph crosses
the x-axis at the zero x = 3. |
|
*Setting the 3rd factor = 0
*Solve for x
*x =
-1 is a zero |
Since the exponent on this factor is 1, then the
multiplicity for the
zero x = -1 is 1.
Since the multiplicity is 1, which is odd, then the
graph crosses the x-axis
at the zero x = -1. |
The y-intercept is
(0, 0). |
Step 4: Determine if
there is any symmetry. |
It is not symmetric about the y-axis. |
|
*Plug in -x for x
*Take the opposite of f(x)
|
It is not symmetric about the origin. |
Since the degree of the function is 4, then there is at
most 4 -
1 = 3 turning points. |
To get a more accurate curve, lets find some points
that are in between
the points we found in steps 2 and 3: |
|
x
|
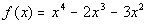
|
(x, y)
|
|
-.5
|
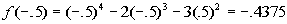
|
(-.5, -.437)
|
|
1
|
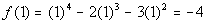
|
(1, -4)
|
|
2
|
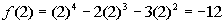
|
(2, -12)
|
 Example
8 Example
8: Given the polynomial function 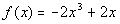
a) use the Leading Coefficient Test to determine the graph’s end
behavior,
b) find the x-intercepts (or zeros) and
state
whether the graph crosses the x-axis or
touches
the x-axis and turns around at each x-intercept,
c) find the y-intercept, d) determine
the symmetry
of the graph, e) indicate the maximum possible turning points, and f)
graph. |
|
Do you think that the graph rises or falls to the
left and to the
right?
Since the degree of the polynomial, 3, is odd and
the leading
coefficient, -2, is negative, then the graph of the given polynomial rises
to the left and falls to the right. |
|
*Setting the 1st factor = 0
*Solve for x
*x =
0 is a zero |
Since the exponent on this factor is 1, then the multiplicity
for
the zero x = 0 is 1.
Since the multiplicity is 1, which is odd, then the graph crosses
the x-axis at the zero x = 0. |
|
*Setting the 2nd factor = 0
*Solve for x
*x =
-1 is a zero |
Since the exponent on this factor is 1, then the multiplicity
for
the zero x = -1 is 1.
Since the multiplicity is 1, which is odd, then the
graph crosses
the x-axis at the zero x = -1. |
|
*Setting the 3rd factor = 0
*Solve for x
*x =
1 is a zero |
Since the exponent on this factor is 1, then the
multiplicity for the
zero x = 1 is 1.
Since the multiplicity is 1, which is odd, then the
graph crosses the x-axis
at the zero x = 1. |
The y-intercept is
(0, 0). |
Step 4: Determine if
there is any symmetry. |
It is not symmetric about the y-axis. |
|
*Plug in -x for x
*Take the opposite of f(x)
|
It is symmetric about the origin. |
Since the degree of the function is 3, then there is at
most 3 -
1 = 2 turning points. |
To get a more accurate curve, lets find some points
that are in between
the points we found in steps 2 and 3: |
|
x
|
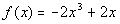
|
(x, y)
|
|
-1/2
|
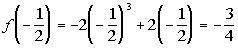
|
(-1/2, -3/4)
|
|
1/2
|
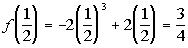
|
(1/2, 3/4)
|
 Practice Problems Practice Problems
These are practice problems to help bring you to the next level.
It will allow you to check and see if you have an understanding of these
types of problems. Math works just like anything
else, if you want to get good at it, then you need to practice it.
Even the best athletes and musicians had help along the way and lots of
practice, practice, practice, to get good at their sport or instrument.
In fact there is no such thing as too much practice. To get the most out of these, you should work the problem out on
your own and then check your answer by clicking on the link for the answer/discussion
for that problem. At the link you will find the answer
as well as any steps that went into finding that answer. |
 Practice
Problems 1a - 1b: Given the polynomial function
a) use the Leading
Coefficient Test to determine the graph’s end behavior, b) find the x-intercepts
(or zeros) and state whether the graph crosses the x-axis or
touches
the x-axis and turns around at each x-intercept, c)
find
the y-intercept, d) determine the symmetry of the graph, e)
indicate
the maximum possible turning points, and f) graph. Practice
Problems 1a - 1b: Given the polynomial function
a) use the Leading
Coefficient Test to determine the graph’s end behavior, b) find the x-intercepts
(or zeros) and state whether the graph crosses the x-axis or
touches
the x-axis and turns around at each x-intercept, c)
find
the y-intercept, d) determine the symmetry of the graph, e)
indicate
the maximum possible turning points, and f) graph.
 Need Extra Help on these Topics? Need Extra Help on these Topics?

Last revised on March 14, 2012 by Kim Seward.
All contents copyright (C) 2002 - 2012, WTAMU and Kim Seward. All rights reserved.
|
|


