College Algebra
Tutorial 26: Equations of Lines
 Learning Objectives
After completing this tutorial, you should be able to:
- Know what x- and y-intercepts
are.
- Use the point/slope equation to set up an equation given any point on
the
line and the slope.
- Use the point/slope equation to set up an equation given two points on
the line.
- Write a linear equation in the slope/intercept form.
|
Introduction
In this tutorial we will look closer at equations of
straight lines.
We
will be going over how to come up with our own equations given certain
information. We will be using the slope of the line and a point
it
passes through to do this. If you need a review on the slope of a
line, feel free to go to Tutorial
25: Slope of a Line. We will also be going over the
concepts
of x- and y-intercepts.
After you finish tutorials 25 - 28, you will be an old pro at
linear
equations and graphing. Let's see what we can do with x-
and y-intercepts and linear
equations. |
Tutorial
The x-intercept is
where the graph crosses
the x axis.
The word 'intercept' looks like the word
'intersect'. Think
of it as where the graph intersects the x-axis.
With that in mind, what
value is y always going to be on the x-intercept?
No matter where you are on the x-axis, y’s
value is 0, that is a constant. We will use that
bit of information to help us find the x-intercept. |
If the x-intercept is
where the graph crosses
the x-axis where do you think the
graph
crosses for the y-intercept?
If you
said the y-axis, you are
absolutely
right.
This time it is x’s
value that is 0. Anywhere you would cross the y-axis, x’s
value is always 0. We will use this tidbit to help us find the y-intercept.
Below is an illustration of a graph of a linear function
which highlights
the x and y intercepts:
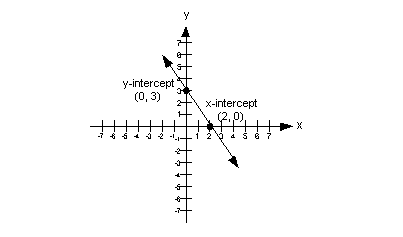
In the above illustration, the x-intercept
is the point (2, 0) and the y-intercept
is the point (0, 3).
Keep in mind that the x- and y- intercepts are two separate
points. There
is only one point that can be both an x- and y- intercept at the same time, do you know what point that is?
If you said the origin, (0, 0), give yourself a
pat on the back. |
|
Point/Slope Form of an Equation
A line going through
the point 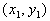 and having slope of m
would have the equation
|
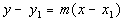
We can use this form to plug into when we need to
come up with a
linear equation.
When writing an equation of a line, keep in mind that you
ALWAYS need two pieces of information when you go to write an equation:
- ANY point on the line
- Slope
Once you have these two pieces of
information,
you plug the x and y values from your point and the slope (m)
value
into the point/slope formula. |
|
Slope/Intercept Equation of a
Line
|
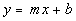
In this form, m represents the slope
and b represents the y-intercept
of the line.
Sometimes the directions will say to write the equation
in the slope/intercept
form. Basically this means to solve the equation for y.
Note how y is by itself and everything
else
is on the other side. Most times you will need to start the
problem
using the point/slope form and then you just solve for y to get it into the slope/intercept form. Sometimes if you have it
written in this form it makes it easier to work with when you graph. |
 Example
1: Write an equation for the line in point/slope form
and slope/intercept form that has slope = -5 and passes through (2, 1).
 View a video of this example
|
What are the two things we need to write an equation
of a line????
If you said any point on the line and the slope, you are
correct.
Looks like we have all the information we need. We
are ready to
put our equation together.
Point/Slope Form: |
|
*Point/slope form of the line |
Next, we want to write it in the Slope/Intercept
Form, which basically means we need to solve for y: |
|
*Dist. the -5 through ( )
*Inverse of sub. 1 is add 1
*Slope/intercept form of the
line |
The equation of the line that passes through (2, 1)
and has a slope
of -5 is
y - 1 = -5(x - 2) OR y=
-5x + 11. |
Example
2: Write an equation for the line in point/slope form
and slope/intercept form that has slope = 3 and passes through the
origin.
View a video of this example
|
What are the two things we need to write an equation
of a line????
If you said any point on the line and the slope, you are
correct.
Do you know what the ordered pair for the origin is?
If
you said (0, 0) you are right on!!! That is the point that we
will
be using to plug into our equation.
Looks like we have all the information we need. We
are ready to
put our equation together.
Point/Slope Form: |
|
*Point/slope form of the line |
Next, we want to write it in the Slope/Intercept
Form, which basically means we need to solve for y: |
|
*Dist. the 3 through ( )
*Slope/intercept form of the line |
The equation of the line that passes through the
origin and has
a slope of 3 is
y - 0 = 3(x - 0) OR y = 3x. |
Example
3: Write an equation for the line in point/slope form
and slope/intercept form that passes through (-2, 1) and (2, 2).
View a video of this example
|
What are the two things we need to write an equation
of a line????
If you said any point on the line and the slope, you are
correct.
We have more than enough points. However, what about the
slope?
Does this mean we can’t work out the problem? You are not going
to
get off that easily. We do have a way of finding the slope. Tutorial
25: The Slope of a Line shows us how we can get the slope given two
points.
Let’s find that slope: |
|
*Slope formula
*Plug in values
*Simplify
|
OK, now we have our slope, which is 1/4.
Now it is just like examples 1 and 2 above, we want to put
the slope
and one point into the point/slope equation. Note that you
can
use either point to plug in as long as it is a point that the line
passes
through. I chose to plug in the point (-2, 1).
Point/Slope Form: |
|
*Point/slope form of the line
|
Make sure that you are careful when one of your
values is negative
and you have to subtract it as we did in line 2. x - (-2) is not the same as x - 2. |
Next, we want to write it in the Slope/Intercept
Form, which basically means we need to solve for y: |
|
*Dist. the 1/4 through (
)
*Inverse of sub. 1 is add 1
*Slope/intercept form of the
line |
The equation of the line that passes through the
points (-2, 1)
and (2, 2) is
y - 1 = 1/4(x + 2) OR y = 1/4x + 3/2. |
Example
4: Write an equation for the line in point/slope form
and slope/intercept form that has an x-intercept
of -2 and y-intercept of 1.
View a video of this example
|
What are the two things we need to write an equation
of a line????
If you said any point on the line and the slope, you are
correct.
Do you know what the ordered pair is going to be for
the x-intercept?
What about the y-intercept?
Above, we leaned that an x-intercept is where the line crosses the x-axis.
That means y’s value is always 0.
So
the ordered pair for our x-intercept is
(-2.
0).
Above, we learned that an y-intercept is where the line crosses the y-axis.
That means x’s value is always 0.
So
the ordered pair for our y-intercept is
(0,
1).
We have more than enough points. However, what about the
slope?
Does this mean we can’t work out the problem? You are not going
to
get off that easily. We do have a way of finding the slope. Tutorial
25: The Slope of a Line shows us how we can get the slope given two
points.
Let’s find that slope: |
|
*Slope formula
*Plug in values
*Simplify
|
OK, now we have our slope, which is 1/2.
Now it is just like examples 1 and 2 above, we want to put
the slope
and one point into the point/slope equation. Note that you
can
use either point to plug in as long as it is a point that the line
passes
through. I chose to plug in the point (-2, 0).
Point/Slope Form: |
|
*Point/slope form of the line
|
Make sure that you are careful
when one of
your values is negative and you have to subtract it as we did in line
2. x - (-2) is not the same as x - 2. |
Next, we want to write it in the Slope/Intercept
Form, which basically means we need to solve for y: |
|
*Dist. the 1/2 through (
)
*Slope/intercept form of the
line |
The equation of the line that has an x-intercept
of -2 and y-intercept of 1 is
y - 0 = 1/2(x + 2) OR y = 1/2x + 1. |
Practice Problems
These are practice problems to help bring you to the next level.
It will allow you to check and see if you have an understanding of these
types of problems. Math works just like anything
else, if you want to get good at it, then you need to practice it.
Even the best athletes and musicians had help along the way and lots of
practice, practice, practice, to get good at their sport or instrument.
In fact there is no such thing as too much practice. To get the most out of these, you should work the problem out on
your own and then check your answer by clicking on the link for the answer/discussion
for that problem. At the link you will find the answer
as well as any steps that went into finding that answer. |
 Practice
Problems 1a - 1c: Write an equation for the line in
point/slope form
and slope/intercept form that has the given condition.
Need Extra Help on these Topics?
Last revised on Feb. 6, 2010 by Kim Seward.
All contents copyright (C) 2002 - 2010, WTAMU and Kim Seward. All rights reserved.
|
|
