GRE Math Practice Test II
Answer Key with Explanations
P. 3 (Problems 20 - 28)
Answer:
E
The distance/rate formula is 
.
In this problem we have the distance and the time and we are looking for the rate.
Plugging in 500 for distance and 8 for time into the distance/rate formula we get:
Need more help on these topics? Word Problems
Answer: D
The distance/rate formula is .
In both parts we have the rate and the time and we are needing to find the distance traveled.
Plugging in 75 for rate and 9 for time into the distance/rate formula we get:
Plugging in 60 for rate and 7 for time into the distance/rate formula we get:
Putting these two trips together we get: 675 + 420 = 1095.
Courtney traveled a total of 1095 miles.
Need more help on these topics? Word Problems
Answer: D
The distance/rate formula is .
This problem has several parts to it.
First let see how many miles Carly traveled overall. Plugging in the rate of 50 mph and the time of 8 hours we get:
Carly traveled a total of 400 miles.
Next we start breaking it down. It says that she traveled for 6 hours at 55 mph. From this we can figure out how many of the 400 miles she traveled at this speed:
She traveled 330 miles at the 55 mph.
How many miles does that leave us for the unknown
speed?
400 - 330 = 70
For the last part, we are again going to use the distance/rate formula, but now we are looking for the rate. Plugging in 70 for the distance and 2 for the time we get:
Need more help on these topics? Word Problems
Answer: C
The distance/rate formula is .
On this problem we will need to see what the total time and total distance traveled were and then find the rate from there.
He traveled a total of 280 + 390 = 670 miles.
It took him a total of 4 + 6 = 10 hours to travel.
Plugging in 670 for distance and 10 for time into the distance/rate formula we get:
Need more help on these topics? Word Problems
Answer: E
The distance/rate formula is .
On this problem we will need to see what the total time and total distance traveled were and then find the rate from there.
He traveled a total of 500 + 480 + 455 = 1435 miles.
It took him a total of 10 + 8 + 7 = 25 hours to travel.
Plugging in 1435 for distance and 25 for time into the distance/rate formula we get:
Need more help on these topics? Word Problems
Answer:
B
Ultimately, we need to find the area of the circle. That
means we need the area of a circle formula which is 
.
Since we were not given the radius of the circle, it looks like we will have to go out and find it.
Since the area of a square is found by taking the side squared, this means the side of our square is going to be 12 cm, since its area is 144 square cm.
Let's look at a visual of this:
It looks like the side of the square is also the diameter of the circle. Since the diameter is 12, the radius, which is half of the diameter, is going to be 12/2 or 6.
Putting the radius into the area formula we get:
The area of the circle is 
square cm.
Need more help on these topics? Formulas for Two-Dimensional Figures and Inscribed Figures
Answer: E
Ultimately, we need to find the area of the circle. That
means we need the area of a circle formula which is .
Since we were not given the radius of the circle, it looks like we will have to go out and find it.
Since the area of a square is found by taking the side squared, this means the side of our square is going to be 10 cm, since its area is 100 square cm.
Let's look at a visual of this:
It looks like the side of the square is also the diameter of the circle. Since the diameter is 10, the radius, which is half of the diameter, is going to be 10/2 or 5.
Putting the radius into the area formula we get:
The area of the circle is approximately 78.5 square cm.
Need more help on these topics? Formulas for Two-Dimensional Figures and Inscribed Figures
Answer:
A
Ultimately, we need to find the area of the circle. That
means we need the area of a circle formula which is .
Since we were not given the radius of the circle, it looks like we will have to go out and find it.
Since the area of a square is found by taking the side squared, this means the side of our square is going to be 11 cm, since its area is 121 square cm.
Let's look at a visual of this:
It looks like the side of the square is also the diameter of the circle. Since the diameter is 11, the radius, which is half of the diameter, is going to be 11/2 or 5.5.
Putting the radius into the area formula we get:
The area of the circle is approximately 95 square cm.
Need more help on these topics? Formulas for Two-Dimensional Figures and Inscribed Figures
square feet?Answer:
B
Ultimately, we need to find the area of the square. That
means we need the area of a square formula which is 
.
Since we were not given the side of the square, it looks like we will have to go out and find it.
Since the area of a circle is found by taking pi times
the radius squared, this means the radius of our circle is going to be 5 feet,
since its area is
square feet.
Let's look at a visual of this:
Just a reminder that all four sides of a square are equal and
the diagonal of a square is equal to 
.
Putting 10 in the diagonal we get:
*Square root method
feet long. Putting in
into the area formula we get:
The area of the square is 50 square feet.
Need more help on these topics? Formulas for Two-Dimensional Figures and Inscribed Figures
square feet?Answer:
B
Ultimately, we need to find the area of the square. That
means we need the area of a square formula which is .
Since we were not given the side of the square, it looks like we will have to go out and find it.
Since the area of a circle is found by taking pi times
the radius squared, this means the radius of our circle is going to be 2 feet,
since its area is
square feet.
Let's look at a visual of this:
It looks like the diameter of the circle is the diagonal of the square.
Just a reminder that all four sides of a square are equal and
the diagonal
of a square is equal to .
Putting 4 in the diagonal we get:
*Square root method
feet long. Putting in
into the area formula we get:
The area of the square is 8 square feet.
Need more help on these topics? Formulas for Two-Dimensional Figures and Inscribed Figures
Answer:
A
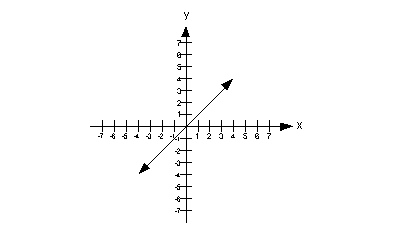
The slope can be found by using rise/run. I prefer to go left to right. I’m going to start with the point that is on the x-axis, which is (0, 0) and then step up to the point (1, 1). If we do that, we rise up 1 and go over to the right 1.
So the slope is rise/run which is 1/1 = 1.
The x-intercept is the point where the graph crosses the x-axis. In this case that is (0, 0). The x-value of that point is 0.
This means that the slope is greater than the x
value of the x-intercept.
Need more help on these topics? Coordinate Geometry
Answer:
B
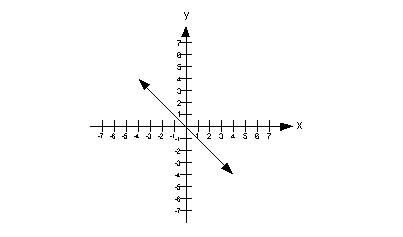
The slope can be found by using rise/run. I prefer to go left to right. I’m going to start with the point that is on the x-axis, which is (0, 0) and then step down to the point (1, -1). If we do that, we “rise” down 1 and go over to the right 1.
So the slope is rise/run which is -1/1 = -1.
The x-intercept is the point where the graph crosses the x-axis. In this case that is (0, 0). The x-value of that point is 0.
This means that the x value
of the x-intercept
is greater than the slope of the line.
Need more help on these topics? Coordinate Geometry
Answer:
A
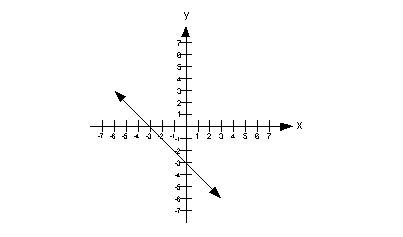
The slope can be found by using rise/run. I prefer to go left to right. I’m going to start with the point that is on the x-axis, which is (-3, 0) and then step down to the point (0, -3). If we do that, we “rise” down 3 and go over to the right 3.
So the slope is rise/run which is -3/3 = -1.
The x-intercept is the point where the graph crosses the x-axis. In this case that is (-3, 0). The x-value of that point is -3.
This means that the slope of the line is greater than the x
value of the x-intercept.
Need more help on these topics? Coordinate Geometry
Answer: B
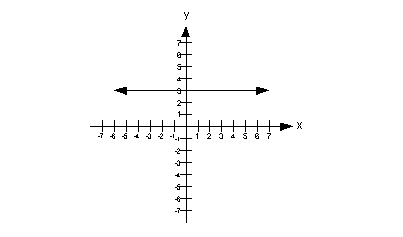
Since the line is a horizontal line, this means the slope of this line is 0.
The y-intercept is the point where the graph crosses the y-axis. In this case that is (0, 3). The y-value of that point is 3.
This means that the y value
of the y-intercept is greater than the slope of the line.
Need more help on these topics? Coordinate Geometry
Answer:
A
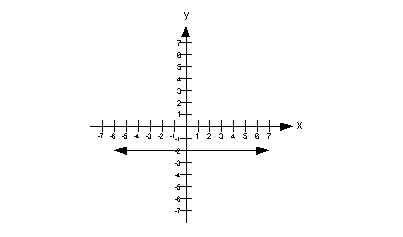
Since the line is a horizontal line, this means the slope of this line is 0.
The y-intercept is the point where the graph crosses the y-axis. In this case that is (0, -2). The y-value of that point is -2.
This means that the slope of the line is greater than the y
value of the y-intercept.
Need more help on these topics? Coordinate Geometry
Answer:
C
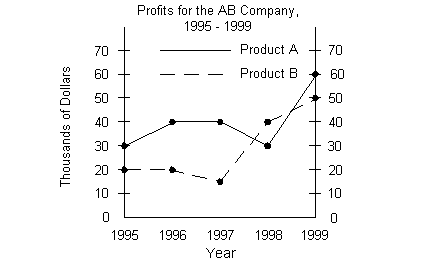
Taking the difference between the profits for Product A and Product B in the year 1996 we would get:
40 - 20 = 20
Keeping in mind that the profit is in thousands of dollars, this
difference would be $20,000.
To find the median of the profits for 1995 to 1999 for Product B, we want to first list the profits for each year from smallest to largest: 10, 20, 20, 40, 50.
The median is the middle value, which in this case would be 20. Since the profit is in thousand of dollars, it would be $20,000.
The difference of profits between Product A and Product B
in the
year 1996 would be the same as the median of all of the profits for
1995
to 1999 for Product B.
Need more help on these topics? Central Tendencies and Reading Graphs
Answer:
B
Taking the difference between the profits for Product A and Product B in the year 1996 we would get:
40 - 20 = 20
Keeping in mind that the profit is in thousands of dollars, this difference would be $20,000.
To find the mean we need to sum the profits for Product B and then divide by 5:
Keeping in mind that the profit is int thousands of dollars,
the mean would be $29,000.
The mean of all of the profits for 1995 to 1999 for Product
B is greater than the difference of profits between Product A and Product B
in the year 1996.
Need more help on these topics? Central Tendencies and Reading Graphs
Answer: B
To find the median of the profits for 1995 to 1999 for Product B, we want to first list the profits for each year from smallest to largest: 10, 20, 20, 40, 50
The median is the middle value, which in this case would be 20. Since the profit is in thousand of dollars, it would be $20,000.
To find the mean we need to sum the profits for Product B and then divide by 5:
Keeping in mind that the profit is in thousands of dollars,
the mean would be $29,000.
The mean of all of the profits for 1995 to 1999 for Product
B is greater than the median of all of the profits for 1995 to 1999 for
Product B.
Need more help on these topics? Central Tendencies and Reading Graphs
Answer:
B
The mode is the value that occurs most often. For product B, it looks like the profit was $20,000 for two years and all of the values for profit occurred only once. The mode is $20,000.
To find the mean we need to sum the profits for Product B and then divide by 5:
Keeping in mind that the profit is in thousands of dollars, the mean would be $29,000.
The mean of all of the profits for 1995 to 1999 for Product
B is greater than the mode of all of the profits for 1995 to 1999 for
Product B.
Need more help on these topics? Central Tendencies and Reading Graphs
Answer:
D
The mode is the value that occurs most often. For product A, it looks like the profit of $30,000 AND $40,000 both occur for two years. The mode is $30,000 and $40,000.
To find the mean we need to sum the profits for Product A and then divide by 5:
Keeping in mind that the profit is int thousands of dollars, the mean would be $40,000.
Since the mode of the profits of Product A can be either
$30,000 or $40,000, and the mean for the profits of Product A is $40,000, we
cannot determine the relationship.
Need more help on these topics? Central Tendencies and Reading Graphs
For what year shown did the profits of Product A exceed the profits of Product B by the greatest number?
Answer:
C
It looks like the biggest difference between the profits of
Product A (solid line) and Product B (dashed line), where A exceeded B,
was $40,000 - $15,000 = $30,000 in 1997.
Need more help on these topics? Reading Graphs
What was the total profits of Product B from 1995 to 1998?
Answer:
E
Since we are looking at the profits for Product B, we need to look at the dashed line.
Adding up the profits of Product B from 1995 to 1998 we get:
$20,000 + $20,000 + $15,000 + $40,000 = $95,000
Need more help on these topics? Reading Graphs
What was the difference in total profits between Product A from 1995 to 1999 and Product B from 1995 to 1999?
Answer:
D
Adding up the profits of Product A (solid line) from 1995 to 1999 we get:
$30,000 + $40,000 + $40,000 + $30,000 + $60,000 = $200,000
Adding up the profits of Product B (dashed line) from 1995 to 1999 we get:
$20,000 + $20,000 + $15,000 + $40,000 + $50,000 = $145,000
Taking their difference we get $200,000 - $145,000 = $55,000
Need more help on these topics? Reading Graphs
The percent increase in profits for Product A from 1995 to 1996 was approximately what %?
Answer:
A
Since we are looking at the increase in profits for Product A, we need to look at the solid line.
1995 had a profit of $30,000 and 1996 had a profit of $40,000.
We are needing to find the percent increase in profits for Product A from 1995 to 1996. First lets see what the increase in dollar amount was:
$40,000 - $30,000 = $10,000
There was a $10,000 increase in profits from 1995 to 1996. From this we need to find out what percent 10,000 is of 30,000, since that is the amount we are increasing from:
$10,000 is approximately 33% of $30,000.
Need more help on these topics? Percents and Reading Graphs
The percent decrease in profits for Product A from 1997 to 1998 was approximately what %?
Answer: A
Since we are looking at the decrease in profits for Product A, we need to look at the solid line.
1997 had a profit of $40,000 and 1998 had a profit of $30,000.
We are needing to find the percent decrease in profits for Product A from 1997 to 1998. First lets see what the decrease in dollar amount was:
$40,000 - $30,000 = $10,000
There was a $10,000 decrease in profits from 1997 to 1998. From this we need to find out what percent 10,000 is of 40,000, since that is the amount we are decreasing from:
$10,000 is 25% of $40,000.
Need more help on these topics? Percents and Reading Graphs
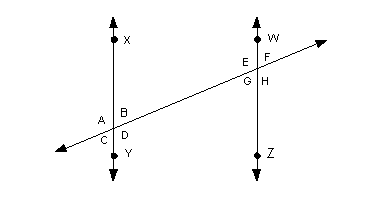
Given that line XY is parallel to line WZ and angle A is 105 degrees, what is the measurement of angle H in degrees?
Answer:
A
Since line XY is parallel to line WZ, then the measurements of angle A and angle E are equal to each other because they are corresponding angles.
The measurements of angles E and H are also equal to each other because they are vertical angles.
Hence, angle H also equals 105 degrees.
Need more help on these topics? Basic Geometry
Given that line XY is parallel to line WZ and angle A is 105 degrees, what is the measurement of the sum of angles C and H in degrees?
Answer: D
First, we need to find the measurements of angles C and H.
Since angles C and A make a straight angle, their sum is 180 degrees. Well, if angle A is 105 degrees, then angle C would have to be 180 - 105 = 75 degrees.
Since line XY is parallel to line WZ, then the measurements of angle A and angle E are equal to each other because they are corresponding angles. The measurements of angles E and H are also equal to each other because they are vertical angles. Hence, angle H also equals 105 degrees.
Summing up the measurements of angles C and H we get: 75 + 105 = 180.
The sum of angles C and H is 180 degrees.
Need more help on these topics? Basic Geometry
Given that line XY is parallel to line WZ and angle A is 105 degrees, what is the relationship between the measurements of angle F and angle D?
Answer:
D
Since line XY is parallel to line WZ, then the measurements of angle F and angle B are equal to each other because they are corresponding angles. Angles B and D make up a straight angle, so their sum is 180 degrees.
Since the measurement of angle F is the same as angle B, then
the sum
of the measurements of angles F and D is also 180 degrees.
Need more help on these topics? Basic Geometry
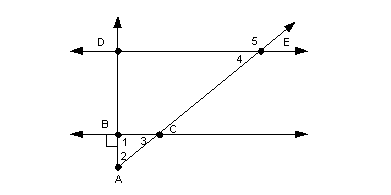
Given that line DE is parallel to line BC, angle 2 is equal to angle 3, and angle 1 is a right angle, what is the measure of angle 5 in degrees?
Answer:
C
Since triangle ABC is a right triangle, angles 2 and 3 are equal, and the three angles of a triangle sum up to be 180 degrees, then angles 2 and 3 are both 45 degrees.
Since line DE is parallel to line BC, then the measurements of angle 3 and angle 4 are equal to each other because they are corresponding angles. Angles 4 and 5 make up a straight angle, so their sum is 180 degrees. SO this means angles 3 and 5 would also sum up to be 180 degrees.
So angle 5 would be 180 - 45 = 135 degrees.
Need more help on these topics? Basic Geometry
Given that line DE is parallel to line BC, angle 2 is equal to angle 3, and angle 1 is a right angle. What is the sum of the measures of angles 3, 4, and 5 in degrees?
Answer: D
Since triangle ABC is a right triangle, angles 2 and 3 are equal, and the three angles of a triangle sum up to be 180 degrees, then angles 2 and 3 are both 45 degrees.
Since line DE is parallel to line BC, then the measurements of angle 3 and angle 4 are equal to each other because they are corresponding angles. So angle 4 would also be 45 degrees.
Angles 4 and 5 make up a straight angle, so their sum is 180 degrees. So this means angle 5 would be 180 - 45 = 135.
Now we can sum up all of our angles: 45 + 45 + 135 = 225.
The sum of the measures of angles 3, 4, and 5 is 225
degrees.
Need more help on these topics? Basic Geometry
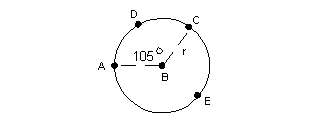
If B is the center of the given circle above, what is the measurement in degrees of arc AEC?
Answer:
D
On this problem, the key is to know that a circle measures 360 degrees.
If arc ADC is 105 degrees, then arc AEC is 360 - 105 = 255
degrees.
Need more help on these topics? Basic Geometry
If B is the center of the given circle above, approximately what percent of the outer circle does arc ADC represent?
Answer:
C
On this problem, the key is to know that a circle measures 360 degrees.
To find the percent we would take ADC’s arc measurement which is 105 degrees and put it over the whole circle’s measurement which is 360 degrees:
Arc ADC represents approximately 29% of the given circle.
Need more help on these topics? Basic Geometry
If B is the center of the given circle above, approximately what percent of the outer circle does arc AEC represent?
Answer:
D
On this problem, the key is to know that a circle measures 360 degrees.
If arc ADC is 105 degrees, then arc AEC is 360 - 105 = 255 degrees.
To find the percent we would take AEC’s arc measurement which is 255 degrees and put it over the whole circle’s measurement which is 360 degrees:
Arc AEC represents approximately 71% of the given circle.
Need more help on these topics? Basic Geometry
If B is the center of the given circle above and the radius is r, what is the circumference of arc ADC in radians?
Answer:
D
On this problem, the key is to know that a circle measures 360 degrees.
We also need to know that the formula for the circumference of
a circle
is 
.
Arc ADC measures 105 degrees out of 360 degrees. This will give us the fraction of the circle we are looking at.
Taking the fraction times the circumference formula we have:
The circumference of arc ADC is 
.
Need more help on these topics? Basic Geometry and Formulas for Two-Dimensional Figures
If B is the center of the given circle above and the radius is r, what is the circumference of arc AEC in radians?
Answer:
D
On this problem, the key is to know that a circle measures 360 degrees.
If arc ADC is 105 degrees, then arc AEC is 360 - 105 = 255 degrees.
We also need to know that the formula for the circumference of
a circle
is .
Arc AEC measures 255 degrees out of 360 degrees. This will give us the fraction of the circle we are looking at.
Taking the fraction times the circumference formula we have:
The circumference of arc AEC is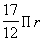 
.
Need more help on these topics? Basic Geometry and Formulas for Two-Dimensional Figures
Answer:
C
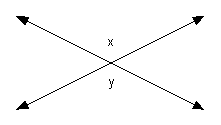
Since x and y
are vertical angles they are equal to each other.
Need more help on these topics? Basic Geometry
Answer:
C
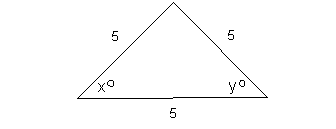
Since all three sides of the triangle are equal, this means
this is
an equilateral triangle, which means angles x
and y are equal to each other.
Need more help on these topics? Basic Geometry
Answer:
B
An octagon has eight sides.
The number of diagonals of a n-sided polygon is
Plugging in 8 for n we get:
There are 20 diagonals in a octagon.
The number of diagonals in an octagon is greater than the
number
of sides of an octagon.
Need more help on these topics? Basic Geometry
Answer:
A
The formula for the area of a rectangle is
Plugging in 5 for width and 30 for area we get:
The length of the rectangle is 6.
The formula for the perimeter of a rectangle is
Plugging in 5 for width and 6 for length we get:
The area of the rectangle is greater than the perimeter of the
rectangle.
Need more help on these topics? Formulas for Two-Dimensional Figures
Answer:
B
The formula for the area of a rectangle is
Plugging in 4 for length and 12 for area we get:
The width of the rectangle is 3.
The formula for the perimeter of a rectangle is
Plugging in 3 for width and 4 for length we get:
The perimeter of the rectangle is greater than the area of the
rectangle.
Need more help on these topics? Formulas for Two-Dimensional Figures
and 
Answer:
A
Plugging in -5 for y we get:
and
Answer:
B
Plugging in -2 for y we get:
and 
Answer:
A
Plugging in -1 for y we get:
and 
Answer:
A
Plugging in -1 for y we get:
and 
Answer:
B
Plugging in -1 for y we get:
WTAMU > Virtual Math Lab > GRE Math
Disclaimer:
Note that we can not
guarantee that you will pass your test after going through any of the tutorials
in this website. However, it will definitely help you to better
understand the topics covered. WTAMU and Kim Seward are not responsible
for how a student does on any test for any reason including not being able
to access the website due to any technology problems.
GRE and Graduate Record Examination are the registered trademarks of Educational Testing Service (ETS). The material here has neither been reviewed nor endorsed by ETS.
Throughout this website, we link to various outside sources. WTAMU and Kim Seward do not have any ownership to any of these outside websites and cannot give you permission to make any kind of copies of anything found at any of these websites that we link to. It is purely for you to link to for information or fun as you go through the study session. Each of these websites have a copy right clause that you need to read carefully if you are wanting to do anything other than go to the website and read it. We discourage any illegal use of the webpages found at these sites.