GRE Math Practice Test II
Answer Key with Explanations
P. 2 (Problems 10 - 19)
WTAMU > Virtual Math Lab > GRE Math
Because of the enormity of this
part, I split the answer/discussion into three pages. P. 1 has the answer/explanations to all levels of the first 9 problems.
This page, P. 2, has the answer/explanations to all levels of problems
10 - 19. P. 3
has the answer/explanations to all levels of problems 20 - 28.
This page also has links to the
mathematical area(s) that each question comes from in case you need to
go back and review.
Printing
warning: Note that because of all of the levels per problem,
there are a lot of questions on this page. So if you wish to
print this out, note that there will be a lot
of pages to print.
|
Column A
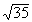 |
Column B
6 |
 Answer:
B Answer:
B
Since the square root of 36 is 6, then 6 is greater
than 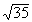 . .
Need more help on these topics? Square
Root
|
Column A
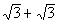 |
Column B
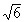 |
 Answer:
A Answer:
A
Since you will not be able to use a calculator on the test,
let me show
you how you can solve this algebraically. I'm going to
rewrite
Column A so that it is under one radical:
|
|
*Add like radicals
*2 is the same as square root of 4
|
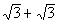 is
greater than 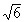 .
Need more help on these topics? Square
Root
|
Column A
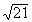 |
Column B
 |
 Answer:
B Answer:
B
Since you will not be able to use a calculator on the test,
let me show
you how you can solve this algebraically. I'm going to
rewrite
Column B so that it is under one radical:
|
|
*2 is the same as square root of 4
|
 is
greater than 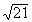 .
Need more help on these topics? Square
Root
|
Column A
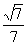 |
Column B
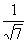 |
 Answer:
C Answer:
C
Rationalizing the denominator in Column B we get:
|
|
*Multiply num. and den. by sq. root of 7
|
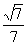 is
equal to 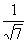 .
Need more help on these topics? Square
Root
|
Column A
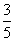 |
Column B
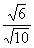 |
 Answer: B Answer: B
Rewriting Column B we get:
|
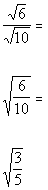
Approx. .775
|
*Simplify the fraction |
Since 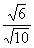 is approximately .775 and 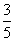 = .6, 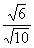 has
a greater
value than 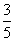 .
Need more help on these topics? Square
Root
|
11 - 1.
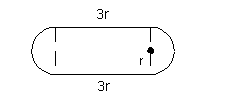
If the radius of the equal semicircles is r
and the length of the rectangle is 3 r,
which
of these expressions represents the perimeter of this object? |
 Answer:
B Answer:
B
Since we need to find the perimeter, we need to find the
measurement
around the figure.
The two straight lines each have a measurement of 3r,
for a total of 6r.
The other part of the figure is two semicircles. These
two parts
make a one whole circle. The circumference of a circle
is
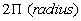
Plugging in r for radius we
have:
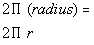
Adding all of the parts together we get:
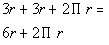
The perimeter of this figure is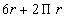 . .
Need more help on these topics? Formulas
for Two-Dimensional Figures
|
11 - 2.
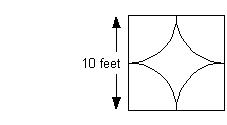
Using the figure shown, find the area of the middle region inside the
square. |
 Answer:
D Answer:
D
Since part of the problem involves the area of a square,
we can
use the formula :
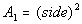
Plugging in 10 for the side we get the following area for
the square:
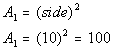
Since part of the problem involves the area of a circle,
we can
use also use the formula:
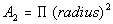
Plugging in 5 for the radius we get the following area for
the four
quarter circles (whole circle):
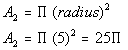
In this problem, if we take the area of the square and
subtract
out the area of the four quarter circles (whole circle), we will have
the
area of the middle region of the given figure above:
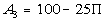
The area of the middle region is 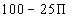 . .
Need more help on these topics? Formulas
for Two-Dimensional Figures
|
11 - 3.
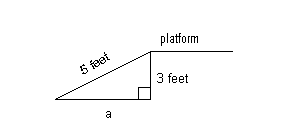
A ramp 5 feet long is leaning against a raised platform which
is 3 feet
above the ground. What is the distance from the ramp’s contact point
with
the ground and the base of the platform?
|
 Answer:
B Answer:
B
Anytime you are missing one side of a right triangle, you can
use the Pythagorean
theorem to find that long lost side:
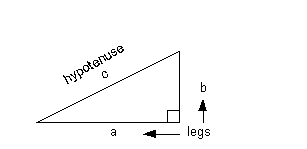
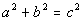
The variables in this formula represent the following:
a and b
= legs
of the right triangle
c = hypotenuse of the right
triangle
In this problem,
a = ? = this is the variable we are
looking
for
b = 3
c = 5
Plugging these values into the formula and solving for a
we get:
|
|
*Plug in 3 for b
and 5 for c
*Inv. of add 9 is sub. 9
*Square root method
|
Since a represents the length
of the side
of a triangle, then we can only use the positive value.
The distance from the ramp’s contact point with the ground and
the base
of the platform is 4 feet.
Need more help on these topics? Formulas
for Two-Dimensional Figures
|
11 - 4.
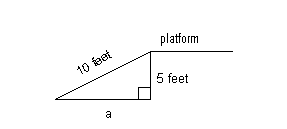
A ramp 10 feet long is leaning against a raised platform which
is 5
feet above the ground. What is the distance from the ramp’s contact
point
with the ground and the base of the platform?
|
 Answer:
C Answer:
C
Anytime you are missing one side of a right triangle, you can
use the Pythagorean
theorem to find that long lost side:

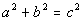
The variables in this formula represent the following:
a and b
= legs
of the right triangle
c = hypotenuse of the right
triangle
In this problem,
a = ? = this is the variable we are
looking
for
b = 5
c = 10
Plugging these values into the formula and solving for a
we get:
|
|
*Plug in 5 for b
and 10 for c
*Inv. of add 25 is sub. 25
*Square root method
|
Since a represents the length
of the side
of a triangle, then we can only use the positive value.
The distance from the ramp’s contact point with the ground and
the base
of the platform is 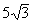 feet.
feet.
Need more help on these topics? Formulas
for Two-Dimensional Figures
|
11 - 5.
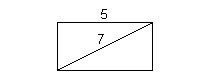
What is the area of the rectangle above?
|
 Answer:
A Answer:
A
The area of a rectangle is length times width. So, we
need the
length and the width to get our answer.
It looks like we have the length which is 5, but we still need
the width.
Note how we have the diagonal of the rectangle, which is
7. The
diagonal, length and width of the rectangle make up an right
triangle.
Anytime you are missing one side of a right triangle, you can
use the Pythagorean
theorem to find that long lost side:

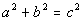
The variables in this formula represent the following:
a and b
= legs
of the right triangle
c = hypotenuse of the right
triangle
In this problem,
a = ? = this is the variable we are
looking
for
b = 5
c = 7
Plugging these values into the formula and solving for a
we get:
|
|
*Plug in 5 for b
and 7 for c
*Inv. of add 25 is sub. 25
*Square root method |
2 square root of 6 is the width of the rectangle.
Putting the length and the width values of the rectangle
into the
area formula we get:
|
|
*Plug in 5 for length and 2 square root
of
6 for width
|
12 - 1.
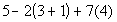 = =
|
 Answer:
E Answer:
E
Using the order of operations we get:
|
|
*( )
*Multiplication
*Add and subtract
|
12 - 2.
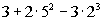 = =
|
 Answer:
B Answer:
B
Using the order of operations we get:
|
|
*exponents
*Multiplication
*Add and subtract
|
12 - 3.
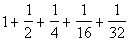 = =
|
 Answer:
D Answer:
D
Adding the fractions we get:
|
|
*Writing equivalent fractions with LCD
of
32
*Add |
12 - 4.
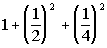 =
=
|
 Answer:
E Answer:
E
Using the order of operations we get:
|
|
*exponents
*Writing equivalent fractions with
LCD of 16
*Add
|
12 - 5.
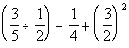 =
=
|
 Answer:
B Answer:
B
Using the order of operations we get:
|
|
*Exponents
*Rewrite division as mult. of the
reciprocal
*Writing equivalent fractions with
LCD of 20
*Add
|
13 - 1.
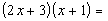
|
 Answer:
C Answer:
C
Using the FOIL method we get:
|
|
*First Outside Inside Last
*Add like terms |
13 - 2.
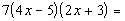
|
 Answer:
E Answer:
E
Using the FOIL method and distributive property we get:
|
|
*First Outside Inside Last
*Distribute the 7
*Add like terms |
13 - 3.
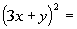
|
 Answer:
C Answer:
C
Squaring the binomial we get:
|
|
*Square the binomial
*First Outside Inside Last
*Add like terms |
13 - 4.
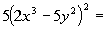
|
 Answer:
A Answer:
A
Squaring the binomial and then using distributive property
we get:
|
|
*Square the binomial
*First Outside Inside Last
*Distribute the 5
*Add like terms |
13 - 5.
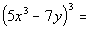
|
 Answer:
A Answer:
A
Cubing the binomial we get:
|
|
*Cube the binomial
*Multiply last two binomials
*Add like terms
|
14 - 1. A student got 80% of 40 questions
correct.
How many questions did he get correct? |
 Answer:
E Answer:
E
When you take a percent of a number you multiply the decimal
form of
that percent times the number.
Finding 80% of 40:
|
|
*Move decimal two to the left to write
80%
as .8
*Multiply
|
He got 32 questions correct.
Need more help on these topics? Decimals
and Percents
|
14 - 2. Quiz scores on a history exam are
9, 9,
7, 10, and 5. If there is one more quiz, what would need to be
made
on that quiz to have an overall average of 7? |
 Answer:
A Answer:
A
In this problem we are given the mean and we need to find one
of our
values.
Keep in mind that this is still a mean problem. We will
still
use the idea that we need to sum up the exams and then divide it by 6
to
get the mean. We can let our unknown exam be x.
Using the mean formula we get:
|
|
*(sum of tests)/(# of tests) = mean
*Solve for x (missing
quiz)
*Mult. both sides by LCD of 6
*Inverse of add 40 is sub. 40
|
A score of 2 would be needed to have an overall average of
7.
Need more help on these topics? Averages
(Mean)
|
14 - 3. A student has quiz scores of 70,
75 and
55. If tests count as 2 quiz grades, what would he have to make
on
a test, so that the overall average is 70? |
 Answer:
D Answer:
D
In this problem we are given the mean and we need to find one
of our
values.
Keep in mind that this is still a mean problem. We will
still
use the idea that we need to sum up the exams and then divide it by 5
to
get the mean. We can let our unknown exam be x.
Keep in mind that a test score counts twice.
Using the mean formula we get:
|
|
*(sum of tests)/(# of tests) = mean
*Need 2 x's
since
tests count twice
*Solve for x (missing
test)
*Mult. both sides by LCD of 5
*Inverse of add 200 is sub. 200
*Inverse of mult. by 2 is divide by 2
|
The test score would have to be at least 75.
Need more help on these topics? Averages
(Mean)
|
14 - 4. If 30 students in one class had
an average
of 80% and 10 students from another class had another average of 90%,
what
is the average in % of all 40 students? |
 Answer:
C Answer:
C
In general, when finding the average of tests, you add the
tests together
and then divide by the number of tests.
On this problem we have two separate averages to start with.
So we need
to find the total number of points we have using that information
and then divide by the number of students, which, in this case, is 40.
If 30 students averaged 80, then the total number of points
would be
(30)(80) = 2400.
If 10 students averaged 90, then the total number of points
would be
(10)(90) = 900.
So the total number of points is 2400 + 900 = 3300.
To find the average, take the number of points and divide
by the
number of students:
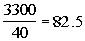
The overall average percent is 82.5%.
Need more help on these topics? Averages
(Mean)
|
14 - 5. If 5 students in one class had an
average
of 55%, 15 students in one class had an average of 80% and 7 students
from
another class had another average of 92%, approximately, what is the
average
in % of all 27 students? |
 Answer:
A Answer:
A
In general, when finding the average of tests, you add the
tests together
and then divide by the number of tests.
On this problem we have three separate averages to start with.
So we
need to find the total number of points we have using that
information
and then divide by the number of students, which in this case, is 27.
If 5 students averaged 55, then the total number of points
would be
(5)(55) = 275.
If 15 students averaged 80, then the total number of points
would be
(15)(80) = 1200.
If 7 students averaged 92, then the total number of points
would be
(7)(92) = 644.
So the total number of points is 275 + 1200 + 644 = 2119.
To find the average, take the number of points and divide
by the
number of students:
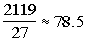
The overall average percent is 78.5%.
Need more help on these topics? Averages
(Mean)
|
15 - 1. 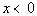 and 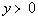 |
Column A
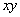 |
Column B
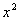 |
 Answer:
B Answer:
B
Since x is less than 0, then it
is a negative
number.
Since y is greater than 0, then
it is a
positive number.
With that in mind, when you multiply x
times y,
you will have a negative times a positive. That means the
product xy
will be negative.
When you square x, you will
end up with
a positive value.
Since ALL positive numbers are greater than ALL negative
numbers, 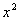 will be greater than
will be greater than 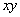 . .
Need more help on these topics? Exponents
and Linear
Inequality
|
15 - 2. 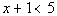 and 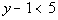 |
 Answer:
D Answer:
D
Solving the first inequality for x
we
get:
|
Solving the second inequality for y
we get: |
Even though 6 is greater than 4, we cannot determine the
relationship
because x can be ANY number less than 4
and y can be ANY number less than 6. So y
could
be 2 and x could be 3 OR y
could be 2 and x could be -5, etc...
Need more help on these topics? Linear
Inequality
|
15 - 3. 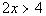 and 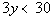 |
 Answer:
D Answer:
D
Solving the first inequality for x
we
get:
|
|
*Inv. of mult. by 2 is div. by 2 |
Solving the second inequality for y
we get: |
|
*Inv. of mult. by 3 is div. by 3 |
We cannot determine the relationship because x
can be ANY number greater than 2 and y can
be ANY number less than 10. So y
could
be 2 and x could be 3 OR y
could be 5 and x could be 3, etc....
Need more help on these topics? Linear
Inequality
|
15 - 4. 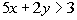 |
Column A
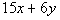 |
Column B
9 |
 Answer:
A Answer:
A
Note how 15x + 6y
is three times 5x + 2y.
Taking 3 times the given inequality we get:
|
|
*Multiply BOTH sides by 3 |
15 - 5. 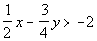 |
Column A
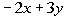 |
Column B
8 |
 Answer:
B Answer:
B
Note how -2x + 3y
is a negative four times 1/2x - 3/4y.
Taking -4 times the given inequality we get:
|
|
*Multiply BOTH sides by -4
*Since we are mult. both sides by a
negative
number
we need to change the inequality
sign |
16 - 1.
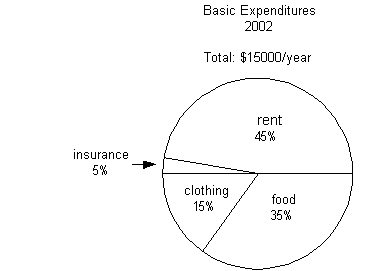
How much was spent on rent in 2002?
|
 Answer:
B Answer:
B
Since 45% of the basic expenditures was spent on rent, then we
will
need to take 45% of $15000 to find the answer to this question.
Whenever you take a percent of a number you take the decimal
form of
that percent times the number:
|
|
*Move decimal on 45% two places to the
left
|
16 - 2.

What was the total amount spent on food and clothing in 2002?
|
 Answer:
B Answer:
B
Together food and clothing is 35% + 15% = 50% of the basic
expenditures.
Since 50% of the basic expenditures was spent on food and
clothing,
then we will need to take 50% of $15000 to find the answer to this
question.
Whenever you take a percent of a number you take the decimal
form of
that percent times the number:
|
|
*Move decimal on 50% two places to the
left
|
16 - 3.

How much more money was spent on clothing than insurance in
2002?
|
 Answer:
A Answer:
A
We need to find the difference between what was spent on
clothing versus
insurance.
There was 15% - 5% = 10% more spent on clothing than
insurance.
Since 10% more of the basic expenditures was spent on clothing
than
on insurance, then we will need to take 10% of $15000 to find the
answer
to this question.
Whenever you take a percent of a number you take the decimal
form of
that percent times the number:
|
|
*Move decimal on 10% two places to the
left
|
16 - 4.

How much more was spent on rent and insurance than on food in
2002?
|
 Answer:
E Answer:
E
Together, rent and insurance is 45% + 5% = 50% of the basic
expenditures
We need to find the difference between what was spent on rent
and insurance
versus food. There was 50% - 35% = 15% more spent on rent and
insurance
than food.
Since 15% more of the basic expenditures was spent on rent and
insurance
than on food, then we will need to take 15% of $15000 to find the
answer
to this question.
Whenever you take a percent of a number you take the decimal
form of
that percent times the number:
|
|
*Move decimal on 15% two places to the
left
|
16 - 5.

If the amount that was spent on food is 5% higher in 2002 than
2001,
approximately what amount was spent on food in 2001?
|
 Answer:
B Answer:
B
We need to be careful here, the temptation is to just take 40%
- 5%
= 35% of 15000. However, keep in mind that we are talking
about
5% higher in terms of amount, not compared to the other
expenditures
and the total amount may or may not have been the same overall
for
2001.
The first thing we need to find is the actual amount spent on
food in
2002. According to the chart, food made up 35% of the 15,000
spent.
Taking 35% of 15,000 we get:
|
|
*Move decimal on 35% two places to the
left
|
5250 is 5% higher than what was spent on food in
2001.
Letting x represent the 2001
amount spent
on food and putting this into an equation we get:
|
|
*5% higher means we ADD 5% (or .05)
of the
amount
*Divide BOTH sides by 1.05
|
17 - 1.
 |
Column A
The ratio of food to clothing. |
Column B
The ratio of clothing to food. |
 Answer:
A Answer:
A
You can do this problem two different ways. You can
either take
the ratio of the percents for each expenditure or you can find the
amount
that go with each one and take that ratio. Either way you would
end
up with the same answer.
I’m going to use the percents that are given to set up each
ratio.
For the ratio of food to clothing, we need to make
sure that
the percent attached to food goes on top and the percent for clothing
goes
on bottom:
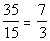
For the ratio of clothing to food, we need to make
sure that
the percent attached to clothing goes on top and the percent for food
goes
on bottom:
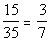
It looks like the ratio of food to clothing is greater
than the ratio
of clothing to food.
Need more help on these topics? Percent
and Problem Solving
|
17 - 2.
 |
Column A
The ratio of food to rent. |
Column B
The ratio of rent to food. |
 Answer:
B Answer:
B
You can do this problem two different ways. You can
either take
the ratio of the percents for each expenditure or you can find the
amount
that go with each one and take that ratio. Either way you would
end
up with the same answer.
I’m going to use the percents that are given to set up each
ratio.
For the ratio of food to rent, we need to make sure
that the
percent attached to food goes on top and the percent for rent goes on
bottom:
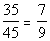
For the ratio of rent to food, we need to make sure
that the
percent attached to rent goes on top and the percent for food goes on
bottom:
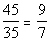
It looks like the ratio of rent to food is greater than the
ratio
of food to rent.
Need more help on these topics? Percent
and Problem Solving
|
17 - 3.
 |
Column A
The ratio of food to insurance. |
Column B
The ratio of insurance to food. |
 Answer:
A Answer:
A
You can do this problem two different ways. You can
either take
the ratio of the percents for each expenditure or you can find the
amount
that go with each one and take that ratio. Either way you would
end
up with the same answer.
I’m going to use the percents that are given to set up each
ratio.
For the ratio of food to insurance, we need to make
sure that
the percent attached to food goes on top and the percent for insurance
goes on bottom:
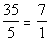
For the ratio of insurance to food, we need to make
sure that
the percent attached to insurance goes on top and the percent for food
goes on bottom:
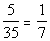
It looks like the ratio of food to insurance is greater
than the
ratio of insurance to food.
Need more help on these topics? Percent
and Problem Solving
|
17 - 4.
 |
Column A
The ratio of insurance and rent to food and clothing. |
Column B
The ratio of food and clothing to insurance and rent. |
 Answer:
C Answer:
C
The total percent for insurance and rent is 5% + 45% = 50%.
The total percent for food and clothing is 35% + 15% = 50%.
You can do this problem two different ways. You can
either take
the ratio of the percents for each expenditure or you can find the
amount
that go with each one and take that ratio. Either way you would
end
up with the same answer.
I’m going to use the percents that are given to set up each
ratio.
For the ratio of insurance and rent to food and clothing,
we
need to make sure that the percent attached to insurance and rent goes
on top and the percent for food and clothing goes on bottom:
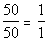
For the ratio of food and clothing to insurance and
rent,
we need to make sure that the percent attached to food and clothing
goes
on top and the percent for insurance and rent goes on bottom:
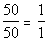
It looks like the two ratios are the same.
Need more help on these topics? Percent
and Problem Solving
|
17 - 5.
 |
Column A
The ratio of food and insurance
to clothing and rent. |
Column B
The ratio to clothing and rent
to food an insurance. |
 Answer:
B Answer:
B
The total percent for food and insurance is 35% + 5% = 40%.
The total percent for clothing and rent is 15% + 45% = 60%.
You can do this problem two different ways. You can
either take
the ratio of the percents for each expenditure or you can find the
amount
that go with each one and take that ratio. Either way you would
end
up with the same answer.
I’m going to use the percents that are given to set up each
ratio.
For the ratio of food and insurance to clothing and rent,
we
need to make sure that the percent attached to food and insurance goes
on top and the percent for clothing and rent goes on bottom:
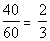
For the ratio of clothing and rent to food and insurance,
we
need to make sure that the percent attached to clothing and rent goes
on
top and the percent for food and insurance goes on bottom:
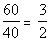
The ratio of clothing and rent to food and insurance is
greater than
the ratio of food and insurance to clothing and rent.
Need more help on these topics? Percent
and Problem Solving
|
18 - 1.
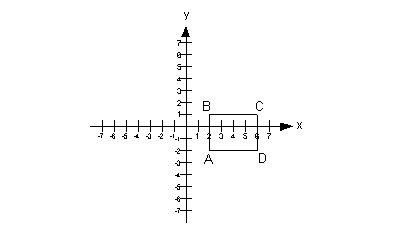
Find the area of rectangle ABCD shown above.
|
 Answer:
E Answer:
E
The area of a rectangle is length times width.
Side BC can be found by taking the absolute value of the
difference
of the x values of their ordered pairs,
which
would be is |6 - 2| = 4.
Side BA can be found by taking the absolute value of the
difference
of the y values of their ordered pairs,
which
would be |1 - (-2)| = 3.
Putting these values into the area formula for a rectangle
we get:
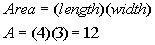
The area of the rectangle is 12.
Need more help on these topics? Formulas
for Two-Dimensional Figures and Coordinate
Geometry
|
18 - 2.
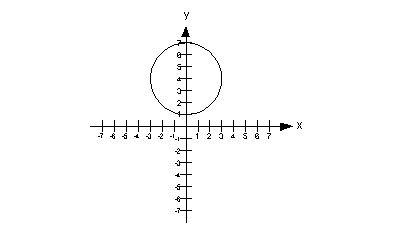
Find the area of the circle shown above.
|
 Answer:
B Answer:
B
The area of a circle is 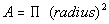 . .
Note how the circle’s widest part goes from (3, 4) to (-3,
4).
This means that the diameter spans 6 units. If the radius is half
of the diameter, that means the radius is 3.
Putting 3 in for the radius in the area of a circle formula
we get:
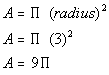
The area of the circle is 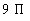 . .
Need more help on these topics? Formulas
for Two-Dimensional Figures and Coordinate
Geometry
|
18 - 3.
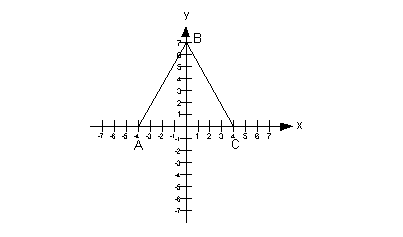
Find the area of triangle ABC shown above.
|
 Answer:
B Answer:
B
The area of a triangle is 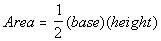 . .
The base, side AC, can be found by taking the absolute value
of the
difference of the x values of their
ordered
pairs, which would be is |4 - (-4)| = 8.
The height can be found by taking the absolute value of the
difference
of the y values of B and the origin,
which
would be |7 - 0| = 7.
Putting in 8 for the base and 7 for the height into the
area of a
triangle formula we get:
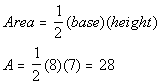
The area of the triangle is 28.
Need more help on these topics? Formulas
for Two-Dimensional Figures and Coordinate
Geometry
|
18 - 4.
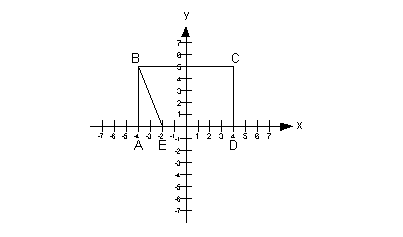
Find the area enclosed by BCDE shown above.
|
 Answer:
D Answer:
D
From the picture, we can see that figure BCDE is a
quadrilateral but
it doesn’t fit into a form like rectangle, parallelogram, etc...
We will have to take the area of rectangle ABCD and subtract from it
the
area of triangle ABE, this will leave us with the area of figure
BCDE.
Lets look at rectangle ABCD first. The area of a
rectangle is
length times width.
Side AB can be found by taking the absolute value of the
difference
of the y values of their ordered pairs,
which
would be |5 - 0| = 5.
Side BC can be found by taking the absolute value of the
difference
of the x values of their ordered pairs,
which
would be |4 - (- 4)| = 8.
Plugging 8 in for the length and 5 in for the width into
the formula
for the area of a rectangle we get:
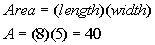
The area of rectangle ABCD is 40.
Now lets look at triangle ABE. The area of a triangle
is 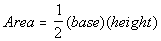 . .
So we need to know the base and the height of this
triangle. The
base of this triangle is side AE. The height of this triangle is
side AB.
Side AE can be found by taking the absolute value of the
difference
of the x values of their ordered pairs,
which
would be |-2 - (-4)| = 2.
Side AB can be found by taking the absolute value of the
difference
of the y values of their ordered pairs, which would be |5 - 0| = 5.
Plugging 2 in for the base and 5 in for the height into the
formula
for the area of a triangle we get:
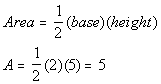
The area of triangle ABE is 5.
Last, we need to take the difference of the area of the
rectangle
and triangle:
40 - 5 = 35
The area of the figure BCDE is 35.
Need more help on these topics? Formulas
for Two-Dimensional Figures and Coordinate
Geometry
|
18 - 5.
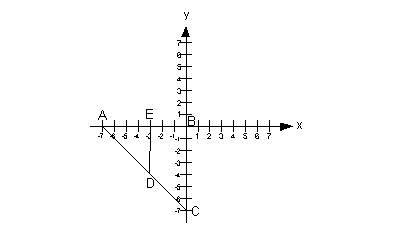
Find the area enclosed by BCDE shown above.
|
 Answer:
C Answer:
C
From the picture, we can see that figure BCDE is a
quadrilateral but
it doesn’t fit into a form like rectangle, parallelogram, etc...
We will have to take the area of triangle ABC and subtract from it the
area of triangle AED, this will leave us with the area of figure
BCDE.
Let's look at triangle ABC first. The area of a triangle
is 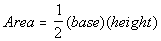 . .
So we need to know the base and the height of this
triangle. Since
it is a right triangle, the base and height are going to be the lengths
of the two legs, which are sides AB and BC.
Side BC can be found by taking the absolute value of the
difference
of the y values of their ordered pairs,
which
would be |-7 - 0| = 7.
Side AB can be found by taking the absolute value of the
difference
of the x values of their ordered pairs, which would be |-7 - 0| = 7.
Plugging 7 in for the base and 7 in for the height into the
formula
for the area of a triangle we get:
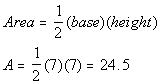
The area of triangle ABC is 24.5.
Now let's look at triangle AED. So we need to know
the base
and the height of this triangle.
The base of this triangle is side AE. The height of this
triangle
is
side DE.
Side AE can be found by taking the absolute value of the
difference
of the x values of their ordered pairs,
which
would be |-7 - (-3)| = 4.
Side DE can be found by taking the absolute value of the
difference
of the y values of their ordered pairs,
which
would be |0 - (-4)| = 4.
Plugging 4 in for the base and 4 in for the height into the
formula
for the area of a triangle we get:
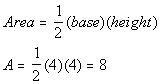
The area of triangle AED is 8.
Last, we need to take the difference of the areas of the
two triangles:
24.5 - 8 = 16.5
The area of the figure BCDE is 16.5.
Need more help on these topics? Formulas
for Two-Dimensional Figures and Coordinate
Geometry
|
19 - 1. What is the solution(s) to 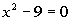
? |
 Answer:
B Answer:
B |
|
*Factor the difference of squares
*Set 1st factor = 0
*Set 2nd factor = 0
|
19 - 2. What is the solution(s) to 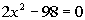
? |
 Answer:
D Answer:
D |
|
*Factor out the GCF of 2
*Factor the difference of squares
*Set 1st factor = 0
*Set 2nd factor = 0
|
19 - 3. What is the solution(s) to 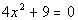
? |
 Answer:
E Answer:
E |
|
*Solve for x
*Square root method
*Square root of -1 is i
|
19 - 4. What is the solution(s) to 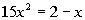
? |
 Answer:
C Answer:
C |
|
*Factor the trinomial
*Set the 1st factor = 0
*Inv. of add 2 is sub. 2
*Inv. of mult. by 5 is div. by 5
*Set the 2nd factor = 0
*Inv. of sub. 1 is add 1
*Inv. of mult. by 3 is div. by 3
|
19 - 5. What is the solution(s) to 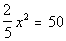
? |
 Answer:
B Answer:
B |
|
*Inv. of mult. by 2/5 is mult. by 5/2
*Square root method
|

WTAMU > Virtual Math Lab > GRE Math
Disclaimer:
Note that we can not
guarantee that you will pass your test after going through any of the tutorials
in this website. However, it will definitely help you to better
understand the topics covered. WTAMU and Kim Seward are not responsible
for how a student does on any test for any reason including not being able
to access the website due to any technology problems.
GRE and Graduate Record Examination are the
registered trademarks of Educational Testing Service (ETS). The material here has
neither been reviewed nor endorsed by ETS.
Throughout this website, we link to various
outside sources.
WTAMU and Kim Seward do not have any ownership to any of these outside
websites and cannot give you permission to make any kind of copies of
anything found at any of these websites that we link to. It is purely for
you to link to for information or fun as you go through the study
session. Each of these websites have a copy right clause that you need to read
carefully if you are wanting to do anything other than go to the website and read
it. We discourage any illegal use of the webpages found at these
sites.
|
All contents copyright (C) 2003 - 2008, WTAMU and Kim Seward. All rights reserved.
Last revised on December 22, 2008 by Kim Seward.
|
|
|


