GRE Math Practice Test II
Answer Key with Explanations
P. 1 (Problems 1 - 9)
WTAMU > Virtual Math Lab > GRE Math
| Because of the enormity of this
part, I split the answer/discussion into three pages. This page, P. 1,
has the answer/explanations to all levels of the first 9 problems. P.
2 has the answer/explanations to all levels of problems 10 -
19. P.
3 has the answer/explanations to all levels of problems 20 -
28.
This page also has links to the mathematical area(s) that each
question comes from in case you need to go back and review.
Printing
warning:
Note that because of all of the levels per problem, there are a lot of
questions on this page. So if you wish to print this out, note
that there
will be a lot of pages to print. |
Column A
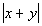 |
Column B
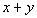 |
 Answer: D Answer: D
If x and y
are integers, that means they can be negative, positive or zero.
Since Column A has an absolute value around x
+ y,
that means its value will always be nonnegative. Now, Column B
does not have an absolute value around x + y.
Its value can be negative, positive or zero. When Column B comes
out nonnegative, then it will be equal to Column A. However, if
Column B’s value is negative then, Column A’s value is going to be
greater.
For example if x = 1 and y
= 2, then both columns will have a value of 3. But if x
= 5 and y = -10, then Column A will be 5
and Column B will be -5.
Since we don’t know which it will be, the relationship cannot
be determined from the information given.
Need more help on this topic? Absolute Value
|
Column A
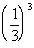 |
Column B
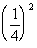 |
 Answer: B Answer: B
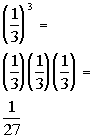
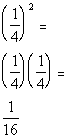
Since 1/16 is greater than 1/27, Column B's value is
greater than Column A's value.
Need more help on this topic? Fractions
and Exponents
|
Column A
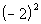 |
Column B
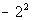 |
 Answer:
A Answer:
A
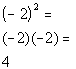
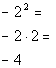
Hey, they look a lot alike, but they are not exactly the same.
Can you see the difference between the two?? Hopefully, you noticed that in
Column A, there was a ( ) around the - and the 2. In Column B, there is no (
). This means the - is NOT part of the base, so it will not get expanded
like it did in Column A. It is interpreted as finding the negative or
opposite of 2 squared.
Hence, Column A's value is greater than Column B's value.
Need more help on this topic? Exponents
|
3 - 1. A cylindrical building contains
wheat. The building has a radius of 20 feet and a depth of 50 feet. What is
the volume of this cylindrical building? |
 Answer: D Answer: D
We need to know the formula for the volume of a
cylindrical building:
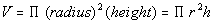
Filling in 20 for radius and 50 for height we get:
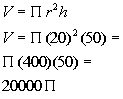
The volume of the building is 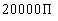 cubic feet.
cubic feet.
Need more help on this topic? Formulas for Three-Dimensional Figures
|
3 - 3. A cylindrical building contains
wheat. The building has a diameter of 17 feet and a depth of 40 feet. What
is the volume of this cylindrical building? |
 Answer: B Answer: B
We need to know the formula for the volume of a
cylindrical building:
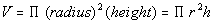
Note how the problem gave us the DIAMETER. To find the
radius we need to divide the diameter of 17 by 2. This will give us
8.5 for our radius.
Filling in 8.5 for radius and 40 for height we get:
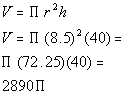
The volume of the building is 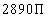 cubic feet.
cubic feet.
Need more help on this topic? Formulas
for Three-Dimensional Figures
|
3 - 5. Two identical cylindrical buildings
contain wheat.
Each building has a diameter of 21 feet and a depth of 30 feet.
If one cubic foot of wheat weighs 7 pounds, approximately how many pounds
of wheat can be stored if both building are full. |
 Answer: E Answer: E
First, let’s find the volume of each cylindrical
building. The volume of a cylindrical building is
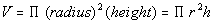
Note how the problem gave us the DIAMETER. To find the
radius we need to divide the diameter of 21 by 2. This will give us
10.5 for our radius.
Filling in 10.5 for radius and 30 for height we get:
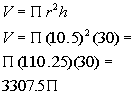
Next we want to consider the fact that we have two buildings. Multiplying
the volume by two we get:
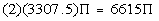
Next we want to consider that there are about 7 pounds of
wheat per cubic foot. Multiplying the volume of the two cylinders by 7
we get:
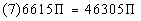
Next notice that none of the answers has the pi symbol in
them. That means we will have to put in 3.14 for pi
and see what we get:
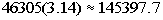
About 145,398 pounds of wheat could be stored in these two
buildings.
Need more help on this topic? Formulas for Three-Dimensional Figures
|
Column A
30% of 50,000 |
Column B
1500 |
 Answer: A Answer: A
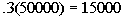
|
*Move decimal on 30% two places to
the left |
Since 15000 > 1500, the answer is Column A’s quantity
is greater.
Need more help on these topics? Decimals
and Percents
|
Column A
7% of 25,000 |
Column B
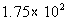 |
 Answer: A Answer: A
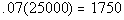
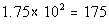
|
*Move decimal on 7% two places to
the left
*Move decimal two places to the RIGHT |
Column A
7.5% of 8000 |
Column B
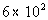 |
 Answer:
C Answer:
C
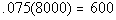
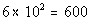
|
*Move decimal on 7.5% two places to
the left
*Move decimal two places to the RIGHT |
Column A
.065% of .4 |
Column B
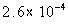 |
 Answer: C Answer: C
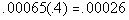
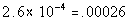
|
*Move decimal on .065% two places to
the left
*Move decimal four places to the LEFT |
5 - 1. If 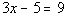 ,
what is the value of x? |
 Answer:
C Answer:
C
Solving the equation for x
we get:
|
|
*Inverse of sub. 5 is add 5 to BOTH
sides
*Inverse of mult. by 3 is divide by 3
|
5 - 2. If 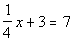 ,
what is the value of x? |
 Answer:
D Answer:
D
Solving the equation for x
we get:
|
|
*Mult. BOTH sides by the LCD of 4
*Inverse of add 12 is sub. 12 from
BOTH sides
|
5 - 3. If 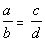 ,
and a, b,
c,
and d are positive integers, then which
of
the following must be true? |
 Answer:
E Answer:
E
Doing a cross multiplication we get:
|
5 - 4. If 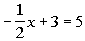 ,
what is the value of 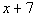 ? |
|
*Mult. BOTH sides by the LCD of -2
*Inverse of sub. 6 is add 6 to BOTH
sides
|
Now be careful, this is not our final answer.
We still need to plug in -4 for x
in
the given expression:
|
5 - 5. If 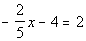 ,
what is the value of 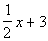 ? |
 Answer:
A Answer:
A
The first step here is to find the value of x.
If we know that, then we can plug that in to the second expression and
find out what 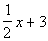 is.
is.
Solving the equation for x
we get:
|
|
*Mult. BOTH sides by the LCD of -5
*Inverse of add 20 is sub. 20 to BOTH
sides
*Inverse of mult. by 2 is divide by 2
|
Now be careful, this is not our final answer.
We still need to plug in -15 for x
in
the given expression:
|
Column A
Two different coins are tossed.
The number of possible outcomes
of tossing the two coins. |
Column B
4 |
 Answer:
C Answer:
C
We can use the fundamental counting principle to answer this
question.
Basically we need to take the product of the number of ways each event
can occur.
There are 2 stages or events: coin 1 and coin 2
There are two possibilities for each coin, heads or
tails.
Putting that all together we get:
|
|
Coin 1
|
|
Coin 2
|
|
Total
|
|
2
|
x
|
2
|
=
|
4
|
Since there are 4 different possible tosses of two coins,
the two
quantities are the same.
Need more help on this topic? Counting
Principle
|
Column A
A combo special includes one sandwich,
one bag of chips and one drink.
There are four types of sandwiches,
three types of chips and three types of drinks.
The number of combos possible. |
Column B
24
|
 Answer:
A Answer:
A
We can use the fundamental counting principle to answer this
question.
Basically we need to take the product of the number of ways each event
can occur.
There are 3 stages or events: choosing a sandwich, chips, and
a drink.
There are four types of sandwiches, three types of chips and
three types
of drinks.
Putting that all together we get:
|
|
Sandwich
|
|
Chips
|
|
Drinks
|
|
Total
|
|
4
|
x
|
3
|
x
|
3
|
=
|
36
|
Since 36 is larger than 24, the number of different
possible combos
is a larger value than 24.
Need more help on this topic? Counting
Principle
|
Column A
The number of ways to arrange
five CD’s on a shelf. |
Column B
125 |
 Answer:
B Answer:
B
Since we are counting how many ways to ARRANGE the CD’s, this
is a permutation
problem. The permutation of n
things
taken r at a time is
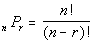
Putting a 5 in for r and for
n
we get:
|
|
*Permutation formula
*Plugging 5 for n
and r
*0! = 1
|
Since 125 is larger than 120, 125 is a larger value than
the number
of different possible arrangements of five CD's.
Need more help on this topic? Permutations
|
Column A
Probability of randomly selecting a
given name out of a hat containing
fifteen different names. |
Column B
.07 |
 Answer:
B Answer:
B
In Column A, each name has an equally likely chance of being
picked.
The probability of randomly selecting a given name out of a
hat containing
15 different names can be found by taking the number of names being
selected,
which in this case is 1, and put that over the total number of names,
which
is 15:
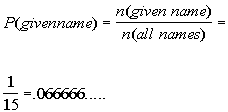
Since .07 is larger than .066666...., .07 is a larger
value
than the probability of randomly selecting a given name out if a hat
containing
15 different names.
Need more help on this topic? Probability
|
Column A
A bag contains four red, twelve green,
and 14 black jelly beans.
The probability that a red one is not picked. |
Column B
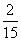 |
 Answer:
A Answer:
A
In Column A, each jelly bean has an equally likely chance of
being picked.
The probability of randomly selecting a jelly bean that is not
red can
be found by taking the number of jelly beans that are not red, which in
this case is 26, and put that over the total number of jelly
beans,
which is 30:
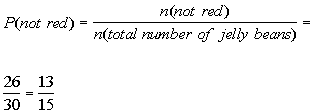
Since 13/15 is larger than 2/15, the probability of
randomly selecting
a jelly bean that is not red is larger than 2/15.
Need more help on this topic? Probability
|
7 - 1. 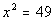 |
 Answer:
D Answer:
D
Solving the given equation for x
we get:
|
|
*Factor the Difference of Squares
*Set 1st factor = 0
*Set 2nd factor = 0 |
Since x can be either 7 OR
-7, the relationship
cannot be determined from the information given.
Need more help on these topics? Solving
Quadratic Equations
|
7 - 2. 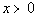 |
Column A
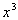 |
Column B
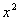 |
 Answer:
D Answer:
D
Since x
can be ANY
value greater than 0, that means it could be a fractional number
between 0 and 1, or a number greater than or equal to 1.
If x is ½, then
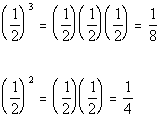
In this case Column B’s value is greater.
But let’s look at an example where x
is greater than 1.
Let's try 2:
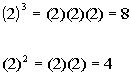
This time Column A’s value is greater.
If x was 1, the two values
would be the same.
Hence, the relationship cannot be determined from the
information given.
Need more help on these topics? Exponents
|
7 - 3. 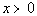 |
Column A
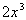 |
Column B
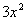 |
 Answer:
D Answer:
D
Since x
can be ANY
value greater than 0, that means it could be a fractional number
between
0 and 1, or a number greater than or equal to 1.
If x
is ½,
then
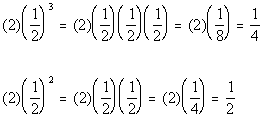
In this case Column B’s value is greater.
But let’s look at an example where x
is greater than 1.
Lets try 2:
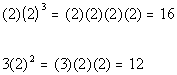
This time Column A’s value is greater.
Hence, the relationship cannot be determined from the
information given.
Need more help on these topics? Exponents
|
7 - 4. x is a
positive integer: 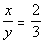 |
 Answer:
A Answer:
A
If we did a cross multiplication and solve for y
we would get:
|
|
*Cross multiply
*Inv. of mult. by 2 is divide by 2
|
It is given that x is a
positive integer.
That could mean x is 1, 2, 3, ....
If x is 1, then y
would equal 3/2. If x is an
integer greater
than or equal to 2 then y would be
greater
than 3/2, which means y will always be
greater
than 1.
y has a larger value than 1.
Need more help on these topics? Solving
Linear Equations
|
7 - 5. 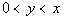 |
Column A
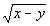 |
Column B
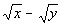 |
 Answer:
A Answer:
A
The temptation here is to say that the two values are equal to
each other. However, if you put in any value such that 0 < y
< x, you will find that Column A’s
value is greater than Column B’s value.
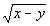 is a
larger value than is a
larger value than 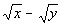 . .
Need more help on these topics? Square Root
|
8 - 1.
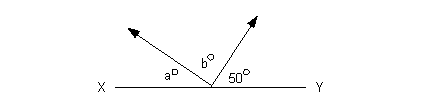
In the figure above, if XY is a line segment, what is the
number of degrees in the sum of a + b?
a and b
are measured in degrees.
|
 Answer:
D Answer:
D
Since XY is a line segment, that means its angle measurement
is 180 degrees, which in turn means that
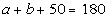
Subtracting 50 from both sides will give us the sum of a and
b:
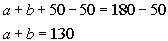
The sum of the angles a and b
is 130 degrees.
Need more help on these topics? Basic Geometry
|
8 - 2.
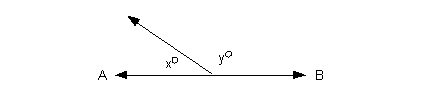
In the figure above, if AB is a straight line and 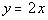 ,
then how many degrees is y? ,
then how many degrees is y?
x and y
are
measured in degrees.
|
 Answer:
C Answer:
C
Since AB is a straight line, its angle measurement is 180
degrees. This means that 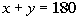 . .
We can use this to find our missing value. Substituting
in 2x
for y we get:
|
|
*The sum of the angles is 180
*Substitute in 2x
for y
*Inv. of mult. by 3 is divide by 3
|
If x is 60 degrees and y
= 2x, then |
8 - 3.
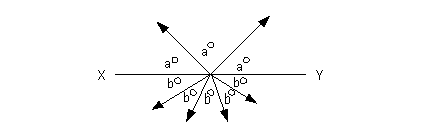
In the figure above, if XY is a line segment, how many degrees
is 4a?
a and b
are measured in degrees.
|
 Answer:
D Answer:
D
Since 3 angles of measure a
make up XY
and XY is a line segment, that means
the 3 a angles would have to make up 180
degrees.
|
|
*The 3 a
angles
= 180 degrees
*Divide BOTH sides by 3
|
Now that we know what a is
equal to, all
we have to do is multiply that by 4 and get our answer:
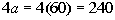 |
4a is equal to 240 degrees.
Need more help on these topics? Basic
Geometry
|
8 - 4.

In the figure above, if XY is a line segment, what is the value of 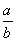 ?
a and b
are measured in degrees.
|
 Answer:
B Answer:
B
Since 3 angles of measure a
make up XY
and XY is a line segment, that
means the 4 a angles would have to make up 180
degrees.
Similarly, the 5 b angles would
be 180 degrees.
This would give us enough information to find out what aand b are equal to.
Lets start with a:
|
|
*The 3 a
angles = 180 degrees
*Divide BOTH sides by 3
|
|
*The 5 b
angles
= 180 degrees
*Divide BOTH sides by 5
|
Putting those values in for a
and bwe get: |
|
*Plug in 60 for a
and 36 for b |
8 - 5.

In the figure above, if XY is a line segment, what is the
value of 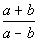 ? ?
a and b
are measured in degrees.
|
 Answer: D Answer: D
Since 3 angles of measure a
make up XY
and XY is a line segment, that
means the 4 a angles would have to make up 180
degrees.
Similarly, the 5 b angles would
be 180 degrees.
This would give us enough information to find out what a and b are equal to.
Let's start with a:
|
|
*The 3 a
angles = 180 degrees
*Divide BOTH sides by 3
|
|
*The 5 b
angles = 180 degrees
*Divide BOTH sides by 5
|
Putting those values in for a
and b we get: |
|
*Plug in 60 for a
and 36 for b
|
Column A
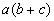 |
Column B
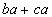 |
 Answer: C Answer: C
Using the distributive for Column A we get:
|
|
*distributive property
*commutative property |
Column A
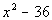 |
Column B
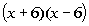 |
 Answer:
C Answer:
C
Factoring Column A we get:
|
|
*Factor the difference of two squares
|
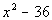 is
the same as 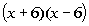 .
Need more help on these topics? Factoring
|
Column A
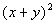 |
Column B
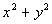 |
 Answer:
D Answer:
D
Squaring Column A we get:
|
It is real tempting to say that Column A is greater than
Column B at
this point, but keep in mind that there were no stipulations on what x
or y could be. This means they can
be ANY real number. So if there product is positive, then Column A
would be greater, but if there product is negative, then Column B would be
greater.
The relationship cannot be determined from the information
given.
Need more help on these topics? Multiplying
Polynomials
|
Column A
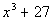 |
Column B
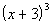 |
 Answer:
D Answer:
D
Cubing Column B we get:
|
It is real tempting to say that Column B is greater than
Column A at this point, but keep in mind that there were no stipulations on what x could be. This means it can be ANY real number. So if 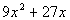 is positive, then Column B would be greater, but if it is negative,
then Column A would be greater. Both are possible.
The relationship cannot be determined from the information
given.
Need more help on these topics? Multiplying
Polynomials
|
Column A
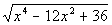 |
Column B
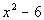 |
 Answer:
D Answer:
D |
|
*Factor the Perfect Square Trinomial
*The sq. root of an expression
squared is the abs. value of that expression
|
If 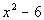 is positive,
then the two values are the same. However, if it is negative
then, Column A will be greater.
The relationship cannot be determined from the information
given.
Need more help on these topics? Factoring
and Square Root
|

WTAMU > Virtual Math Lab > GRE Math
Disclaimer:
Note that we can not
guarantee that you will pass your test after going through any of the tutorials
in this website. However, it will definitely help you to better
understand the topics covered. WTAMU and Kim Seward are not responsible
for how a student does on any test for any reason including not being able
to access the website due to any technology problems.
GRE and Graduate Record Examination are the
registered trademarks of Educational Testing Service (ETS). The material here has
neither been reviewed nor endorsed by ETS.
Throughout this website, we link to various
outside sources.
WTAMU and Kim Seward do not have any ownership to any of these outside
websites and cannot give you permission to make any kind of copies of
anything found at any of these websites that we link to. It is purely for
you to link to for information or fun as you go through the study
session. Each of these websites have a copy right clause that you need to read
carefully if you are wanting to do anything other than go to the website and read
it. We discourage any illegal use of the webpages found at these
sites.
|
All contents copyright (C) 2003 - 2008, WTAMU and Kim Seward. All rights reserved.
Last revised on November 24, 2008 by Kim Seward.
|
|
|


