College Algebra
Answer/Discussion to Practice Problems
Tutorial 52: Solving Systems of
Nonlinear Equations
in Two Variables
 Answer/Discussion
to 1a Answer/Discussion
to 1a
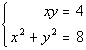
|
I'm going to chose to use the substitution method.
Not that because of the terms involved, it would not be possible to
work this problem using the process of elimination. |
Both of these equations are already simplified. No work needs
to be done here. |
It does not matter which equation or which variable you choose to solve
for. Just keep it simple.
I'm going to chose to use the first equation to solve for y.
Solving the first equation for y we get: |
|
*1st equation solved for y |
Substitute the expression 4/x for y into the second equation and solve for x:
(when you plug in an expression like this, it is just like you plug
in a number for your variable) |
Plug in both values found for x in step
4. |
Plug in -2 for x into the equation in
step 2 to find y's value. |
(-2, -2) is one solution to this system.
Plug in 2 for x into the equation in
step 2 to find y's value. |
(2, 2) is another solution to this system. |
You will find that if you plug either the ordered pair (-2, -2) OR
(2, 2) into BOTH equations of the original system, that they are both a
solution to BOTH of them.
(-2, -2) and (2, 2) are both a solution to our system. |
 Answer/Discussion
to 1b Answer/Discussion
to 1b
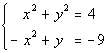
|
I'm going to chose to use the elimination by addition method, however
it would be perfectly find for you to use the substitution method.
Either way the answer will be the same. |
Both of these equations are already simplified. No work needs
to be done here. |
Again, you want to make this as simple as possible.
The variable that you want to eliminate must be a like variable. Note that x squareds' coefficients are
already opposites. So we do not have to multiply either equation
by a number.
Also note that the y terms are not like
terms so we would not be able to eliminate y in this problem.
Here is the original problem complete with opposite coefficients
for the x squared terms: |
|
*Note that x squareds
dropped out
|
|
*Setting the quadratic = 0
|
Note that this does not factor, so I'm going to have to use drastic
majors - yes the Quadratic Formula.
If you need a review on the quadratic formula feel free to go to Tutorial
17: Quadratic Equations. |
|
*Identifying a, b, and c for the quad. form.
*Plugging a, b,
and c into the quad form.
*Simplifying radicand, which is a negative
number
|
Note how we came up with a negative underneath the square root.
That means there is NOT a real number solution for this. |
There is no value to plug in here. |
There are no ordered pairs to check.
The answer is no solution. |
 Answer/Discussion
to 1c Answer/Discussion
to 1c
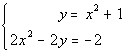
|
I'm going to chose to use the substitution method, however it would
be perfectly find for you to use the elimination by addition method.
Either way the answer will be the same. |
Both of these equations are already simplified. No work needs
to be done here. |
Note how the first equation is already solved for y.
We can use that one for this step.
It does not matter which equation or which variable you choose to solve
for. But it is to your advantage to keep it as simple as possible.
First equation solved for y: |
Substitute the expression 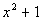 for y into the second equation and solve for x: for y into the second equation and solve for x:
(when you plug in an expression like this, it is just like you plug
in a number for your variable) |
|
*Sub. x^2 + 1
for y
*Distribute -2 through ( )
*Variable dropped out AND true |
Wait a minute, where did our variable go????
As mentioned before, if the variable drops out AND we have a TRUE statement,
then when have an infinite number of solutions. They end up being
the same line. |
Since we did not get a value for x, there
is nothing to plug in here. |
There is no value to plug in here.
When they end up being the same equation, you have an infinite number
of solutions. You can write up your answer by writing out either
equation to indicate that they are the same equation.
Two ways to write the answer are 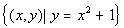 OR OR 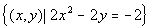 . . |

Last revised on April 25, 2011 by Kim Seward.
All contents copyright (C) 2002 - 2011, WTAMU and Kim Seward. All rights reserved.
|
|


