College Algebra
Answer/Discussion to Practice Problems
Tutorial 38: Zeros of Polynomial Functions, Part I:
Rational Zero Theorem and Descartes' Rule of Signs
 Answer/Discussion
to 1a Answer/Discussion
to 1a
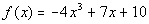
|
The factors of the constant term 10 are 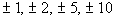 . |
The factors of the leading coefficient - 4 are 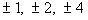 . |
Writing the possible factors as 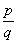 we get:
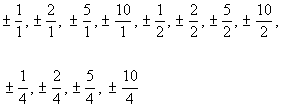
Note, how when you reduce down the fractions, some of them are repeated.
Here is a final list of all the POSSIBLE rational zeros, each one
written once and reduced:
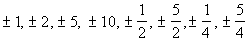
|
 Answer/Discussion
to 2a Answer/Discussion
to 2a
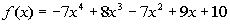
|
In this problem it isn't asking for the zeros themselves, but what
are the possible number of them. This can help narrow down your possibilities
when you do go on to find the zeros.
Possible number of positive real
zeros:
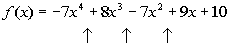
The up arrows are showing where there are sign changes between successive
terms, going left to right. The first arrow on the left shows a sign
change from negative 7 to positive 8. The 2nd arrow shows a sign
change from positive 8 to negative 7. The third arrow shows a sign
change from negative 7 to positive 9.
There are 3 sign changes between successive terms, which means that
is the highest possible number of positive real zeros. To find the
other possible number of positive real zeros from these sign changes, you
start with the number of changes, which in this case is 3, and then go
down by even integers from that number until you get to 1 or 0.
Since we have 3 sign changes with f(x),
then there are possibility of 3 or 3 - 2 = 1 positive real zeros. |
Possible number of negative
real zeros:
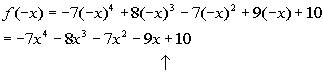
The up arrow is showing where there is a sign change between successive
terms, going left to right. This arrow shows a sign change from negative
9 to positive 10.
There is only 1 sign change between successive terms, which means that
is the highest possible number of negative real zeros. To find the
other possible number of negative real zeros from these sign changes, you
start with the number of changes, which in this case is 1, and then go
down by even integers from that number until you get to 1 or 0.
If we went down by even integers form 1, we would be in the negative
numbers, which is not a feasible answer, since we are looking for the possible
number of negative real zeros. In other words, we can't have a -1
of them.
Therefore, there is exactly 1 negative real zero. |
 Answer/Discussion
to 3a Answer/Discussion
to 3a
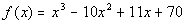
|
List all of the possible zeros:
The factors of the constant term 70 are 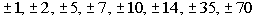 . .
The factors of the leading coefficient 1 are 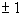 . .
Writing the possible factors as 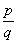 we get: we get:
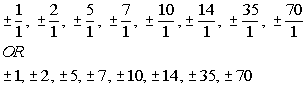
|
Before we try any of these, let's apply Descartes' Rule of Signs to
see if it can help narrow down our search for a rational zero.
Possible number of positive real
zeros:
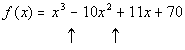
The up arrows are showing where there are sign changes between successive
terms, going left to right.
There are 2 sign changes between successive terms, which means that
is the highest possible number of positive real zeros. To find the
other possible number of positive real zeros from these sign changes, you
start with the number of changes, which in this case is 2, and then go
down by even integers from that number until you get to 1 or 0.
Since we have 2 sign changes with f(x),
then there are possibility of 2 or 2 - 2 = 0 positive real zeros. |
Possible number of negative
real zeros:
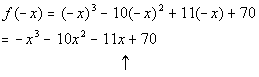
There is only 1 sign change between successive terms, which means that
is the highest possible number of negative real zeros. To find the
other possible number of negative real zeros from these sign changes, you
start with the number of changes, which in this case is 1, and then go
down by even integers from that number until you get to 1 or 0.
If we went down by even integers form 1, we would be in the negative
numbers, which is not a feasible answer, since we are looking for the possible
number of negative real zeros. In other words, we can't have a -1
of them.
Therefore, there is exactly 1 negative real zero. |
Use synthetic division to test
the possible zeros and find an actual zero:
Recall that if you apply synthetic division and the remainder is 0,
then c is a zero or root of the polynomial
function.
If you need a review on synthetic division, feel free to go to Tutorial
37: Synthetic Division and the Remainder and Factor Theorems.
At this point you are wanting to pick any POSSIBLE rational root form
the list of 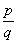 .
Above, we found that there is exactly 1 negative rational zero. Since
we know that there is one for sure, then we may want to go ahead and start
with trying positive rational roots. I would suggest to start
with smaller easier numbers and then go from there. .
Above, we found that there is exactly 1 negative rational zero. Since
we know that there is one for sure, then we may want to go ahead and start
with trying positive rational roots. I would suggest to start
with smaller easier numbers and then go from there.
I'm going to choose -1 to try:
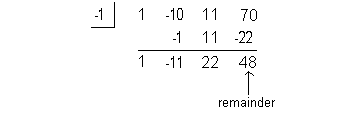
Since the reminder came out 48, this means f(-1)
= 48, which means x = -1 is NOT a zero for
this polynomial function.
That doesn't mean that we pack up our bags and quit. It's back
to the drawing board.
We need to choose another number that comes from that same list of POSSIBLE
rational roots.
This time I'm going to choose -2:
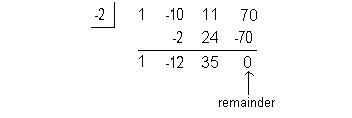
At last, we found a number that has a remainder of 0. This means that x = -2 is a zero or root of our polynomial function. |
Use the actual zero to find
all the zeros:
Since, x = -2 is a zero, that means x + 2 is a factor of our polynomial function.
Rewriting f(x)
as (x + 2)(quotient) we get:
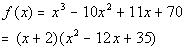
We need to finish this problem by setting this equal to zero and
solving it: |
|
*Set 1st factor = 0
*Set 2nd factor = 0
*Set 3rd factor = 0
|
The zeros of this function are x = -2,
5, and 7. |
 Answer/Discussion
to 3b Answer/Discussion
to 3b
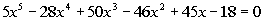
|
List all of the possible zeros:
The factors of the constant term -18 are 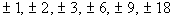 . .
The factors of the leading coefficient 5 are 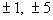 . .
Writing the possible factors as 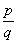 we get: we get:
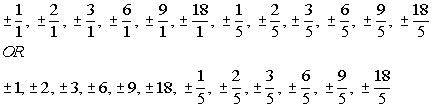
|
Before we try any of these, let's apply Descartes' Rule of Signs to
see if it can help narrow down our search for a rational zero.
Possible number of positive real
zeros:
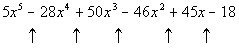
The up arrows are showing where there are sign changes between successive
terms, going left to right.
There are 5 sign changes between successive terms, which means that
is the highest possible number of positive real zeros. To find the
other possible number of positive real zeros from these sign changes, you
start with the number of changes, which in this case is 5, and then go
down by even integers from that number until you get to 1 or 0.
Since we have 5 sign changes with f(x),
then there are possibility of 5, 5 - 2 = 3, or 5 - 4 = 1 positive real
zeros. |
Possible number of negative
real zeros:
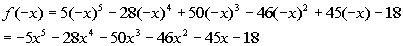
There are no sign changes.
This means there are no negative real zeros. |
Use synthetic division to test
the possible zeros and find an actual zero:
Recall that if you apply synthetic division and the remainder is 0,
then c is a zero or root of the polynomial
function.
If you need a review on synthetic division, feel free to go to Tutorial
37: Synthetic Division and the Remainder and Factor Theorems.
At this point you are wanting to pick any POSSIBLE rational root from
the list of 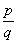 .
Above, we found that there are no negative rational zero. So we do
not need to try any negative numbers. I would suggest to start with
smaller easier numbers and then go from there. .
Above, we found that there are no negative rational zero. So we do
not need to try any negative numbers. I would suggest to start with
smaller easier numbers and then go from there.
I'm going to choose 2 to try:
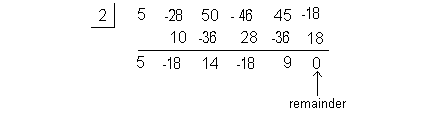
Bingo!!!! We found a number that has a remainder of 0. This means
that x = 2 is a zero or root of our polynomial
function. |
Use the actual zero to find
all the zeros:
Since, x = 2 is a zero, that means x - 2 is a factor of our polynomial function.
Rewriting f(x)
as (x - 2)(quotient) we get:
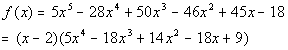
We need to finish this problem by setting this equal to zero and
solving it: |
Looks like we can't factor this one. We are going to have to
repeat this process again, but this time we will use this factor that we
found.
Recall, that in Descartes's Rule of Signs we already found that there
is no negative real zeros. So when we go trying again we can focus
on finding another positive real zero.
Note that we can still pick from the same list of 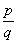 numbers as we did above or narrow the list down with the new constant.
When we set up the synthetic division, we will just look at the remaining
factor, to help us factor that down farther. numbers as we did above or narrow the list down with the new constant.
When we set up the synthetic division, we will just look at the remaining
factor, to help us factor that down farther.
Note that the new constant term is 9. That means we can narrow
down our list of 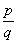 . .
The factors of the constant term 9 are 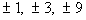 . .
The factors of the leading coefficient 5 are 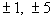 . .
Writing the possible factors as 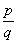 we get: we get:
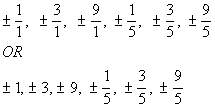
Note that we can still pick from the same list of 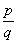 numbers as we did above, since we are still looking at solving the same
overall problem, but this list is a shorter one to pick from. Note how
all of the numbers in this list also belong to the list above. numbers as we did above, since we are still looking at solving the same
overall problem, but this list is a shorter one to pick from. Note how
all of the numbers in this list also belong to the list above.
I'm going to choose 3 to try:
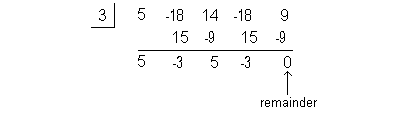
Bingo!!!! We found a number that has a remainder of 0. This means that x = 3 is a zero or root of our polynomial function. |
Use the actual zero to find
all the zeros:
Since, x = 3 is a zero, that means x - 3 is a factor of our polynomial function.
Rewriting f(x)
as (x - 2)(x -
3)(quotient) we get:
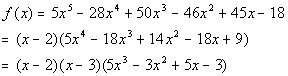
We need to finish this problem by setting this equal to zero and
solving it: |
|
*Set 1st factor = 0
*Set 2nd factor = 0
*Set 3rd factor = 0
*Set 4th factor = 0
|
The zeros of this function are x = 2,
3, i, -i, and 3/5. |

Last revised on March 15, 2010 by Kim Seward.
All contents copyright (C) 2002 - 2012, WTAMU and Kim Seward. All rights reserved.
|
|


