College Algebra
Answer/Discussion to Practice Problems
Tutorial 34:Graphs of Quadratic Functions
 Answer/Discussion
to 1a Answer/Discussion
to 1a
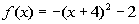
|
|
*Standard form of quad. function |
Since (h, k)
is the vertex in standard form, what do you think our vertex is for this
problem?
If you said (- 4, -2) you are correct.
Be careful about your signs on this problem. Notice how the sign
in front of h is a minus, but the one in front
of k is positive. So h is the number we are subtracting from x, which
in our case is negative 4. k is the number
we are adding at the end, which our case we are adding a negative 2. |
Maximum or Minimum?
Next we want to determine if the vertex that
we found, (- 4, -2), is a maximum or minimum point, without graphing.
If we know which direction the curve opens, that
can help us answer this question.
Since a = -1, and
-1 is less than 0, this parabola would open down  . .
So does that mean the vertex is a maximum or minimum
point?
If you said a maximum point, you are right on.
So our vertex (- 4, -2) is the maximum point. |
 Answer/Discussion
to 1b Answer/Discussion
to 1b
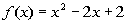
|
|
*Identify a, b,
and c
*Plug values into vertex form. for a, b,
and c
*Plug 1 in for x to find the y value of the vertex |
The vertex would be (1, 1). |
Maximum or Minimum?
Next we want to determine if the vertex that
we found, (1, 1) , is a maximum or minimum point, without graphing.
If we know which direction the curve opens, that
can help us answer this question.
Since a = 1, and 1
is greater than 0, this parabola would open up  . .
So does that mean the vertex is a maximum or minimum
point?
If you said a minimum point, you are right on.
So our vertex (1, 1) is the minimum point. |
 Answer/Discussion
to 2a Answer/Discussion
to 2a
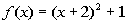
|
Since a = 1 and 1 > 0, then it looks like it
is going to curve up.
This gives us a good reference to know we are going in the right direction. |
|
*Standard form of quad. function
|
Since (h, k)
is the vertex in standard form, what do you think our vertex is?
If you said (-2, 1) you are correct.
Be careful about your signs on this problem. Notice how
the sign in front of h is a minus, but the
one in front of k is positive. So h is
the number we are subtracting from x, which
in our case is -2. k is the number we
are adding at the end, which our case we are adding a 1. |
y-intercept
Reminder that the y-intercept is always
where the graph crosses the y-axis which means x = 0: |
The y-intercept is (0, 5).
x-intercept
Reminder that the x-intercept is always
where the graph crosses the x-axis which means y = 0: |
|
*Replace y (or
f(x)) with 0
|
Note that this does not factor. Let's try solving by using
the quadratic formula: |
|
*Plug in values for a, b,
and c
|
Note how we got a negative number underneath the square root.
That means there is no real number solution. That also means that
there are NO x-intercepts. |
Axis of symmetry
As shown on the graph, the axis of symmetry is x = -2. |
 Answer/Discussion
to 2b Answer/Discussion
to 2b
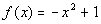
|
Since a = -1 and -1 < 0, then it looks
like it is going to curve down.
This gives us a good reference to know we are going in the right direction. |
|
*Identify a, b,
and c
*Plug values into vertex form. for a, b,
and c
*Plug 0 in for x to find the y value of the vertex |
y-intercept
Reminder that the y-intercept is always
where the graph crosses the y-axis which means x = 0: |
The y-intercept is (0, 1).
x-intercept
Reminder that the x-intercept is always
where the graph crosses the x-axis which means y = 0: |
The x-intercepts are (-1, 0) and (1,
0). |
Axis of symmetry
As shown on the graph, the axis of symmetry is x = 0. |

Last revised on July 10, 2010 by Kim Seward.
All contents copyright (C) 2002 - 2010, WTAMU and Kim Seward. All rights reserved.
|
|


