Answer/Discussion to 1a

The larger of two numbers is 5 more than twice the smaller.  If the smaller is subtracted from the larger, the result is 12.  Find the numbers.

Since we are looking for two numbers, we will let 

x = the smaller number 

y = the larger number

Equation (1):

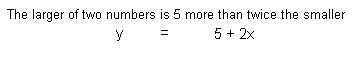
Equation (2):

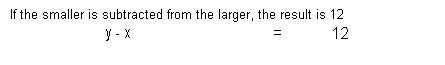
No simplification is needed for this problem. 
 

I'm going to go ahead and have us use the substitution method as shown in Tutorial 19: Solving Systems of Linear Equations in Two Variables to solve this.

Solve one equation for either variable
Since equation (1) is nicely solved for y, we will use that to substitute into the other equation.

y = 5 + 2x  (1)
 

Substitute what you get above into the other equation AND solve for the remaining variable.

Substituting in 5 + 2x for y into equation (2) and solving for x we get:

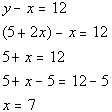
*Inverse of add 5 is sub. 5
 

Using equation (1) to plug in 7 for x and solving for y we get:

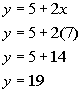
Final Answer:
The numbers are 7 and 19.

(return to problem 1a)

Answer/Discussion to 1b

It takes a boat 2 hours to travel 24 miles downstream and 3 hours to travel 18 miles upstream.  What is the speed of the boat in still water and of the current of the river?

Since we are looking for two different rates, we will let 

x = rate of the boat

y = the rate of the current

Since this is a rate/distance problem, it might be good to organize our information using the distance formula.

Keep in mind that the rate of the current is affecting the overall speed. 

When the boat is going upstream, it will be going slower.  That rate will be x - y. 

When the boat is going downstream, it will be going faster.  That rate will be x + y.
 
 

Equation (1):

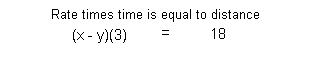
Equation (2):

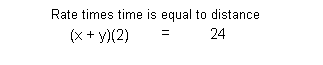
Simplify if needed. 

We can simplify this by dividing both sides of equation (1) by 3 and equation (2) by 2:

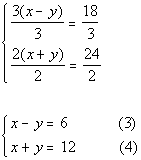
*Div. both sides of eq. (2) by 2
 
 
 

Multiply one or both equations by a number that will create opposite coefficients for either x or y if needed AND add the equations.

Since we already have opposite coefficients on y, we can go right into adding equations (3) and (4) together:

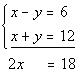
*y's dropped out

Solving for x we get:

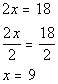
Using equation (4) to plug in 9 for x and solving for y we get:

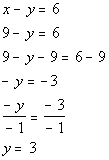
*Inverse of mult. by -1 is div. by -1

Final Answer:
The boat speed is 9 mph and the rate of the current is 3 mph.

(return to problem 1b)

Answer/Discussion to 1c

A student has money in three accounts that pay 5%, 7%, and 8%, in annual interest.  She has three times as much invested at 8% as she does at 5%.  If the total amount she has invested is $1600 and her interest for the year comes to $115, how much money does she have in each account?

Since we are looking for three different amounts, we will let 

x = the amount invested at 5%

y = the amount invested at 7%

z = the amount invested at 8%

Equation (1):

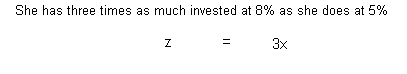
Equation (2):

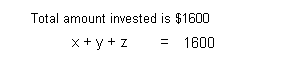
Equation (3):

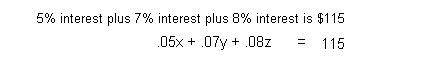
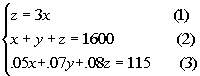
Simplify and put all three equations in the form Ax + By  + Cz = D if needed.

Equation (1) needs to be put in the correct form and equation (3) needs to be multiplied by 100 to get rid of the decimals:

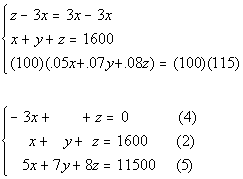
*Mult. both sides of eq. (3)by 100
 
 
 

Since y is already eliminated in equation (4), it would be quickest and easiest to eliminate y.

We can use equation (4) as one equation with y eliminated

Multiplying equation (2) by -7 and adding it to equation (5) we get:

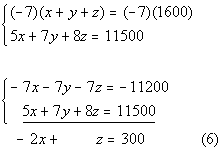
*y's have opposite coefficients

*y's dropped out

Putting those two equations together we get:

Multiplying equation (6) by -1 and then adding that to equation (4) we get:

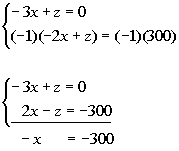
*z's have opposite coefficients

*z's dropped out

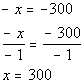
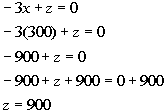
*Inverse of sub. 900 is add 900
 

Using equation (2) to plug in 300 for x and 900 for z we get:

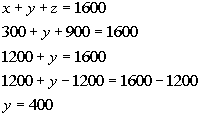
*Inverse of add 1200 is sub. 1200
 

Final Answer:
$300 is invested at 5%, $400 is invested at 7% and $900 is invested at 8%.

(return to problem 1c)