Intermediate Algebra
Answer/Discussion to Practice Problems
Tutorial 10: Linear Inequalities
 Answer/Discussion
to 1a |
|
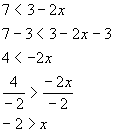
Interval notation: (- ,
-2)
Graph:
 |
*Inv. of add 3 is sub. 3
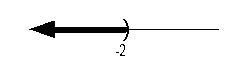
*Inv. of mult. by -2 is div. both sides by
-2, so reverse inequality sign
*Open interval indicating all values less than
-3
*Visual showing all numbers less than -2 on
the number line
|
Notice how our variable was on the right side of the inequality.
It doesn't matter what side you have the variable on, as long as it by
itself on one side and everything else is on the other side. What
you do have to be careful about is putting it in interval notation and
graphing it properly. It is almost like reading it backwards this
way. So, if you feel more comfortable writing it with your variable
on the left side, by all means, go ahead and do that.
Interval notation:
We have an open interval since there we are not including where it
is equal to -2. x is less than
-2, so -2 is our largest value of the interval so it goes on the right.
Since there is no lower endpoint (it is ALL values less than -2), we put
the negative infinity symbol on the left side. The curved end on
-2 indicates an open interval. Negative infinity always has a curved
end because there is not an endpoint on that side.
Graph:
We use the same type of notation on the endpoint as we did in the interval
notation, a curved end. Since we needed to indicate all values
less than -2, the part of the number line that was to the left of -2 was
darkened.
(return to
problem 1a) |
Answer/Discussion
to 1b |
|
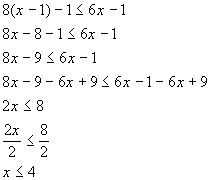
Interval notation: (-,
4]
Graph:
 |
*Distributive property
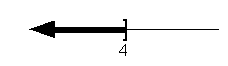
*Get x terms on one side, constants
on the other side
*Inv. of mult. by 2 is div. both sides by 2
*Closed interval indicating all values less
than or equal to 4
*Visual showing all numbers less than or equal
to 4 on the number line
|
Interval notation:
This time we have a closed interval since we are including where it
is equal to 4. x is less than or
equal to 4, so 4 is our largest value of the interval so it goes
on the right. Since there is no lower endpoint (it is ALL values
less than or equal to 4), we put the negative infinity symbol on the left
side. The boxed end on 4 indicates a closed interval. Negative
infinity always has a curved end because there is not an endpoint on that
side.
Graph:
Again, we use the same type of notation on the endpoint as we did in
the interval notation - a boxed end. Since we needed to indicate
all values less than or equal to 4, the part of the number line that was
to the left of 4 was darkened.
(return to
problem 1b) |
Answer/Discussion
to 1c |
|
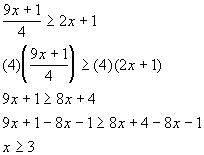
Interval notation: [3, )
Graph:
 |
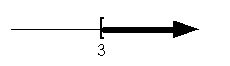
*Mult. both sides by the LCD
*Get x terms on
one side, constants on the other
*Closed interval indicating all values greater
than or equal to 3
*Visual showing all numbers greater than or
equal to 3 on the number line
|
Interval notation:
Since we are including where it is equal to 3, we have a closed
interval . x is greater than or
equal to 3, so 3 is our smallest value of the interval so it goes on the
left. Since there is no upper endpoint (it is ALL values greater
than or equal to 3), we put the infinity symbol on the right side.
The boxed end on 3 indicates a closed interval. Infinity always has
a curved end because there is not an endpoint on that side.
Graph:
Again, we use the same type of notation on the endpoint as we did in
the interval notation - a boxed end. Since we needed to indicate
all values greater than or equal to 3, the part of the number line that
was to the right of 3 was darkened.
(return to
problem 1c) |
Last revised on July 3, 2011 by Kim Seward.
All contents copyright (C) 2001 - 2011, WTAMU and Kim Seward.
All rights reserved.
|
|
