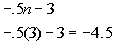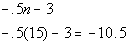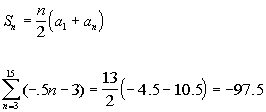College Algebra Tutorial 54
College Algebra
Answer/Discussion to Practice Problems
Tutorial 54C: Arithmetic Sequences and Series
 Answer/Discussion
to 1a
Answer/Discussion
to 1a
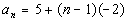
Since an arithmetic sequence is a sequence, you find
the terms exactly the same way that you do a sequence.
n is our term number and we
plug the term number into the function to find the value of the term.
If you need a review on sequences, feel free to go to
Tutorial 54A: Sequences.
Lets see what we get for
our first five terms:
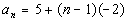
*n = 1
*n = 2
*n = 3
*n = 4
*n = 5
Note how the first term is 5.
What
was the common difference for this arithmetic sequence?
If you said -2 you are correct! Note how each term went DOWN
by 2 from the previous term.
Now lets check out the
15th term:
*n = 15
 Answer/Discussion
to 1b
Answer/Discussion
to 1b
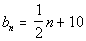
Since an arithmetic sequence is a sequence, you find
the terms exactly the same way that you do a sequence.
n is our term number and we
plug the term number into the function to find the value of the term.
If you need a review on sequences, feel free to go to
Tutorial 54A: Sequences.
Lets see what we get for
our first five terms:
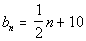
*n = 1
*n = 2
*n = 3
*n = 4
*n = 5
Note how the first term is 21/2.
What
was the common difference for this arithmetic sequence?
If you said 1/2 you are correct! Note how each term went up by
1/2 from the previous term.
Now lets check out the
15th term:
*n = 15
 Answer/Discussion
to 2a
Answer/Discussion
to 2a
0, .25, .5, .75, ...
We will use the
nth
term formula for an arithmetic sequence,
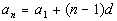 ,
, to
help us with this problem.
Basically we need to find two things, the first term of the sequence
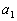
and the common
difference,
d.
What
is 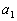
,
the
first term of the sequence?
If you said 0, give yourself a high five. The first term of
this sequence is 0.
What is d, the common
difference?
If you said .25, you are right!! Note that you would have to add
.25
to each previous term to get to the next term: 0 + .25 = .25, .25 + .25
= .5, and .5 + .25 = .75. It has to be consistent
throughout the
sequence.
Putting in 0 for 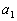 and .25 for d we get:
and .25 for d we get:
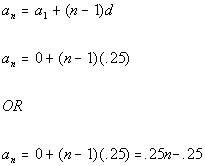
Either of these answers would give you the same arithmetic sequence.
 Answer/Discussion
to 2b
Answer/Discussion
to 2b
-5, -15, -25, -35, ...
We will use the
nth
term formula for an arithmetic sequence,
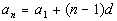 ,
, to
help us with this problem.
Basically we need to find two things, the first term of the sequence
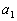
and the common
difference,
d.
What
is 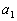
,
the
first term of the sequence?
If you said -5, give yourself a high five. The first term of
this sequence is -5.
What is d, the common
difference?
If you said -10, you are right!! Note that you would have to add
-10
to each previous term to get to the next term: -5 + (-10) = -15, -15 +
(-10)
= -25, and -25 + (-10) = -35. It has to be consistent
throughout the
sequence.
Putting in -5 for 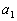 and -10 for d we get:
and -10 for d we get:
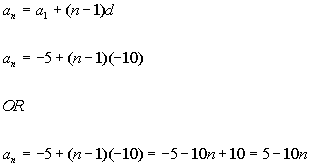
Either of these answers would give you the same arithmetic sequence.
 Answer/Discussion
to 3a
Answer/Discussion
to 3a
5 + 10 + 15 +.... + 500
We will use the formula for the sum of the first
n terms of an arithmetic
sequence,
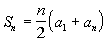 ,
, to
help us with this problem.
Basically we need to find three things: the first term of the sequence,
the last term of the sequence, and how many terms of the sequence we
are adding in the series.
What
is the first term?
If you said 5 you are right!
What is the last term?
If you said 500 give yourself a pat on the back.
How
many terms are we summing up?
If you said 100, you are correct. Because of the way it is written with
the 3 dots, this one is a little bit trickier. You have to do a
little figuring. We can use the
nth term of an arithmetic
sequence and solve for
n,
the number of terms in the sequence:
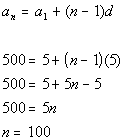 Putting in 5 for the first
term, 500 for the last term, and 100 for n, we get:
Putting in 5 for the first
term, 500 for the last term, and 100 for n, we get:
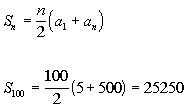
 Answer/Discussion
to 3b
Answer/Discussion
to 3b
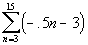
Note how
n starts at 3 and ends at 15. So we are looking for the sum of
terms 3 - 15.
We will use the formula for the sum of the first
n terms of an arithmetic
sequence,
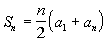 ,
, to
help us with this problem.
Basically we need to find three things: the first term of the sequence,
the last term of the sequence, and how many terms of the sequence we
are adding in the series.
What
is the first term?
If you said -4.5 you are right!
Since this summation starts at 3, you need to plug in 3 into the given
formula:
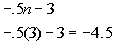 What
is the last term?
What
is the last term?
If you said -10.5 give yourself a pat on the back.
You get that by plugging 15 into the given formula:
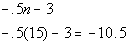 How
many terms are we summing up?
How
many terms are we summing up?
If you said 13, you are correct. If you start at 3 and go all the
way to 15, there will be 13 terms.
Putting in -4.5 for the
first term, -10.5 for the last term, and 13 for n, we get:
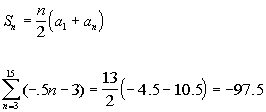

Last revised on May 16, 2011 by Kim Seward.
All contents copyright (C) 2002 - 2011, WTAMU and Kim Seward. All rights reserved.


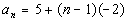
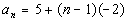
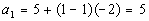
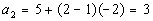
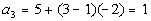
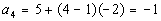
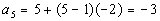
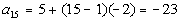
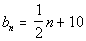
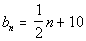
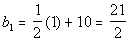
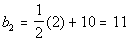
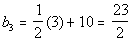
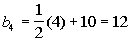
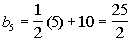
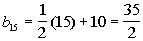
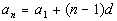 , to
help us with this problem.
, to
help us with this problem. 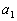 and the common
difference, d.
and the common
difference, d.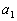 , the
first term of the sequence?
, the
first term of the sequence?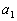 and .25 for d we get:
and .25 for d we get: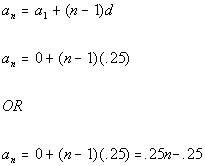
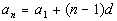 , to
help us with this problem.
, to
help us with this problem. 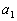 and the common
difference, d.
and the common
difference, d.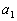 , the
first term of the sequence?
, the
first term of the sequence?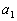 and -10 for d we get:
and -10 for d we get: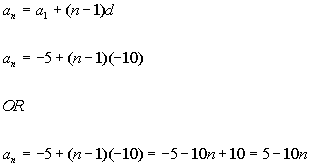
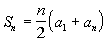 , to
help us with this problem.
, to
help us with this problem. 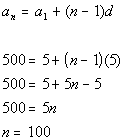
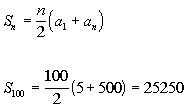
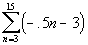
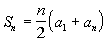 , to
help us with this problem.
, to
help us with this problem.