College Algebra
Tutorial 54C: Arithmetic Sequences and Series
 Learning Objectives Learning Objectives
After completing this tutorial, you should be able to:
- Know what an arithmetic sequence is.
- Find the nth
term of an arithmetic sequence.
- Write the formula for the nth term of an arithmetic
sequence.
- Calculate an arithmetic series.
|
 Introduction Introduction
In this tutorial we will mainly be going over
arithmetic sequences and series. We will be going forwards and
backwards with this. First we will be given the formula for the nth term and we will be
finding specified terms. Then we will turn it around and look at
the terms and find the formula for the nth term. We will finish up
by looking at arithmetic series. If you need a review on
sequences, feel free to go to Tutorial 54A: Sequences.
If you need a review on sequences, feel free to go to Tutorial 54B: Series. I
think that you are ready to move ahead. |
 Tutorial Tutorial
An arithmetic sequence is a sequence such that each
successive term is obtained from the previous term by addition or
subtraction of a fixed number called a common difference.
The sequence 4, 7, 10, 13, 16, ... is an example of an arithmetic
sequence. The pattern is that we are always adding a fixed number
of three to the previous term to get to the next term.
Be careful that you don't think that every sequence that has a pattern
in addition is arithmetic. It is arithmetic if you are always adding
the SAME number each time.
If you need a review on sequences, feel free to go to Tutorial
54A: Sequences.
|
nth or General Term
of an Arithmetic Sequence
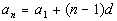
where 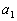 is the first term of the sequence
and d is the common
difference. is the first term of the sequence
and d is the common
difference.
|
 Example
1 Example
1: Find the first five terms and the15th term of
the arithmetic sequence 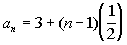 .
|
Since an arithmetic sequence is a sequence, you find
the terms exactly the same way that you do a sequence. n is our term number and we
plug the term number into the function to find the value of the term.
If you need a review on sequences, feel free to go to Tutorial 54A: Sequences.
Lets see what we get for
our first five terms:
|
Note how the first term is 3.
What
was the common difference for this arithmetic sequence?
If you said ½, you are correct! Note how each term went up
by 1/2 from the previous term.
Now lets check out the
15th term:
|
 Example 2 Example 2:
Find the first five terms and the15th term of the arithmetic sequence 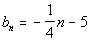 .
|
Since an arithmetic sequence is a sequence, you find
the terms exactly the same way that you do a sequence. n is our term number and we
plug the term number into the function to find the value of the term.
If you need a review on sequences, feel free to go to Tutorial 54A: Sequences.
Lets see what we get for
our first five terms:
|
Note how the first term is not -5, but -21/4. The
formula for the nth
term used n,
instead of n - 1 that is in the general
form 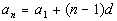 . So it was a simplified or adjusted form that was used.
What
was the common difference for this arithmetic sequence?
If you said -1/4 you are correct! Note how each term went DOWN by
1/4 from the previous term.
Now lets check out the
15th term:
|
 Example 3 Example 3:
Write a formula for the nth term of the arithmetic sequence -10, -5, 0,
5, ....
|
We will use the nth
term formula for an arithmetic sequence, 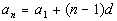 , , to
help us with this problem.
Basically we need to find two things, the first term of the sequence 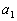 and the common difference, d.
What
is 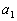 , the
first term of the sequence?
If you said -10, give yourself a high five. The first term of
this sequence is -10.
What is d, the common
difference?
If you said 5, you are right!! Note that you would have to add 5
to each previous term to get to the next term: -10 + 5 = -5, -5 + 5 =
0, and 0 + 5 = 5. It has to be consistent throughout the
sequence.
Putting in -10 for 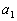 and 5 for d we get: and 5 for d we get:
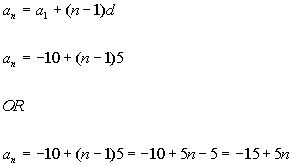
Either of these answers would give you the same arithmetic sequence.
|
 Example 4 Example 4:
Write a formula for the nth term of the arithmetic sequence 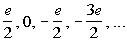
|
We will use the nth
term formula for an arithmetic sequence, 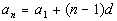 , , to
help us with this problem.
Basically we need to find two things, the first term of the sequence 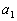 and the common
difference, d.
What
is 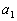 , the
first term of the sequence?
If you said 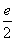 , give yourself a high five.
The first term of this sequence is 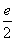 .
What is d, the common
difference?
If you said 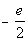 , you are
right!! Note that you would have to add 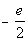 to
each previous term to get to the next term.
Putting in 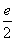 for for 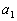 and and 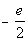 for d we get: for d we get:

Either of these answers would give you the same arithmetic sequence.
|
Arithmetic Series
The Sum of the First n Terms
of an Arithmetic Sequence
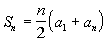
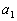 is the first term of the sequence and is the first term of the sequence and 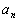 is the nth term of the sequence. is the nth term of the sequence.
|
 Example 5 Example 5:
Find the sum of the arithmetic series 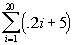 .
|
Note how i starts at 1 and ends at 20. So we are looking for the sum of
terms 1 - 20.
We will use the formula for the sum of the first n terms of an arithmetic
sequence, 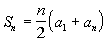 , , to
help us with this problem.
Basically we need to find three things: the first term of the sequence,
the last term of the sequence, and how many terms of the sequence we
are adding in the series.
What
is the first term?
If you said 5.2 you are right!
You get that by plugging 1 into the given formula:
.2 i + 5
.2(1) + 5 = 5.2
What
is the last term?
If you said 9, give yourself a pat on the back.
You get that by plugging 20 into the given formula:
.2 i + 5
.2(20) + 5 = 9
How
many terms are we summing up?
If you said 20, you are correct. If you start at 1 and go all the
way to 20, there will be 20 terms.
Putting in 5.2 for the
first term, 9 for the last term, and 20 for n, we get:
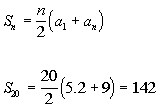
|
 Example 6 Example 6:
Find the sum of the arithmetic series 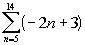 .
|
Note how n starts at 5 and ends at 14. So we are looking for the sum of
terms 5 - 14.
We will use the formula for the sum of the first n terms of an arithmetic
sequence, 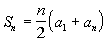 , , to
help us with this problem.
Basically we need to find three things: the first term of the sequence,
the last term of the sequence, and how many terms of the sequence we
are adding in the series.
What
is the first term?
If you said -7 you are right!
Since this summation starts at 5, you need to plug in 5 into the given
formula:
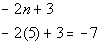 What
is the last term?
What
is the last term?
If you said -25 give yourself a pat on the back.
You get that by plugging 14 into the given formula:
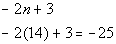 How
many terms are we summing up?
How
many terms are we summing up?
If you said 10, you are correct. If you start at 5 and go all the
way to 14, there will be 10 terms.
Putting in -7 for the
first term, -25 for the last term, and 10 for n, we get:
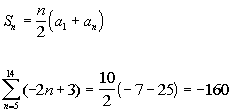
|
 Example 7 Example 7:
Find the sum of the arithmetic series 3 + 6 + 9 + .... + 99.
|
We will use the formula for the sum of the first n terms of an arithmetic
sequence, 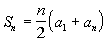 , , to
help us with this problem.
Basically we need to find three things: the first term of the sequence,
the last term of the sequence, and how many terms of the sequence we
are adding in the series.
What
is the first term?
If you said 3 you are right!
What is the last term?
If you said 99 give yourself a pat on the back.
How
many terms are we summing up?
If you said 33, you are correct. Because of the way it is written with
the 3 dots, this one is a little bit trickier. You have to do a
little figuring. We can use the nth term of an arithmetic
sequence and solve for n,
the number of terms in the sequence:
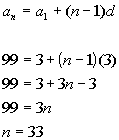 Putting in 3 for the first
term, 99 for the last term, and 33 for n, we get:
Putting in 3 for the first
term, 99 for the last term, and 33 for n, we get:
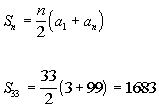
|
 Practice Problems Practice Problems
These are practice problems to help bring you to the next level.
It will allow you to check and see if you have an understanding of these
types of problems. Math works just like anything
else, if you want to get good at it, then you need to practice it.
Even the best athletes and musicians had help along the way and lots of
practice, practice, practice, to get good at their sport or instrument.
In fact there is no such thing as too much practice.
To get the most out of these, you should work the problem out on
your own and then check your answer by clicking on the link for the answer/discussion
for that problem. At the link you will find the answer
as well as any steps that went into finding that answer. |
 Practice Problems 1a - 1b: Find
the first five terms and the 15th term of the given arithmetic sequence. Practice Problems 1a - 1b: Find
the first five terms and the 15th term of the given arithmetic sequence.
 Practice Problems 2a - 2b:Write a
formula for the nth term of the given arithmetic sequence. Practice Problems 2a - 2b:Write a
formula for the nth term of the given arithmetic sequence.
 Practice Problems 3a - 3b: Find the
given term of the
expansion. Simplify the results. Practice Problems 3a - 3b: Find the
given term of the
expansion. Simplify the results.
 Need Extra Help on these Topics? Need Extra Help on these Topics?

Last revised on May 17, 2011 by Kim Seward.
All contents copyright (C) 2002 - 2011, WTAMU and Kim Seward. All rights reserved.
|
|


