College Algebra
Tutorial 46: Logarithmic Equations
 Learning Objectives
After completing this tutorial, you should be able to:
- Solve logarithmic equations.
|
Introduction
In this tutorial I will step you through how to solve equations that
have logarithmic expressions. In these equations, you will notice
that the variable that we are solving for is inside the log expressions.
We will rewrite the log equation exponentially using the definition of
logs to help us get the x outside of the log.
If you need a review on the definition of log functions, feel free to go
to Tutorial 43: Logarithmic Functions.
Ready, set, GO!!!!! |
Tutorial
|
Solving a Logarithmic Equation of the Form
|
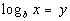
Step 1: Write as
one log isolated on one side. |
Get your log on one side everything outside of the log on the other
side of your equation using inverse operations.
Also use properties of logs to write it so that there is only one log.
If you need a review on properties of logs feel free to go to Tutorial
44: Logarithmic Properties. |
Step 2: Use
the definition of logarithms to write in exponential form. |
A reminder that the definition of logarithms is the logarithmic function
with base b, where b > 0 and b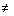 0,
and is defined as 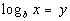if and only if  .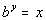
If you need a review on the definition of log functions, feel free to
go to Tutorial 43: Logarithmic
Functions. |
Now that the variable is out of the log, solve for the variable using
inverse operations to complete the problem. |
 Example
1: Solve the logarithmic equation  .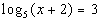
Round your answer to two decimal places. |
This is already done for us in this problem. |
 |
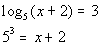*Rewrite in exponential form
*Base = 5 and exponent = 3 |
|
*5 cubed is 125
*Solve for x
|
Example
2: Solve the logarithmic equation  .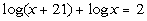
Round your answer to two decimal places. |
|
*Use the product
rule to write as one log
*one log is isolated |
|
*Rewrite in exponential form
*Base = 10 and exponent = 2 |
Remember that when there is no base written on a log, that means it
is the common log, or log base 10. If you need a review on common
logs feel free to go to Tutorial
43: Logarithmic Functions. |
Since -25 would create a negative number inside
both logs in this problem and we CANNOT take the log of a negative number,
we will have to throw out x = -25 as one of
our solutions.
Final answer: x = 4. |
Example
3: Solve the logarithmic equation  .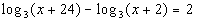
Round your answer to two decimal places. |
|
*Rewrite in exponential form
*Base = 3 and exponent = 2 |
|
*3 squared is 9
*Solve for x
*Multiply both sides by LCD of x + 2
|
Example
4: Solve the logarithmic equation  .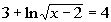
Round your answer to two decimal places. |
|
*Inverse of add 3 is sub. 3
*one log is isolated |
|
*Rewrite in exponential form
*Base = e and
exponent = 1 |
Remember that when you have ln, that means it is the natural log, or
log base e. If you need a review on natural
logs feel free to go to Tutorial
43: Logarithmic Functions. |
|
*Square both sides to get rid of the radical
*Solve for x
*Use the calculator to find e squared
|
Practice Problems
These are practice problems to help bring you to the next level.
It will allow you to check and see if you have an understanding of these
types of problems. Math works just like anything
else, if you want to get good at it, then you need to practice it.
Even the best athletes and musicians had help along the way and lots of
practice, practice, practice, to get good at their sport or instrument.
In fact there is no such thing as too much practice.
To get the most out of these, you should work the problem out on
your own and then check your answer by clicking on the link for the answer/discussion
for that problem. At the link you will find the answer
as well as any steps that went into finding that answer. |
 Practice Problems 1a - 1d: Solve the logarithmic equation. Round your
answer to two decimal places.
Need Extra Help on these Topics?
Last revised on March 24, 2011 by Kim Seward.
All contents copyright (C) 2002 - 2011, WTAMU and Kim Seward. All rights reserved.
|
|
