College Algebra
Answer/Discussion to Practice Problems
Tutorial 29: Circles
 Answer/Discussion
to 1a
Center (9, -10) and r = 5 |
What are the two things we need to write an equation of a circle????
If you said the center and the radius, you are correct.
Looks like we have all the information we need. We are ready to
put our equation together.
What value are we going to replace h with?
If you said 9, you are correct!!! h is the first number of the ordered pair of the center of the circle.
What value are we going to replace k with?
If you said -10, you are right on!!! k is the second number of the ordered pair of the center of the circle.
What value are we going to replace r with?
If you said 5, give yourself a pat on the back!!! r is the radius of the circle.
Putting it into standard form we get: |
|
*Plug in 9 for h,
-10 for k, and 5 for r
*5 squared is 25
*Standard form of circle with center (9, -10)
and
radius of 5
|
Make sure that you are careful when one of
your values is negative and you have to subtract it as we did in line 2. y - (-10) is not the same as y -
10. |
Answer/Discussion
to 1b
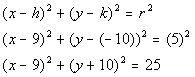
Center (2, 0) and |
What are the two things we need to write an equation of a circle????
If you said the center and the radius, you are correct.
Looks like we have all the information we need. We are ready to
put our equation together.
What value are we going to replace h with?
If you said 2, you are correct!!! h is the first number of the ordered pair of the center of the circle.
What value are we going to replace k with?
If you said 0, you are right on!!! k is the second number of the ordered pair of the center of the circle.
What value are we going to replace r with?
If you said ,
give yourself a pat on the back!!! r is the radius of the circle.
Putting it into standard form we get: |
|
*Plug in 2 for h,
0 for k, and sq. root of 2 for r
*sq. root of 2 squared is 2
*Standard form of circle with center (2, 0)
and radius sq. root of 2
|
Generally, when you have an expression where you are subtracting 0,
you can simplify it by not writing the - 0. Going from line 2 to
3 above, I simplified the expression y - 0
by writing it in the equivalent form,  . |
Answer/Discussion
to 2a
|
The equation is already in standard form. |
|
*Standard form of circle
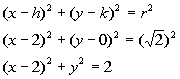
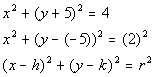
*4 is 2 squared
|
Make sure that you are careful. The
original standard form is  ,
where we have x MINUS h and y MINUS k.
So h is the number that we are subtracting
from x and k is
the number that we are subtracting from y.
Also, the right side of the equation is r SQUARED.
So in line 2 above, I rewrote the equation
to show what numbers we were actually subtracting on the left side of the
equation.
On the right side of the equation I showed
what number was being squared. This is to help you see how we get
the center (h, k)
and the radius (r).
Make sure that you are careful when one of
your values is negative and you have to subtract it as we did in line 2. y - (-5) is not the same as y -
5.
What value is h?
If you said 0, you are correct!!! Since
there is no value being subtracted from x in
the first ( ) that means it is understood that 0 is the number being
subtracted, that is the value of h.
What value is k?
If you said -5, you are right on!!! Since
-5 is the value being subtracted from y in
the second ( ), that is the value of k.
What value is r?
If you said 2, give yourself a pat on the back!!! Since 2 is
the number being squared on the right side of the standard form of our
equation, that is the value of r.
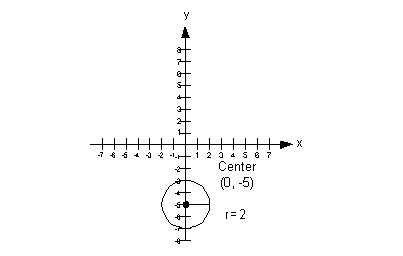
The center is (0, -5) and the radius is 2. |
Step 3: Graph,
if needed. |
Answer/Discussion
to 2b
|
The coefficients on the  and terms are both
already 1. |
|
*Inverse of add. 33 is sub. 33
|
|
*Complete the square for both x and y
*Make sure that you add 9 and 49 to BOTH sides |
Completing the square for x (as shown
above):
b is the coefficient of the -6x term, which in this case is -6. Complete the square by taking 1/2
of b and squaring it. Taking 1/2 of -6
we get -3, and then squaring -3 we get 9.
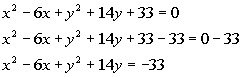
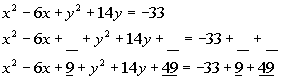
Completing the square for y (as shown
above):
b is the coefficient of the 14y term, which in this case is 14. Complete the square by taking 1/2
of b and squaring it. Taking 1/2 of 14
we get 7, and then squaring 7 we get 49. |
|
*Factor each PST
*Standard form of circle |
|
*Standard form of circle
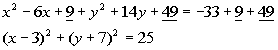
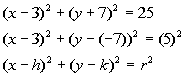
*25 is 5 squared
|
Make sure that you are careful. The
original standard form is ,
where we have x MINUS h and y MINUS k.
So h is the number that we are subtracting
from x and k is
the number that we are subtracting from y.
Also, the right side of the equation is r SQUARED.
So in line 2 above, I rewrote the equation
to show what numbers we were actually subtracting on the left side of the
equation.
On the right side of the equation I showed
what number was being squared. This is to help you see how we get
the center (h, k)
and the radius (r).
Make sure that you are careful when one of
your values is negative and you have to subtract it as we did in line 2. y - (-7) is not the same as y - 7.
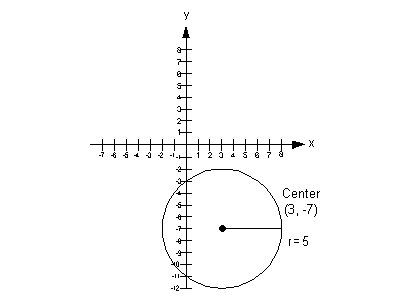
What value is h?
If you said 3, you are correct!!! Since
3 is the value being subtracted from x in the
first ( ), that is the value of h.
What value is k?
If you said -7, you are right on!!! Since
-7 is the value being subtracted from y in
the second ( ), that is the value of k.
What value is r?
If you said 5, give yourself a pat on the back!!! Since 5 is
the number being squared on the right side of the standard form of our
equation, that is the value of r.
The center is (3, -7) and the radius is 5. |
Step 3: Graph,
if needed. |
Last revised on Feb. 26, 2010 by Kim Seward.
All contents copyright (C) 2002 - 2010, WTAMU and Kim Seward. All rights reserved.
|
|
