

![]() Learning Objectives
Learning Objectives
![]() Introduction
Introduction
![]() Tutorial
Tutorial
![]()
(h, k)
is
the center
r is the radius
(x, y)
is
any point on the circle
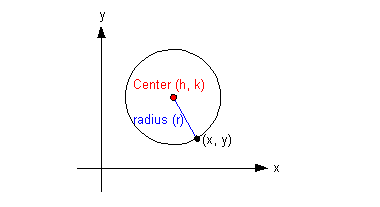
The h value of your center is the first value of your ordered pair and the k value of your center is the second value of your ordered pair.
When writing an equation of a circle, keep in mind that you ALWAYS need two pieces of information:
 Example
1: Write the standard form of the equation of the circle
with
center (5, 7) and r = 4.
Example
1: Write the standard form of the equation of the circle
with
center (5, 7) and r = 4.Looks like we have all the information we need. We are ready to put our equation together.
What value are we going to
replace h with?
If you said 5, you are correct!!! h is the first number of the ordered pair of the center of the circle.
What value are we going to
replace k with?
If you said 7, you are right on!!! k is the second number of the ordered pair of the center of the circle.
What value are we going to
replace r with?
If you said 4, give yourself a pat on the back!!! r is the radius of the circle.
Putting it into standard form we get:
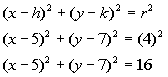
 Example
2: Write the standard form of the equation of the circle
with
center (-3, -1) and
Example
2: Write the standard form of the equation of the circle
with
center (-3, -1) and Looks like we have all the information we need. We are ready to put our equation together.
What value are we going to
replace h with?
If you said -3, you are correct!!! h is the first number of the ordered pair of the center of the circle.
What value are we going to
replace k with?
If you said -1, you are right on!!! k is the second number of the ordered pair of the center of the circle.
What value are we going to
replace r with?
If you said square root of 10, give yourself a pat on the back!!! r is the radius of the circle.
Putting it into standard form we get:

 Example
3: Write the standard form of the equation of the circle
with
center (0, 0) and r = 10.
Example
3: Write the standard form of the equation of the circle
with
center (0, 0) and r = 10.Looks like we have all the information we need. We are ready to put our equation together.
What value are we going to
replace h with?
If you said 0, you are correct!!! h is the first number of the ordered pair of the center of the circle.
What value are we going to
replace k with?
If you said 0, you are right on!!! k is the second number of the ordered pair of the center of the circle.
What value are we going to
replace r with?
If you said 10, give yourself a pat on the back!!! r is the radius of the circle.
Putting it into standard form we get:
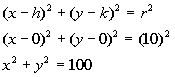
![]()
If your equation is in the general form you will need to complete the square to both the x terms and the y terms as if they were two separate problems.
Below is a review on completing the square. If you need more of a review on this topic, feel free to go to Tutorial 17: Quadratic Equations.
If the coefficient is not equal to 1, then divide both
sides by the
coefficients of the ![]() and
and![]() squared terms.
squared terms.
We need to find a number that we can add to the ![]() and x terms so that we have a PST.
We
also need to find a number that we can add to the
and x terms so that we have a PST.
We
also need to find a number that we can add to the ![]() and y terms so that we have a PST. We can get that magic number
by
doing the following:
and y terms so that we have a PST. We can get that magic number
by
doing the following:
If we have ![]() we
complete its square by adding
we
complete its square by adding ![]() to
both sides of the equation.
to
both sides of the equation.
In other words, we complete the square by taking
½ of b (the
coefficient of the x term) and then
squaring
it. Make sure you remember to add it to BOTH sides to keep the
equation
balanced. We do the same type of thing with the ![]() and y terms.
and y terms.
Since we will be completing the square for both the x’s and the y’s, we will have two numbers that we will be adding to both sides.
Keep in mind that when we use the letters h and k for our center, h is the first value of the ordered pair of the center. In other words, when you graph it, it corresponds to the x-axis. k is the second value of the ordered pair of the center. In other words, when you graph it, it corresponds to the y-axis.
 Example
4: Find the center and radius of the circle,
Example
4: Find the center and radius of the circle, 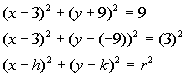
*9 is 3 squared
So, in line 2 above, I rewrote the equation to show what numbers we were actually subtracting on the left side of the equation.
On the right side of the equation I showed what number was being squared. This is to help you see how we get the center (h, k) and the radius (r).
Make sure that you are careful
when one of
your values is negative and you have to subtract it as we did in line
2. y - (-9) is not the same as y -
9.
What value is h?
If you said 3, you are correct!!! Since
3 is the value being subtracted from x in the
first ( ), that is the value of h.
What value is k?
If you said -9, you are right on!!! Since
-9 is the value being subtracted from y in
the second ( ), that is the value of k.
What value is r?
If you said 3, give yourself a pat on the back!!! Since 3 is
the number being squared on the right side of the standard form of our
equation, that is the value of r.
The center is (3, -9) and the radius is 3.

 Example
5: Find the center and radius of the circle,
Example
5: Find the center and radius of the circle, 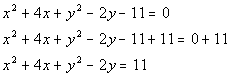
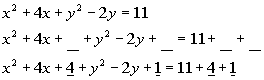
Completing the square for y (as
shown
above):
b is the coefficient of the -2y term, which in this case is -2. Complete the square by taking 1/2
of b and squaring it. Taking 1/2 of
-2
we get -1, and then squaring -1 we get 1.
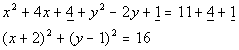
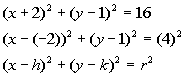
*16 is 4 squared
So in line 2 above, I rewrote the equation to show what numbers we were actually subtracting on the left side of the equation.
On the right side of the equation I showed what number was being squared. This is to help you see how we get the center (h, k) and the radius (r).
Make sure that you are careful
when one of
your values is negative and you have to subtract it as we did in line
2. x - (-2) is not the same as x - 2.
What value is h?
If you said -2, you are correct!!! Since
-2 is the value being subtracted from x in
the first ( ), that is the value of h.
What value is k?
If you said 1, you are right on!!! Since
1 is the value being subtracted from y in the
second ( ), that is the value of k.
What value is r?
If you said 4, give yourself a pat on the back!!! Since 4 is
the number being squared on the right side of the standard form of our
equation, that is the value of r.
The center is (-2, 1) and the radius is 4.
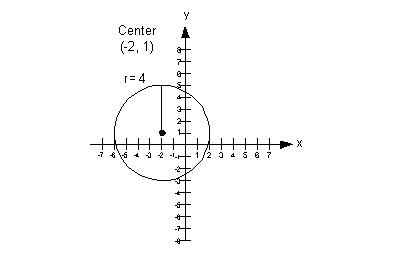
 Example
6: Find the center and radius of the circle,
Example
6: Find the center and radius of the circle, 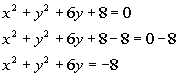
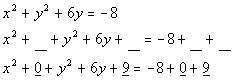
Completing the square for y (as
shown
above):
b is the coefficient of the 6y term, which in this case is 6. Complete the square by taking 1/2
of b and squaring it. Taking 1/2 of
6
we get 3, and then squaring 3 we get 9.
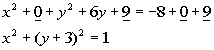
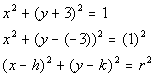
*16 is 4 squared
So in line 2 above, I rewrote the equation to show what numbers we were actually subtracting on the left side of the equation.
On the right side of the equation I showed what number was being squared. This is to help you see how we get the center (h, k) and the radius (r).
Make sure that you are careful
when one of
your values is negative and you have to subtract it as we did in line
2. y - (-3) is not the same as y - 3.
What value is h?
If you said 0, you are correct!!! Since
there is no value being subtracted from x in
the first ( ) that means it is understood that 0 is the number
being
subtracted, that is the value of h.
What value is k?
If you said -3, you are right on!!! Since
-3 is the value being subtracted from y in
the second ( ), that is the value of k.
What value is r?
If you said 1, give yourself a pat on the back!!! Since 1 is
the number being squared on the right side of the standard form of our
equation, that is the value of r.
The center is (0, -3) and the radius is 1.
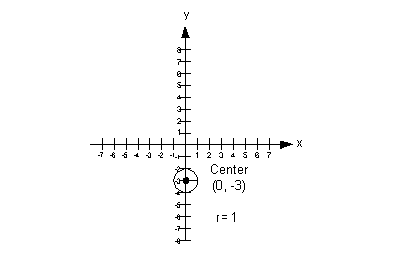
![]() Practice Problems
Practice Problems
To get the most out of these, you should work the problem out on your own and then check your answer by clicking on the link for the answer/discussion for that problem. At the link you will find the answer as well as any steps that went into finding that answer.
Practice Problems 1a - 1b: Write the standard form of the equation of the circle with the given conditions.
Practice Problems 2a - 2b: Find the center and radius of the given circle and graph it.
![]() Need Extra Help on these Topics?
Need Extra Help on these Topics?
Go to Get Help Outside the Classroom found in Tutorial 1: How to Succeed in a Math Class for some more suggestions.
Last revised on Feb. 26, 2010 by Kim Seward.
All contents copyright (C) 2002 - 2010, WTAMU and Kim Seward. All rights reserved.