College Algebra Tutorial 23


College Algebra
Answer/Discussion to Practice Problems  
Tutorial 23A: Quadratic Inequalities

WTAMU > Virtual Math Lab > College Algebra > Tutorial 23A: Quadratic Inequalities


 

 

checkAnswer/Discussion to 1a

problem 1a

I used the test-point method, but you could also use the sign graph of factors method.

 
Step 1: Write the quadratic inequality in standard form.

 
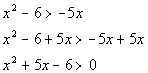
ad1a1

*Inv. of sub. 5x is add. 5x

 
 
Step 2: Solve the quadratic equation, quadratic equation, to get the boundary point(s).

 
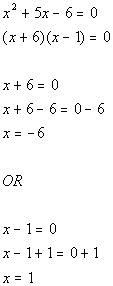
ad1a2

*Factor
 

*Set 1st factor = 0 and solve
 
 
 
 
 
 

*Set 2nd factor = 0 and solve
 

 


 
-6 and 1 are boundary points.

 
Step 3: Use the boundary point(s) found in step 2 to mark off test intervals on the number line.

 
Below is a graph that marks off the boundary points -6 and 1 and shows the three sections that those points have created on the graph.  Note that open holes were used on those two points since our original inequality does not include where it is equal to 0. 

ad1a3

Note that the two boundary points create three sections on the graph: ad1a4, ad1a5, and ad1a6.


 
 
Step 4: Test a point in each test interval found in step 3 to see which interval(s) is part of the solution set.

 
You can choose ANY point in an interval to represent that interval.  Remember that we are not interested in the actual value that we get, but what SIGN (positive or negative) that we get.

Keep in mind that our inequality is ad12.  Since we are looking for the quadratic expression to be GREATER THAN 0, that means we need our sign to be POSITIVE.

From the interval ad1a4, I choose to use -7 to test this interval:
(I could have used -10, -25, or -10000 as long as it is in the interval)


 
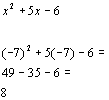
ad1a15

*Chose -7 from 1st interval to plug in for x 

 
Since 8 is positive and we are looking for values that cause our quadratic expression to be greater than 0 (positive), ad1a4 would be part of the solution.

 
 
From the interval ad1a5, I choose to use 0 to test this interval.
(I could have used -5, -4, or -3 as long as it is in the interval)

 
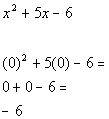
ad1a8

*Chose 0 from 2nd interval to plug in for x 

 


 
Since -6 is negative and we are looking for values that cause our expression to be greater than 0 (positive), ad1a5 would not be part of the solution.

 
 
From the interval ad1a6, I choose to use 2 to test this interval.
(I could have used 10, 25, or 10000 as long as it is in the interval)

 
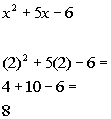
ad1a9

*Chose 2 from 3rd interval to plug in for x 

 


 
Since 8 is positive and we are looking for values that cause our quadratic expression to be greater than 0 (positive), ad1a6 would be part of the solution.

 
 
Step 5: Write the solution set and graph.

 
Interval notation: ad1a10

Graph: 
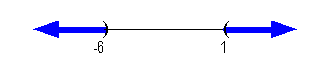
ada11

*Open intervals indicating all values less than -6 or greater than 1

*Visual showing all numbers less than -6 or greater than 1
 


 
(return to problem 1a)


 

 

checkAnswer/Discussion to 1b

problem 1b

I used the test-point method, but you could also use the sign graph of factors method.

 
Step 1: Write the quadratic inequality in standard form.

 
This quadratic inequality is already in standard form.

 
 
Step 2: Solve the quadratic equation, quadratic equation, to get the boundary point(s).

 

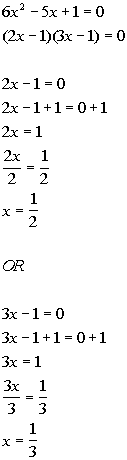
ad1b1

*Factor

*Set 1st factor = 0 and solve
 
 
 
 
 
 
 
 
 
 

*Set 2nd factor = 0 and solve
 
 
 
 

 


 
1/3 and 1/2 are boundary points.

 
Step 3: Use the boundary point(s) found in step 2 to mark off test intervals on the number line.

 
Below is a graph that marks off the boundary points, 1/3 and 1/2, and shows the three sections that those points have created on the graph.  Note that closed holes were used on those two points since our original inequality includes where it is equal to 0. 

adab2

Note that the two boundary points create three sections on the graph: ad1b3, ad1b4 , and ad1b5.


 
 
Step 4: Test a point in each test interval found in step 3 to see which interval(s) is part of the solution set.

 
You can choose ANY point in an interval to represent that interval.  Remember that we are not interested in the actual value that we get, but what SIGN (positive or negative) that we get.

Keep in mind that our original problem is problem 1b.  Since we are looking for the quadratic expression to be LESS THAN OR EQUAL TO 0, that means we need our sign to be NEGATIVE (OR 0).

From the interval ad1b3, I choose to use 0 to test this interval:
(I could have used -10, -25, or -10000 as long as it is in the interval)


 
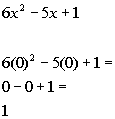
ad1b6

*Chose 0 from 1st interval to plug in for x 

 


 
Since 1 is positive and we are looking for values that cause our quadratic expression to be less than or equal to 0 (negative or 0), ad1b3would not be part of the solution.

 
 
From the interval ad1b4, I choose to use 2/5 to test this interval.
(I could have used 5/12 or 3/8 as long as it is in the interval)

 
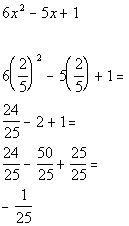
ad1b7

 

*Chose 2/5 from 2nd interval to plug in for x 
 
 
 
 
 
 
 

 


 
Since -1/25 is negative and we are looking for values that cause our expression to be less than or equal to  0 (negative or 0), ad1b4 would be part of the solution.

 
 
From the interval ad1b5, I choose 1 to use  to test this interval.
(I could have used 10, 25, or 10000 as long as it is in the interval)

 
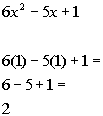
ad1b8

*Chose 1 from 3rd interval to plug in for x 

 


 
Since 2 is positive and we are looking for values that cause our quadratic expression to be less than or equal to 0 (negative or 0), ad1b5 would not be part of the solution.

 
 
Step 5: Write the solution set and graph.

 
Interval notation: ad1b4

Graph: 
ad1b9

*Closed interval indicating all values between 1/3 and 1/2, inclusive

*Visual showing all numbers between 1/3 and 1/2, inclusive

 


   
(return to problem 1b)


 

buffalo top  

WTAMU > Virtual Math Lab > College Algebra > Tutorial 23A: Quadratic Inequalities


Last revised on Dec. 30, 2009 by Kim Seward.
All contents copyright (C) 2002 - 2010, WTAMU and Kim Seward. All rights reserved.