College Algebra
Tutorial 23A: Quadratic Inequalities
WTAMU > Virtual Math Lab > College Algebra
 Learning Objectives Learning Objectives
After completing this tutorial, you should be able to:
-
Solve quadratic inequalities using a sign graph of
factors.
-
Solve quadratic inequalities using the test-point
method.
|
 Introduction Introduction
In this tutorial we will be looking at solving
quadratic inequalities using two different methods. We will be
revisiting solving quadratic
equations to help solve the quadratic inequalities. If you need a
review on solving quadratic equations, feel free to go to Tutorial
17: Quadratic Equations. I think we are ready to
start. |
 Tutorial Tutorial
In other words, a quadratic inequality is in standard
form when the
inequality is set to 0.
Just like in a quadratic equation, the degree of the
polynomial expression
is two. |
Solving
Quadratic Inequalities
Using a Sign Graph of the Factors
|
This
method of solving quadratic inequalities only works if the quadratic
factors. If it doesn't factor then you will need to use the test-point method shown later on this page.
|
Step 1: Write the quadratic
inequality in standard form. |
It is VERY important that one side of the inequality is
0.
0 is our magic number. It is the only number that
separates the
negatives from the positives. If an expression is greater than 0,
then there is no doubt that its sign is positive. Likewise, if it
is less than 0, its sign is negative. You can not say this about
any other number. Since we are working with inequalities, this
idea
will come in handy. With this technique we will be looking at the
sign of a number to determine if it is a solution or not. |
Step 2: Solve the quadratic
equation,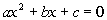 ,
by factoring to get
the boundary point(s). ,
by factoring to get
the boundary point(s). |
The boundary point(s) will mark off where the quadratic
expression
is equal to 0. This is like the cross over point. 0 is
neither
positive or negative.
If you need a review on how to solve a quadratic
equation, feel free
to go to Tutorial 17: Quadratic
Equations.
As mentioned above, this method of
solving quadratic inequalities only works if the quadratic
factors. If
it doesn't factor then you will need to use the test-point
method shown later on this page. |
Step 3: Use the boundary points found in Step 2 to mark off test intervals on
the number line and list all of the factors found in Step 2. |
The boundary point(s) on the number will create test
intervals. |
Step 4: Find the sign of every factor in every interval.
|
You can choose ANY value in an interval to plug into
each factor. Whatever the sign of the factor is with that value
gives you the sign you need for that factor in that interval.
Make sure that you find the sign of every factor in every interval.
Since the inequality will be set to 0, we are not
interested in
the actual value that we get when we plug in our test points, but what
SIGN (positive or negative) that we get. |
Step 5: Using the signs found in Step 4, determine the sign of the overall
quadratic function in each interval.
|
Since the inequality will be set to 0, we are not
interested in
the actual value that we get when we plug in our test points, but what
SIGN (positive or negative) that we get.
When you look at the signs of your factors in each
interval, keep in mind that they represent a product of the factors
that make up your overall quadratic function.
You determine the sign
of the overall quadratic function by using basic multiplication sign
rules:
If the quadratic expression is
less than or
less than or equal to 0, then we are interested in values that cause
the
quadratic expression to be negative.
If the quadratic expression is
greater than
or greater than or equal to 0, then we are interested in values that
cause
our quadratic expression to be positive. |
Step 6: Write the solution
set and graph. |
 Example
1: Solve using a sign graph of factors, write
your answer in interval
notation
and graph the solution set: Example
1: Solve using a sign graph of factors, write
your answer in interval
notation
and graph the solution set: 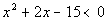 . .
 View a video of this example View a video of this example
|
This quadratic inequality is already in standard form. |
|
*Factor
*Set 1st factor = 0 and solve
*Set 2nd factor = 0 and solve
|
-5 and 3 are boundary points. |
Below is a graph that marks off the boundary points -5
and 3 and shows
the three sections that those points have created on the graph.
Note
that open holes were used on those two points since our original
inequality
did not include where it is equal to 0.
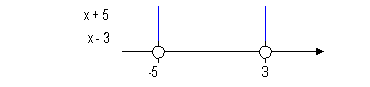
Note that the two boundary points create three sections
on the graph: 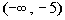 , , 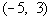 , and , and 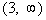 . . |
You can choose ANY point in an interval to represent
that interval.
Remember that we are not interested in the actual value that we get,
but
what SIGN (positive or negative) that we get.
If we chose a number in the first interval, 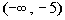 , like -6 , like -6 (I could have used -10, -25, or -10000 as long as it is in the
interval), it would make both factors negative:
-6 + 5 = -1 and -6
- 3 = -9
If we chose a number in the second
interval, 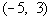 , like 0 (I
could have used -4, -1, or 2 as long as it is in the interval), it
would make x + 5
positive and x - 3
negative:
0 + 5 = 5 and 0 - 3 = -3
If we chose a number in the third
interval, 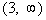 , like
4 (I could have used 10, 25, or
10000 as long as it is in the interval), it would make both factors
positive:
4 + 5 = 9 and 4 - 3
= 1
|
In the first interval, 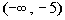 , , we have a
negative times a negative, so the sign of the quadratic in that
interval is positive.
In the second interval, 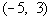 , we have a positive times a negative, so
the sign of the quadratic in that interval is negative.
In the third
interval, 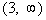 , we
have two positives, so the
sign of the quadratic in that interval is positive.
Keep in mind that our original problem is 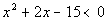 .
Since we are looking for the quadratic expression to be LESS
THAN 0, that means we need our sign to be NEGATIVE.
It looks like the only interval that this quadratic is negative is the second interval, 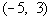 .
|
Interval notation: 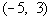
Graph:
 |
*Open interval indicating all
values between
-5 and 3
*Visual showing all numbers
between -5 and
3 on the number line
|
 Example
2: Example
2: Solve using a sign graph of factors, write
your answer in interval
notation
and graph the solution set: 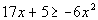 .
 View a video of this example View a video of this example
|
|
*Inv. of sub. 6x squared is add. 6x squared
|
|
*Factor
*Set 1st factor = 0 and solve
*Set 2nd factor = 0 and solve
|
-5/2 and -1/3 are boundary points. |
Below is a graph that marks off the boundary points
-5/2 and -1/3 and
shows the three sections that those points have created on the
graph.
Note that closed holes were used on those two points since our original
inequality includes where it is equal to 0.
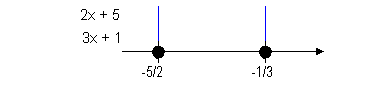
Note that the two boundary points create three sections
on the graph: 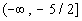 , , 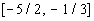 ,
and ,
and 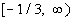 . . |
You can choose ANY point in an interval to represent
that interval.
Remember that we are not interested in the actual value that we get,
but
what SIGN (positive or negative) that we get.
If we chose a number in the first interval, 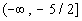 , like -4 , like -4 (I could have used -10, -25, or -10000 as long as it is in the
interval), it would make both factors
negative:
2(-4) + 5 = -3 and
3(-4) + 1 = -11
If we chose a number in the second
interval, 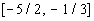 , like
-1 (I could have used -2, -3/2, or -1/2 as long as it is in the interval),
it would make 2x + 5 positive and 3x + 1 negative:
2(-1) + 5 = 3 and 3(-1) +
1 = -2
If we chose a number in the third
interval, 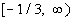 , like 0 (I could have used 10, 25, or
10000 as long as it is in the interval), it would make both factors positive:
2(0) + 5 = 5 and
3(0) + 1 = 1
|
In the first interval, 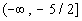 , , we
have a negative times a
negative, so the sign of the quadratic in that interval is positive.
In the second
interval, 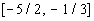 , we have a positive times a negative, so
the sign of the quadratic in that interval is negative.
In the third
interval, 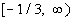 , we have two positives, so the
sign of the quadratic in that interval is positive.
Keep in mind that our inequality is 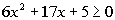 .
Since we are looking for the quadratic expression to be GREATER
THAN OR EQUAL TO 0, that means we need our sign to be POSITIVE
(OR O).
It looks like there are two intervals where the quadratic is positive , the first, 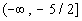 , and the
third, , and the
third, 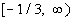 .
|
Interval notation: 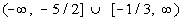
Graph:
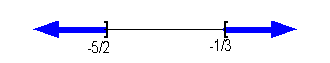 |
*Closed intervals indicating
all values less
than or equal to -5/2 or greater than or equal to -1/3
*Visual showing all numbers
less than or equal
to -5/2 or greater than or equal to -1/3
|
Solving
Quadratic Inequalities
Using the Test-Point Method
|
The
test-point method for solving quadratic inequalities works for any
quadratic that has a real number solution, whether it factors or not.
|
Step 1: Write the quadratic
inequality in standard form. |
It is VERY important that one side of the inequality is
0.
0 is our magic number. It is the only number that
separates the
negatives from the positives. If an expression is greater than 0,
then there is no doubt that its sign is positive. Likewise, if it
is less than 0, its sign is negative. You can not say this about
any other number. Since we are working with inequalities, this
idea
will come in handy. With this technique we will be looking at the
sign of a number to determine if it is a solution or not. |
Step 2: Solve the quadratic
equation,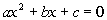 ,
to get
the boundary point(s). ,
to get
the boundary point(s). |
The boundary point(s) will mark off where the quadratic
expression
is equal to 0. This is like the cross over point. 0 is
neither
positive or negative.
If you need a review on how to solve a quadratic
equation, feel free
to go to Tutorial
17: Quadratic
Equations. |
Step 3: Use the boundary
point(s) found in step 2 to mark off test intervals on the number line. |
The boundary point(s) on the number will create test
intervals. |
Step 4: Test a point
in each test interval found in step 3 to see which interval(s) is part
of the solution set. |
You can choose ANY point in an interval to represent
it. You
need to make sure that you test one point from each interval.
Sometimes
more than one interval can be part of the solution set.
Since the inequality will be set to 0, we are not
interested in
the actual value that we get when we plug in our test points, but what
SIGN (positive or negative) that we get.
If the quadratic expression is
less than or
less than or equal to 0, then we are interested in values that cause
the
quadratic expression to be negative.
If the quadratic expression is
greater than
or greater than or equal to 0, then we are interested in values that
cause
our quadratic expression to be positive. |
Step 5: Write the solution
set and graph. |
 Example
3: Example
3: Solve using the test-point method,
write your answer in interval
notation
and graph the solution set: 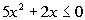 .
 View a video of this example View a video of this example
|
This quadratic inequality is already in standard form. |
|
*Factor
*Set 1st factor = 0 and solve
*Set 2nd factor = 0 and solve
|
-2/5 and 0 are boundary points. |
Below is a graph that marks off the boundary points
-2/5 and 0 and
shows the three sections that those points have created on the
graph.
Note that closed holes were used on those two points since our original
inequality includes where it is equal to 0.

Note that the two boundary points create three sections
on the graph: 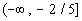 , , 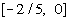 , and , and 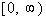 . . |
You can choose ANY point in an interval to represent
that interval.
Remember that we are not interested in the actual value that we get,
but
what SIGN (positive or negative) that we get.
Keep in mind that our original problem is 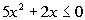 .
Since we are looking for the quadratic expression to be LESS
THAN OR EQUAL TO 0, that means we need our sign to be NEGATIVE
(OR 0). .
Since we are looking for the quadratic expression to be LESS
THAN OR EQUAL TO 0, that means we need our sign to be NEGATIVE
(OR 0).
From the interval 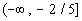 ,
I choose to use -1 to test this interval: ,
I choose to use -1 to test this interval:
(I could have used -10, -25, or -10000 as long as it is in the interval) |
|
*Chose -1 from 1st interval to
plug in for x
|
Since 3 is positive and we are looking for values
that cause our
quadratic expression to be less than or equal to 0 (negative or
0), 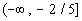 would
not be part of the solution. would
not be part of the solution. |
From the interval 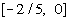 ,
I choose to use -1/5 to test this interval. ,
I choose to use -1/5 to test this interval.
(I could have used -1/6, -1/7, or -1/8 as long as it is in the interval) |
|
*Chose -1/5 from 2nd interval
to plug in for x
|
Since -1/5 is negative and we are looking for values
that cause
our expression to be less than or equal to 0 (negative or
0), 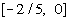 would be part of the solution. would be part of the solution. |
From the interval 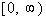 ,
I choose 1 to use to test this interval. ,
I choose 1 to use to test this interval.
(I could have used 10, 25, or 10000 as long as it is in the interval) |
|
*Chose 1 from 3rd interval to
plug in for x
|
Since 7 is positive and we are looking for values
that cause our
quadratic expression to be less than or equal to 0 (negative or
0), 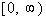 would
not be part of the solution. would
not be part of the solution. |
Interval notation: 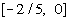
Graph:
 |
*Closed interval indicating
all values between
-2/5 and 0, inclusive
*Visual showing all numbers
between -2/5 and
0, inclusive
|
 Example 4: Example 4: Solve using the test-point method,
write your answer in interval
notation
and graph the solution set: 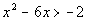 .
 View a video of this example View a video of this example
|
|
*Inv. of sub. 2 is add. 2
|
Since 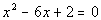 cannot be solved by
factoring, how can we find the solution?
How about using the quadratic formula?
|
|
*Identify a, b, and c
*Quadratic formula
*Plug in values for a, b, and c into formula
*Simplify
|
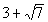 and and 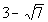 are boundary points. are boundary points. |
Below is a graph that marks off the boundary points 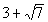 and 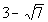 and
shows the three sections that those points have created on the
graph.
Note that open holes were used on those two points since our original
inequality does not include where it is equal to 0.
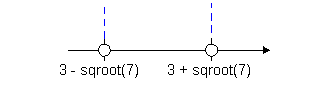
Note that the two boundary points create three sections
on the graph: 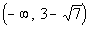 , , 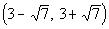 , and , and 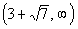 . . |
You can choose ANY point in an interval to represent
that interval.
Remember that we are not interested in the actual value that we get,
but
what SIGN (positive or negative) that we get.
Keep in mind that our original problem is 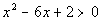 .
Since we are looking for the quadratic expression to be GREATER
THAN 0, that means we need our sign to be POSITIVE. .
Since we are looking for the quadratic expression to be GREATER
THAN 0, that means we need our sign to be POSITIVE.
From the interval 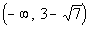 ,
I choose to use 0 to test this interval: ,
I choose to use 0 to test this interval:
(I could have used -10, -25, or -10000 as long as it is in the interval)
Note that 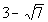 is approximately .35. is approximately .35.
|
|
*Chose 0 from 1st interval to
plug in for x
|
Since 2 is positive and we are looking for values
that cause our
quadratic expression to be greater than 0, 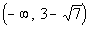 would be
part of the solution. would be
part of the solution. |
From the interval 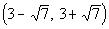 ,
I choose to use 1 to test this interval. ,
I choose to use 1 to test this interval.
(I could have used 2, 3, or 5 as long as it is in the interval)
Note that 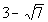 is approximately
.35 and 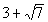 is approximately
5.65.
|
|
*Chose 1 from 2nd interval
to plug in for x
|
Since -3 is negative and we are looking for values
that cause
our expression to be greater than 0, 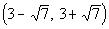 would not be part of the solution. would not be part of the solution. |
From the interval 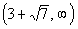 ,
I choose 6 to use to test this interval. ,
I choose 6 to use to test this interval.
(I could have used 10, 25, or 10000 as long as it is in the interval)
Note that 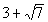 is approximately
5.65.
|
|
*Chose 6 from 3rd interval to
plug in for x
|
Since 2 is positive and we are looking for values
that cause our
quadratic expression to be greater than 0, 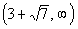 would be
part of the solution. would be
part of the solution. |
 Practice Problems Practice Problems
These are practice problems to help bring you to the
next level.
It will allow you to check and see if you have an understanding of
these
types of problems. Math works just like
anything
else, if you want to get good at it, then you need to practice
it.
Even the best athletes and musicians had help along the way and lots of
practice, practice, practice, to get good at their sport or instrument.
In fact there is no such thing as too much practice. To get the most out of these, you should work the
problem out on
your own and then check your answer by clicking on the link for the
answer/discussion
for that problem. At the link you will find the answer
as well as any steps that went into finding that answer. |
 Practice
Problems 1a - 1b: Solve (using any method), write
your answer in
interval notation
and graph the solution set. Practice
Problems 1a - 1b: Solve (using any method), write
your answer in
interval notation
and graph the solution set.
 Need Extra Help on these Topics? Need Extra Help on these Topics?

Videos at this site were created and produced by Kim Seward and Virginia Williams Trice.
Last revised on Dec. 30, 2009 by Kim Seward.
All contents copyright (C) 2002 - 2010, WTAMU and Kim Seward.
All rights reserved.
|
|


