Beginning Algebra
Answer/Discussion to Practice Problems
Tutorial 34: Central Tendencies

WTAMU > Virtual Math Lab > Beginning Algebra > Tutorial 34: Central Tendencies

Answer/Discussion to 1a
The number of cd's sold by Dave's Discs for the last 6 days are given in the table:

Day	Day 1	Day 2	Day 3	Day 4	Day 5	Day 6
CD's	15	10	10	10	18	15

The mean is the average of the number of discs sold.

So we need to sum up all of the CD's sold and then divide by 6, since there are 6 days:

*(sum of cd's sold)/(# of days)

The mean is 13.

The median is the middle value.

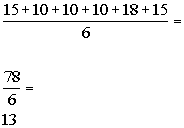
We need to list the numbers in numeric order:
10, 10, 10, 15, 15, 18

If we pick 10 (the third one) for our median we have two values below it and three above it. If we pick 15 (the first one) for our median then we have three values below it and two above it. So neither of those values are the median. This does not mean we don't have a median.

Note how there is an even number of values listed. If that is the case, we need to draw a line down the middle of the list and take the mean of the two numbers next to that line.

10, 10, 10 | 15, 15, 18

The mean of 10 and 15 is

*Find number exactly in the middle of 10 and 15

12.5 is the median. It is the value that is right smack dab in the middle of this list of values.

The mode is the value that occurs the most often.

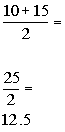
It helps to list the numbers in order to find the mode.
10, 10, 10, 15, 15, 18

Note how 10 occurs three times, which is the value that occurs the most.

10 is the mode.

(return to problem 1a)

Answer/Discussion to 2a
A student received scores of 92, 83, and 71 on three quizzes. If tests count twice as much as quizzes, what is the lowest score that the student can get on the next test to achieve a mean of at least 80?

Keep in mind that the test score counts twice instead of of time. So when we set this up we need to make sure that we notate that properly.

*(sum of scores)/(# of scores) = mean
*Need 2 x's since tests count twice

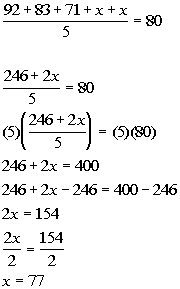
*Solve for x (missing test)

*Inverse of div. by 5 is mult. by 5

*Inverse of add 246 is sub. 246

The student would have to score a 77 on the next test to have a mean of 80.

(return to problem 2a)

Answer/Discussion to 3a
Find the range and standard deviation of the list of scores that were made by a football team during a season:
7, 21, 21, 17, 17, 14, 7, 0

I don't know about you, but I find it easier to work with a group of numbers like this when they are in chronological order. Let's put them in order from lowest to highest: 0, 7, 7, 14, 17, 17, 21, 21.

Let's find the range. What do you think it is?

Looking at the difference between the largest value, which is 21 and the smallest value, which is 0, it looks like the range is 21.

Now lets tackle the standard deviation.

Step 1: Find the mean of the values of the data set.

So we need to sum up all of the values and then divide by 8, since there are 8 numbers:

*(sum of values)/(# of values)

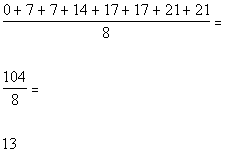
*Add numerator

*Divide by 8

Step 2: Find the difference between the mean and each separate value of the data set,
AND
Step 3: Square each difference found in step 2,
AND
Step 4: Add up all of the squared values found in step 3.

x	x - 13
0	-13	169
7	-6	36
7	-6	36
14	1	1
17	4	16
17	4	16
21	8	64
21	8	64
	SUM:	402

Step 5: Divide the sum found in step 4 by the number of data values in the set
AND
Step 6: Find the nonnegative square root of the quotient found in step 5.

*Square root of [(sum of diff. squared)/(# of values)]

The standard deviation is approximately 7.089.

(return to problem 3a)

Answer/Discussion to 4a

Find the mean of the frequency distribution.

x	f
9	3
10	5
15	4
20	10
Total	22

As requested, I'm going to use the frequency distribution to set up my mean formula. Instead repeating numbers in my sum, I'm going to indicate a repetition by taking that value times the number of times it occurs in the list. For example, 20 occurs 10 times. Instead of writing it out 10 times in my sum, I will find 20(10) which is the equivalent.

*(sum of scores)/(# of scores)

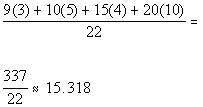
*calculate numerator
*divide

(return to problem 4a)

WTAMU > Virtual Math Lab >Beginning Algebra >Tutorial 34: Central Tendencies