

![]() Learning Objectives
Learning Objectives
![]() Introduction
Introduction
![]() Tutorial
Tutorial
![]()
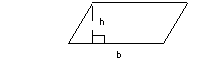
Keep in mind that a rectangle and square are two special types of parallelograms, and would follow this same formula.
So what would be the area of the following parallelogram be?
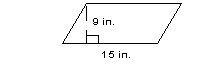
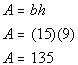
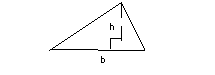
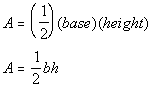
So what would be the area of the following triangle?
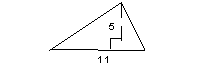
Area and Circumference of a
Circle
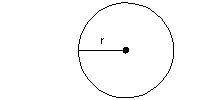
Area:
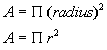
Circumference:
![]()
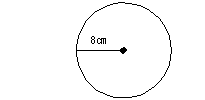
So what would be the area and circumference of the following circle?
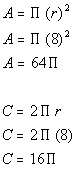
*Circumference
*radius = 8
*multiply
Surface Area and Volume of a
Rectangular Solid
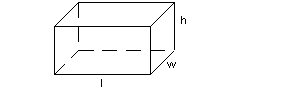
Surface Area:
![]()
Volume:
![]()
So what would be the surface area and volume of the following rectangular solid?
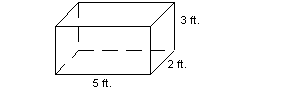
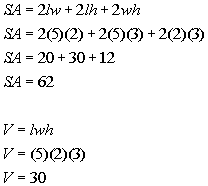
*Volume
*length = 5, width = 2 and height
= 3
*multiply
The volume is 30 cubic feet.
Surface Area and Volume of a
Sphere

Surface Area:
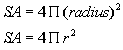
Volume:
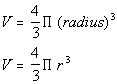
So what would be the surface area and volume of the following sphere?
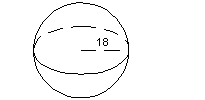
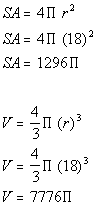
*Volume
*radius = 18
*multiply
The volume is 7776 pi cubic units.
Surface Area and Volume of a
Right Circular Cylinder
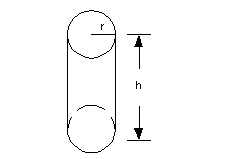
Surface Area:
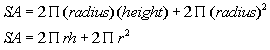
Volume:
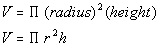
So what would be the surface area and volume of the following right circular cylinder?
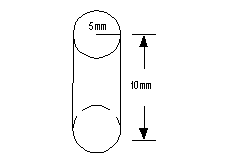
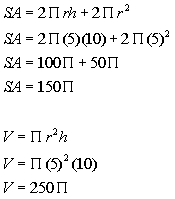
*Volume
*radius = 5 and height = 10
*multiply
The volume is 250 pi cubic millimeters.
Even though there is more than one variable in a
formula, you solve
for a specific variable using the
exact same steps that you do with an equation in one variable, as shown
in Tutorial 14: Solving Linear Equations (Putting it all together).
It is really easy to get overwhelmed when there is more than one variable involved. Sometimes your head feels like it is spinning when you see all of those variables. Isn’t math suppose to be about numbers? Well, just remember that a variable represents a number, so if you need to move it to the other side of the equation you use inverse operations, just like you would do with a number.
 Example
1: Solve the equation
Example
1: Solve the equation In this problem, we need to solve for L. This means we need to get L on one side and EVERYTHING ELSE on the other side using inverse operations.
Let’s solve this formula for L:
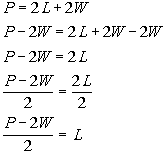
*Inverse of mult. by 2 is div.
by 2
*Formula solved for L
 Example
2: Solve the equation
Example
2: Solve the equation In this problem, we need to solve for r. This means we need to get r on one side and EVERYTHING ELSE on the other side using inverse operations.
Let’s solve this formula for r:
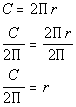
*Inverse of mult. by 2pi is div. by 2pi
*Formula solved for r
 Example
3: Solve the equation
Example
3: Solve the equation In this problem, we need to solve for y. This means we need to get y on one side and EVERYTHING ELSE on the other side using inverse operations.
Let’s solve this formula for y:
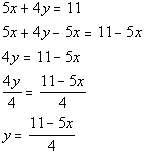
*Inverse of mult. by 4 is div. by 4
*Formula solved for y
 Example
4: Solve the equation
Example
4: Solve the equation In this problem, we need to solve for h. This means we need to get h on one side and EVERYTHING ELSE on the other side using inverse operations.
Let’s solve this formula for h:
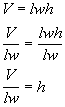
*Formula solved for h
Sometimes you need to do a little figuring. You may need to add, subtract, or take a fraction of the formula(s) you came up with in step 2.
 Example
5: One bag of fertilizer will cover 500 square
feet
of lawn. Your rectangular lawn is 70 feet by 50 feet. How
many
bags of fertilizer will you need to cover it?
Example
5: One bag of fertilizer will cover 500 square
feet
of lawn. Your rectangular lawn is 70 feet by 50 feet. How
many
bags of fertilizer will you need to cover it?Since we are needing to find the area
of a rectangle,
we can use this formula: ![]()
The variables in this formula represent the following:
A = Area of a rectangle
L = length
W = width
Plugging the values into the formula we get:
![]()
7 bags of fertilizer.
 Example
6: The diameter of a beach ball was found to be
18 inches. What is the volume of this beach ball?
Example
6: The diameter of a beach ball was found to be
18 inches. What is the volume of this beach ball?Since we are looking for the volume of a sphere, we can use this formula:
![]()
The variables in this formula represent the following:
V = volume of a sphere
r = radius
![]()
Plugging the values into the formula we get:
![]()
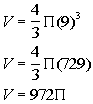
*Multiply
The volume of the beach ball is ![]() cubic
inches.
cubic
inches.
 Example
7: A ramp 13 feet long is leaning against a
raised
platform which is 5 feet above the ground. What is the distance
from
the ramp’s contact point with the ground and the base of the platform?
Example
7: A ramp 13 feet long is leaning against a
raised
platform which is 5 feet above the ground. What is the distance
from
the ramp’s contact point with the ground and the base of the platform? 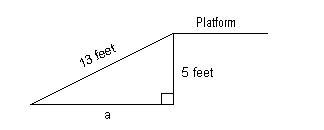
Since we are looking for the side of a right triangle, we can use the Pythagorean formula:
![]()
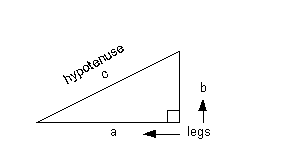
The variables in this formula represent the following:
a and b = legs
of the right triangle
c = hypotenuse of the right
triangle
![]()
Plugging the values into the formula we get:
![]()
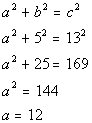
*Subtract 25 from both sides
*What squared gives you 144?
The distance from the ramp’s contact point with the ground and the base of the platform is 12 feet.
 Example
8: A cylindrical pedestal for a statue is to
have
a height of 5 feet and a diameter of 2 feet. The pedestal’s base
is to be a rectangular solid that is 9 feet long, 4 feet wide, and 2
feet
thick. What volume of cement is needed to construct the pedestal
and its base?
Example
8: A cylindrical pedestal for a statue is to
have
a height of 5 feet and a diameter of 2 feet. The pedestal’s base
is to be a rectangular solid that is 9 feet long, 4 feet wide, and 2
feet
thick. What volume of cement is needed to construct the pedestal
and its base? Since part of the problem is looking for the volume of a cylinder, we can use the formula :
![]()
The variables in this formula represent the following:
![]() =
volume of the
cylinder
=
volume of the
cylinder
r = radius
h = height
Since part of the problem is looking for the volume of a rectangular solid, we can use also use the formula:
![]()
The variables in this formula represent the following:
![]() =
Volume of the
rectangular solid
=
Volume of the
rectangular solid
l = length
w = width
h = height
l = 9
w = 4
h (of rectangular solid)= 2
If we take the volume of the cylinder and add it to the volume of the rectangular solid, then we will have the volume that we are looking for:
![]()
Plugging the values into the formula we get:
![]()
The volume of the beach ball is ![]() cubic inches.
cubic inches.
 Example
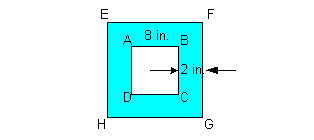
9: Using the figure shown, find the area in
square
feet of the middle region in the square?
Example
9: Using the figure shown, find the area in
square
feet of the middle region in the square? 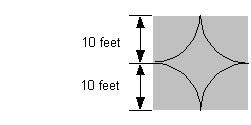
Since part of the problem involves the area of a square, we can use the formula :
The variables in this formula represent the following:
![]() =
area of square
=
area of square
s = side
Since part of the problem involves the area of a circle, we can use also use the formula:
![]()
The variables in this formula represent the following:
![]() =
area of the four
quarter circle corners (four quarters = 1 whole circle)
=
area of the four
quarter circle corners (four quarters = 1 whole circle)
r = radius
If we take the area of the square and subtract out the area of the four quarter circles (whole circle) we will have the area of the middle region of the given figure above:
![]()
Plugging the values into the formula we get:
![]()
The area of the middle region is ![]() square
feet.
square
feet.
 Example
10: A dome is hemispherical in shape with a
radius
of 16 meters and is built using 8 equal sections. What formula
would
describe the surface area of each section?
Example
10: A dome is hemispherical in shape with a
radius
of 16 meters and is built using 8 equal sections. What formula
would
describe the surface area of each section?Since we are looking for the surface area of 1/8 of a hemisphere (half of a sphere), we can use the formula :
![]()
The variables in this formula represent the following:
SA = surface area
r = radius
![]()
Plugging 16 in for r we get:
![]()
Simplifying the expression we get:
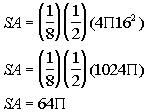
The surface area of one section is ![]() square
meters.
square
meters.
![]() Practice Problems
Practice Problems
To get the most out of these, you should work the problem out on your own and then check your answer by clicking on the link for the answer/discussion for that problem. At the link you will find the answer as well as any steps that went into finding that answer.
Practice Problems 1a - 1b: Solve each equation for the specified variable.
Practice Problems 2a - 2c: Solve the following word problems.
![]() Need Extra Help on these Topics?
Need Extra Help on these Topics?
The following are webpages
that can assist
you in the topics that were covered on this page:
http://www.purplemath.com/modules/solvelit.htm
This webpage helps you with solving formulas for a specified variable.
http://www.purplemath.com/modules/perimetr.htm
This webpage involves a
combination of problem
solving ideas which includes problem solving using formulas.
Go to Get Help Outside the Classroom found in Tutorial 1: How to Succeed in a Math Class for some more suggestions.
Last revised on August 3, 2011 by Kim Seward.
All contents copyright (C) 2001 - 2010, WTAMU and Kim Seward. All rights reserved.