Beginning Algebra
Answer/Discussion to
Practice
Problems
on Formulas
 Answer/Discussion
to 1a
 ;
for T |
Do you recognize this formula?
This happens to be the formula for simple interest, where
I
= simple interest, P = principal, R
= annual percentage rate, and T = time
in years.
In this problem we need to solve for
T.
This means we need to get T on one side
and
EVERYTHING ELSE on the other side using inverse operations.
Let’s solve this formula for T:
|
 |
*Inverse of mult. by PR
is div. by PR
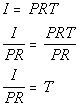
*Formula solved for T
|
Answer/Discussion
to 1b
 ;
for y |
| In this problem we need to solve for y.
This means we need to get y on one side
and
EVERYTHING ELSE on the other side using inverse operations.
Let’s solve this formula for y:
|
 |
*Inverse of add 3x
is sub. 3x
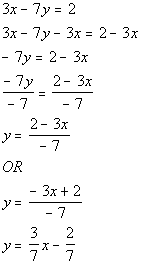
*Inverse of mult. by -7 is div.
by -7
*Formula solved for y
*Divide num. by -7
*Another way to write it
|
Answer/Discussion
to 2a
Sally is training for the Olympics. She likes to run around
a circular track that has a diameter of 60 yards, 20 times during a
workout.
How many yards does she run during her workout? |
Step 1: Identify the type(s)
of figure(s) in
the problem.
AND |
| Step 2: Identify what
formula(s) you need. |
| Make sure that you read the question carefully several
times.
Since we are needing to find the circumference of a
circle,
we can use this formula:
The variables in this formula represent the following:
C = circumference of a
circle
r = radius
|
| Step 3: Put the problem
together. |
In this problem,
C = ? = this is the variable
we are looking
for
r = 30 (radius is half
of the diameter,
so r = 60/2 = 30)
Plugging the values into the formula we get:
|
| First, find the circumference of a circle. |
 |
*Multiply
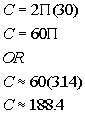
*Replace pi with 3.14 for an
approximate value
|
| For every workout, she runs around the track 20
times. So, we
need to multiply the circumference by 20 to find the number of yards
that
she runs during her workout. |
|
*Multiply
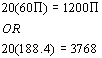
*Multiply using approx. value
|
| FINAL ANSWER:
The number of yards that she runs in a workout
is
1200 or approximately
3768.
|
Answer/Discussion
to 2b
A ramp 5 feet long is leaning against a raised platform which is 4
feet above the ground. What is the distance from the ramp’s
contact
point with the ground and the base of the platform?
|
Step 1: Identify the type(s)
of figure(s) in
the problem.
AND |
| Step 2: Identify what
formula(s) you need. |
| Make sure that you read the question carefully several
times.
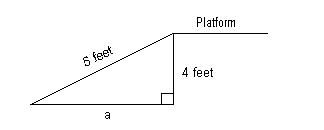
Since we are looking for the side of a right
triangle, we can
use the Pythagorean formula:
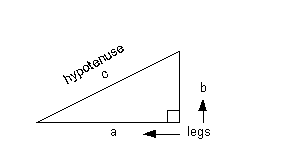
The variables in this formula represent the following:
a and b
= legs
of the right triangle
c = hypotenuse of the right
triangle
|
| Step 3: Put the problem
together. |
In this problem,
a = ? = this is the variable
we are looking
for
b = 4
c = 5
Plugging the values into the formula we get:
|
 |
*Square 4 and 5
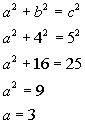
*Subtract 16 from both sides
*What squared gives you 9?
|
| FINAL ANSWER:
The distance from the ramp’s contact point with the
ground and the
base of the platform is 3.
|
Answer/Discussion
to 2c
In the figure, ABCD is a square, with each side of length 8
inches.
The width of the border (shaded portion) between the outer square EFGH
and ABCD is 2 inches. Find the area of the border.
|
Step 1: Identify the type(s)
of figure(s) in
the problem.
AND |
| Step 2: Identify what
formula(s) you need. |
| Make sure that you read the question carefully several
times.
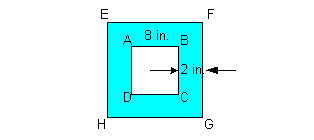
Since part of the problem involves the area of the
big square,
we can use the formula :
The variables in this formula represent the following:
= area of the big
square
s1=
side of the big
square
Since part of the problem involves the area of the
inner square,
we can use also use the formula:
The variables in this formula represent the following:
= area of the inner
square
s2=
side of the inner
square
|
|
| Step 3: Put the problem
together. |
In this problem,
A = ? = this is the variable
we are looking
for
s1 =
8 + 2 + 2 = 12
s2 = 8
If we take the area of the bigger square and subtract
out the area
of the smaller square we will have the area of the border:
Plugging the values into the formula we get:
|
 |
*Square 20 and 10 |
| FINAL ANSWER:
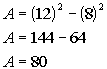
The area of the border is 80 square inches.
|
All contents copyright (C) 2001 - 2008, WTAMU and Kim Seward. All rights reserved.
Last revised on Jan. 10, 2002 by Kim Seward. |
