

![]()
When I'm working with only the boundary line, I will put an equal sign between the two sides to emphasize that we are working on the boundary line. That doesn't mean that I changed the problem. When we put it all together in the end, I will put the inequality back in.
What value is y on the x-intercept?
If you said 0, you are correct.
If you need a review on x-intercepts,
go to Tutorial 22: Intercepts.
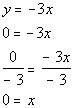
*x-intercept
Since the x-intercept came out to be (0,
0), then it stands to reason that when we put in 0 for x to find the y-intercept, we will get (0,
0).
Let's move on and plug in 1 for x to get a second solution:
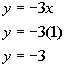
Plug in -1 for x to get a third solution:
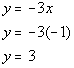
Solutions:
Since the original problem has a >, this means it DOES include the boundary line.
So are we going to draw a solid or a dashed line for this problem?
It looks like it will have to be a solid line.
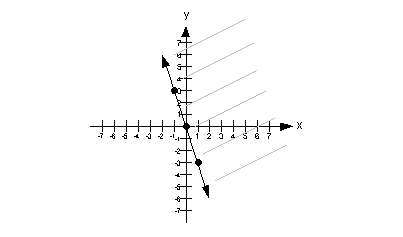
Putting it all together, we get the following boundary line for this problem:
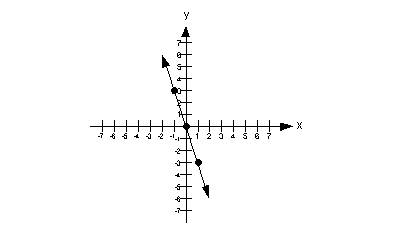
An easy test point would be (1, 1). Note that it is a point that is not on the boundary line. In fact, it is located above the boundary line.
Let's put (1, 1) into the original problem and see what happens:
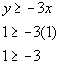
Our solution would lie above the boundary line. This means we will shade in the part that is above it.
Note that the gray lines indicate where you would shade your final answer.
![]()
Do you remember what type of line y = c graphs as?
It comes out to be a horizontal line.
If you need a review
on horizontal lines, go to Tutorial 22: Intercepts
Every y's value on the boundary line would have to be 3.
Solutions:
x
y
(x, y)
0
3
(0, 3)
1
3
(1, 3)
2
3
(2, 3)
So are we going to draw a solid or a dashed line for this problem?
It looks like it will have to be a dashed line.
Putting it all together, we get the following boundary line for this problem:
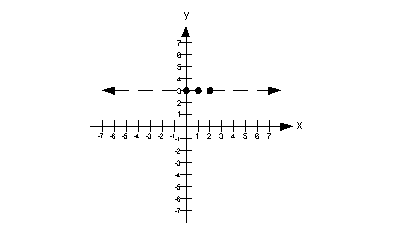
An easy test point would be (0, 0). Note that it is a point that is not on the boundary line. In fact, it is located below the boundary line.
Let's put (0, 0) into the original problem and see what happens:
Our solution would lie below the boundary line. This means we will shade in the part that is below it
Note that the gray lines indicate where you would shade your final answer.
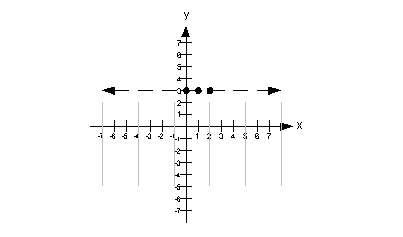
Last revised on July 31, 2011 by Kim Seward.
All contents copyright (C) 2001 - 2011, WTAMU and Kim Seward.
All rights reserved.