College Algebra
Tutorial 62: Compound Interest: Present Value
 Learning Objectives
After completing this tutorial, you should be able to:
- Set up and solve a present value compound interest problem given a finite number of compound periods.
- Set up and solve a present value continuous compound interest problem.
|
Introduction
In this tutorial, we will continue looking at applications of MONEY! In Tutorial 61: Compound Interest: Future Value, we learned how to find the future value given the present value, compound periods, time and nominal rate. In this tutorial, we will be learning how to find the present value of an account that is either compounded for a finite number of times or continuously. Even if you are
not
a business related major, a lot of these applications can be used with
your own finances.
It is to your benefit to step through the examples on the
page with
your calculator to make sure that you understand how to work the
problems.
Let's have some more fun working with money!!!
|
Tutorial
The Negative Key
on the Calculator
|
In this part of the lesson you will notice that our exponent
ends up
negative. I wanted to make sure everyone knew how to enter in a
negative
exponent.
The two main negative keys found on
calculators
are (you will only have one of these):
( ) around the negative:
(-)
|
Plus minus sign:
+/-
|
Check to see if you have one of the two main type of
negative keys
(you won’t have both). If you don’t have one check the
other.
If you don’t see either, look in the reference manual that came with
the
calculator to see which key it is or email me.
The (-) key is most
frequently found
on graphing calculators but can be found on other types of calculators.
On most graphing calculators your negative key
is the ( ) around
the - key, usually found to the left of the enter key:
(-)
(This is one key)(NOT the subtraction key).
So if you have this key let's practice taking 2 raised to the -4
power.
To do this you would type in 2^(-)4 and press your enter or =
key.
If you got .0625, you entered it in correctly. If not, try
again. If you still can't get it either look in your
reference
manual that came with the calculator or email me and I will try yo help
you. |
The +/- key is most
common in business
and scientific calculators, but can be found on other types of
calculators.
On most business and scientific calculators,
the negative key looks
like +/-. So check for this key. If you have this
key let's practice taking 2 raised to the -4 power. In this
situation,
you first type in your base, then you activate your exponent key (as described in Tutorial 61: Compound Interest: Future Value), and then you type in 4 and then press
the +/- key - note how that changes 4 to -4. Now press your
enter or = key. You should have gotten .0625 as your answer. If
not,
try again. If you still can't get it, either look in your
reference
manual that came with the calculator or email me and I will try to help
you.
Be very careful, the
+/- key is pressed
after you put in the number you want to be negative, not before it.
Actually it is a toggle key every time you press it, it changes the
sign
of the number on the screen, So if it was negative and you
pressed
+/-, then it would turn into positive and vice versa. |
|
|
The present value is the principal amount that is invested.
There are certain types of situations that you will know the
amount
that you want for the end result (future value), and based on the
interest
rate you can figure out how much you should currently invest to get the
desired return after a certain time period. |
Present Value
Formula
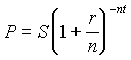
P = present value (or
principal)
S = compound amount (end
value)
r = nominal rate
n = number of compound periods per
year
t = number of years |
Note that some of the letters used in this formula may look
different than
the one in your book.
In some books they use A or Fv instead of S. Just note that this formula is set up to find the present value of an account where the interest is compounded, whether you call it S, A, or Fv.
Also, in some books, an i is used instead of r/n. I like to write the formula out using r/n because it helps to remind us that we need to divide the periodic rate by the number of compound periods per year.
I want to draw your attention to the negative sign in the
exponent.
We are going in reverse - given compound amount (end) and finding the
present
value. Our answer is going to end up being smaller than the given
compound amount.
 Example
1: Find the present value of the given future payment
at the specified interest rate.
$7000 due in 10 years at 7% compounded semiannually. |
|
*7% written in decimal form
*Compounded semiannually - 2 times
per year
*Present value formula
*Plug in values into PV form.
*Calculate number inside ( )
and exponent
*Raise inside of ( ) to the -20th
power
|
This means that our present value (or principal) would
have to be
$3517.96, in order to have an end result of $7000 after 10 years at
7% compounded semiannually. |
Example
2: A trust fund for a child’s education is being set
up
by a single payment so that at the end of 15 years there will be
$24000.
If the fund earns interest at a rate of 8% compounded quarterly, how
much
money should be paid into the fund? |
Looks like we are looking for the present value - we are
needing to
know how much needs to be paid into the fund right now, given the end
result. |
|
*8% written in decimal form
*Compounded quarterly - 4 times per year
*Present value formula
*Plug in values into PV form.
*Calculate number inside ( )
and exponent
*Raise inside of ( ) to the
-60th power
|
So that means we would have to currently put
$7314.77 into
the education fund and after being compounded quarterly at a rate of 8%
for 15 years we should have the desired amount of $24000. Sounds
pretty good - that is letting your money work for you. |
Practice Problems
These are practice problems to help bring you to the next level.
It will allow you to check and see if you have an understanding of these
types of problems. Math works just like anything
else, if you want to get good at it, then you need to practice it.
Even the best athletes and musicians had help along the way and lots of
practice, practice, practice, to get good at their sport or instrument.
In fact there is no such thing as too much practice. To get the most out of these, you should work the problem out on
your own and then check your answer by clicking on the link for the answer/discussion
for that problem. At the link you will find the answer
as well as any steps that went into finding that answer. |
 Practice
Problem 1a: Find the present value of the given future value payment at the
specified
interest rate.
Practice
Problem 2a: Solve the given future value problem.
A trust fund for a 1 year old child is being set up by a
single payment
so at the age of 25 the child will receive $50000. Find how much
the payment is if an interest rate of 5% compounded monthly is
assumed.
(answer/discussion
to 2a) |
Need Extra Help on these Topics?
Last revised on October 8, 2011 by Kim Seward.
All contents copyright (C) 2002 - 2011, WTAMU and Kim Seward. All rights reserved.
|
|
