College Algebra
Tutorial 56: Permutation
 Learning Objectives
After completing this tutorial, you should be able to:
- Use permutations to solve a counting problem
involving order.
|
Introduction
In this tutorial we will be going over
permutations. Permutations
are an off shoot of the Fundamental Counting Principle. If you need a
review
on the Fundamental Counting Principle, feel free to go to Tutorial
55: The Fundamental Counting Principle. Permutations
specifically
count the number of ways a task can be arranged or ordered. I think you
are ready to go off into the wonderful world of permutations, have fun! |
Tutorial
The factorial symbol is the exclamation point: !
So if I wanted to write 7 factorial it would be written
as 7!.
In general, n! = n(n - 1)(n -
2)(n - 3)...(1)
Most, (if not all), of you will have a factorial key
on your calculator.
It looks like this: !
If you have a graphing calculator, it will be hidden
under the MATH
menu screen and then select your Probability screen - there you should
find !
Some calculators don’t have one, so I will show you how
to simplify
the problems in case you don’t have that key on your calculator.
0! Has a special
definition attached
with it. 0! = 1 |
 Example
1: Find 7! |
If you have a ! key on your calculator you simple press
7 and then
! and in some cases you may have to also press your enter or = key.
If you don’t have this key you will have to enter the
definition in
as follows:
7! = (7)(6)(5)(4)(3)(2)(1) = 5040
Either way 7! = 5040. |
We needed to know about factorial because it is used
the formula for
permutation, which is our next topic. |
|
Permutation
An ORDER of arrangements
of r objects,
without repetition, selected from n distinct
objects is called a permutation of n objects
taken r at a time, and is denoted as
|
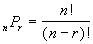
In other words, when you need to count the number of
ways you can
arrange items where ORDER is important, then you can use permutation to
count.
For example, you may want to know how many ways to pick
a 1st, 2nd,
and 3rd place winner from 10 contestants. Since you are arranging
them in order, you could use a permutation to do this. Or if you
were wanting to know how many ways your committee could pick a
president,
a vice president, a secretary, and a treasurer, you could use
permutations. |
Example
2: In how many ways can 8 CD’s be arranged on a
shelf? |
Since we are arranging these CD’s that means order
is important.
So we can use permutations to help us out here.
First we need to find n and r :
n is the number of
CD's we have to choose
from. What do you think n is
in
this problem?
If you said n is
8 you are correct!!!
There are 8 CD's in this problem.
r is the number of
CD’s we are using at
a time. What do you think r is?
If you said r is
8, pat yourself
on the back!! We are arranging all 8 CD's on the shelf. |
Putting this into the permutation formula we get: |
|
*n = 8, r = 8
*0! = 1
*Expand out 8!
|
If you have a factorial key, you can put it in as 8!
divided by
0! and then press enter or =.
If you don't have a factorial key, you can simplify it
as shown above
and then enter it in. It is probably best to simplify it first,
because
in some cases the numbers can get rather large, and it would be
cumbersome
to multiply all those numbers one by one.
Wow, this means there are 40320 different ways to
arrange those 8
CD’s, that’s a lot. |
Example
3: If a softball league has 10 teams, how many
different
end of the season rankings are possible? (Assume no ties). |
Since we are ranking these teams that means order is
important.
So we can use permutations to help us out here.
First we need to find n and r :
n is the number of
teams we have to choose
from. What do you think n is
in
this problem?
If you said n is
10 you are correct!!!
There are 10 teams in this problem.
r is the number of
teams we are ranking
at a time. What do you think r is?
If you said r is
10, pat yourself
on the back!! We are ranking all 10 teams. |
Putting this into the permutation formula we get: |
|
*n = 10, r = 10
*0! = 1
*Expand out 10!
|
If you have a factorial key, you can put it in as
10! divided by
0! and then press enter or =.
If you don't have a factorial key, you can simplify it
as shown above
and then enter it in. It is probably best to simplify it first,
because
in some cases the numbers can get rather large, and it would be
cumbersome
to multiply all those numbers one by one.
Wow, this means there are 3,628,800 different ways to
rank those
10 teams, that’s a lot. |
Example
4: In how many ways can a sorority of 20 members
select
a president, vice president and treasury, assuming that the same person
cannot hold more than one office. |
Since we are choosing offices, which is a way to
rank members, that
means order is important. So we can use permutations to help us
out
here.
First we need to find n and r :
n is the number of
members we have to choose
from. What do you think n is
in
this problem?
If you said n is
20 you are correct!!!
There are 20 members in this problem.
r is the number of
members we are selecting
for offices at a time. What do you think r is?
If you said r is
3, pat yourself
on the back!! There are 3 offices. |
Putting this into the permutation formula we get: |
|
*n = 20, r = 3
*Expand 20! until it gets to
17! ( which is
the ! in den)
*Cancel out 17!'s |
If you have a factorial key, you can put it in as
20! divided by
17! and then press enter or =.
If you don't have a factorial key, you can simplify it
as shown above
and then enter it in. It is probably best to simplify it first,
because
in some cases the numbers can get rather large, and it would be
cumbersome
to multiply all those numbers one by one.
Wow, this means there are 6840 different ways to
select the three
officers, that’s a lot. |
Example
5: How many different arrangements can be made using
two
of the letters of the word TEXAS if no letter is to be used more than
once? |
Since we are arranging letters, this means order is
important.
So we can use permutations to help us out here.
First we need to find n and r :
n is the number of
letters we have to choose
from. What do you think n is
in
this problem?
If you said n is
5 you are correct!!!
There are 5 letters in TEXAS.
r is the number of
letters we are using
at a time. What do you think r is?
If you said r is
2, pat yourself
on the back!! We are using 2 letters at a time. |
Putting this into the permutation formula we get: |
|
*n = 5, r = 2
*Expand 5! until it gets to 3!
( which is the
! in den)
*Cancel out 3!'s |
If you have a factorial key, you can put it in as 5!
divided by
3! and then press enter or =.
If you don't have a factorial key, you can simplify it
as shown above
and then enter it in. It is probably best to simplify it first,
because
in some cases the numbers can get rather large, and it would be
cumbersome
to multiply all those numbers one by one.
This means there are 20 different 2 letter
arrangements. |
Practice Problems
These are practice problems to help bring you to the next level.
It will allow you to check and see if you have an understanding of these
types of problems. Math works just like anything
else, if you want to get good at it, then you need to practice it.
Even the best athletes and musicians had help along the way and lots of
practice, practice, practice, to get good at their sport or instrument.
In fact there is no such thing as too much practice.
To get the most out of these, you should work the problem out on
your own and then check your answer by clicking on the link for the answer/discussion
for that problem. At the link you will find the answer
as well as any steps that went into finding that answer. |
 Practice Problems 1a - 1c: Solve using permutations.
1a. A company issues a questionnaire whereby each
employee must rank
the 5 items with which he or she is most satisfied. The items are
wages, work environment, vacation time, job security, supervisors,
health
insurance, break time, and retirement plan.
The ranking is to be indicated by the numbers 1, 2, 3, 4
and 5, where
1 indicates the item involving the greatest satisfaction and 5 the
least.
In how many ways can an employee answer this questionnaire?
(answer/discussion
to 1a)
|
1b. A key pad lock has 10 different digits, and a
sequence of 5 different
digits must be selected for the lock to open. How many key pad
combinations
are possible?
(answer/discussion
to 1b) |
Need Extra Help on these Topics?
Last revised on May 20, 2011 by Kim Seward.
All contents copyright (C) 2002 - 2011, WTAMU and Kim Seward. All rights reserved.
|
|
