College Algebra
Tutorial 55: Fundamental Counting Principle
 Learning Objectives
After completing this tutorial, you should be able to:
- Use the Fundamental Counting Principle to determine
the number of
outcomes
in a problem.
|
Introduction
In this tutorial we will be going over the Fundamental
Counting Principle.
It will allow us to count the number of ways a task can occur given a
series
of events. Basically you multiply the number of possibilities
each
event of the task can occur. It is like multiplying the
dimensions
of it. I think you are ready to count away. |
Tutorial
Suppose that a task involves a sequence of k choices. Let 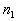 be the number of ways the first stage or event can occur and 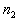 be the number of ways the second stage or event can occur after the
first
stage has occurred. Continuing in this way, let 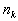 be the number of ways the kth stage or
event
can occur after the first k - 1 stages
or events
have occurred. Then the total number of different ways the
task
can occur is:
|
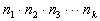
 Example
1: A deli has a lunch special which
consists
of a sandwich, soup, dessert and drink for $4.99. They offer the
following choices: Sandwich: chicken salad, ham, and tuna, and roast
beef
Soup: tomato, chicken noodle, vegetable
Dessert: cookie and pie
Drink: tea, coffee, coke, diet coke and sprite
How many lunch specials are there? |
Let’s use the basic counting principle:
There are 4 stages or events: choosing a sandwich,
choosing a soup,
choosing a dessert and choosing a drink.
There are 4 choices for the sandwich, 3 choices for
the soup, 2 choices
for the dessert and 5 choices for the drink.
Putting that all together we get:
|
Sand.
|
|
Soup
|
|
Dessert
|
|
Drink
|
|
# of lunch specials
|
|
4
|
x
|
3
|
x
|
2
|
x
|
5
|
=
|
120
|
So there are 120 lunch specials possible. |
Example
2: You are taking a test that has five
True/False
questions. If you answer each question with True or False and
leave
none of them blank, in how many ways can you answer the whole test? |
Let’s use the basic counting principle:
There are 5 stages or events: question 1, question 2,
question 3, question
4, and question 5.
There are 2 choices for each question.
Putting that all together we get:
quest. 1
|
|
quest. 2
|
|
quest. 3
|
|
quest. 4
|
|
quest. 5
|
|
# of ways to answer
test
|
|
2
|
x
|
2
|
x
|
2
|
x
|
2
|
x
|
2
|
=
|
32
|
So there are 32 different ways to answer the whole
test. |
|
Example
3: A company places a 6-symbol code on
each
unit of product. The code consists of 4 digits, the first of
which
is the number 5, followed by 2 letters, the first of which is NOT
a vowel. How many different codes are possible? |
Let’s use the basic counting principle:
There are 6 stages or events: digit 1, digit 2, digit 3,
digit 4, letter
1, and letter 2.
In general there are 10 digits: 0, 1, 2, 3, 4, 5, 6, 7,
8, and 9.
The first digit is limited to being the number 5, so there is only one
possibility for that one. There are no restriction on digits 2 -
4, so each one of those has 10 possibilities.
In general, there are 26 letters in the alphabet. The
first letter,
cannot be a vowel (a, e, i, o, u), so that means there are 21 possible
letters that could go there. The second letter has no
restriction,
so there are 26 possibilities for that one.
Putting that all together we get:
|
digit 1
|
|
digit 2
|
|
digit 3
|
|
digit 4
|
|
letter 1
|
|
letter 2
|
|
# of codes
|
|
1
|
x
|
10
|
x
|
10
|
x
|
10
|
x
|
21
|
x
|
26
|
=
|
546000
|
So there are 546000 different 6-symbol codes possible. |
|
Practice Problems
These are practice problems to help bring you to the next level.
It will allow you to check and see if you have an understanding of these
types of problems. Math works just like anything
else, if you want to get good at it, then you need to practice it.
Even the best athletes and musicians had help along the way and lots of
practice, practice, practice, to get good at their sport or instrument.
In fact there is no such thing as too much practice.
To get the most out of these, you should work the problem out on
your own and then check your answer by clicking on the link for the answer/discussion
for that problem. At the link you will find the answer
as well as any steps that went into finding that answer. |
 Practice Problems 1a - 1c: Solve using the counting principle.
1b. Next semester you are going to take one
science class, one
math class, one history class and one english class. According to
the schedule you have 4 different science classes, 3 different math
classes,
2 different history classes, and 3 different English classes to choose
from. Assuming no scheduling conflicts, how many different
four-course
selections can you make?
(answer/discussion
to 1b) |
1c. Six students in a speech class all have to
give there speech
on the same day. One of the students insists on being
first.
If this student’s request is granted, how many different ways are there
to schedule the speeches?
(answer/discussion
to 1c) |
Need Extra Help on these Topics?
Last revised on May 19, 2011 by Kim Seward.
All contents copyright (C) 2002 - 2011, WTAMU and Kim Seward. All rights reserved.
|
|
