College Algebra Tutorial 54


College Algebra
Answer/Discussion to Practice Problems  
Tutorial 54: The Binomial Theorem

WTAMU > Virtual Math Lab > College Algebra > Tutorial 54: The Binomial Theorem


 

checkAnswer/Discussion to 1a

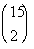
problem 1a
 

Looks like we are going to need to use the definition of a binomial coefficient to help us out on this.
 

Looking at the definition of binomial coefficient, what is n?

If you said 15, you are correct!!!  n is the top number, which in this case is 15.
 

Looking at the definition of binomial coefficient, what is r?

If you said 2, give yourself a pat on the back!!!!   r is the bottom number, which in this case is 2.
 

Putting those values into the definition of a binomial coefficient we get:
 

ad1a

 
 

*n = 15, r = 2
 
 

*Eval. inside ( )

*Expand 15! until it gets to 13!
  which is the larger ! in the den.

*Cancel out 13!'s
 

 
 

If you have a factorial key, you can put it in as 15! divided by 13! divided by 2! and then press enter or =.

If you don't have a factorial key, you can simplify it as shown above and then enter it in.  It is probably best to simplify it first, because in some cases the numbers can get rather large, and it would be cumbersome to multiply all those numbers one by one.

The final answer is 105. 

(return to problem 1a)


 

checkAnswer/Discussion to 1b

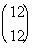
problem 1b
 

Looks like we are going to need to use the definition of a binomial coefficient to help us out on this.
 

Looking at the definition of binomial coefficient, what is n?

If you said 12, you are correct!!!  n is the top number, which in this case is 12.
 

Looking at the definition of binomial coefficient, what is r?

If you said 12, give yourself a pat on the back!!!!   r is the bottom number, which in this case is 12.
 

Putting those values into the definition of a binomial coefficient we get:
 

ad1b
*n = 12, r = 12
 
 

*Eval. inside ( )
*0! = 1
 

*Cancel out 12!'s
 

If you have a factorial key, you can put it in as 12! divided by 0! divided by 12! and then press enter or =.

If you don't have a factorial key, you can simplify it as shown above and then enter it in.  It is probably best to simplify it first, because in some cases the numbers can get rather large, and it would be cumbersome to multiply all those numbers one by one.

The final answer is 1. 

(return to problem 1b)


 

checkAnswer/Discussion to 2a

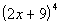
problem 2a
 

Looks like we are going to need to use the Binomial Theorem to help us out on this.

Looking at the Binomial Theorem, what is a?

If you said 2x, you are correct!!! a is the first term of the binomial, which in this case is 2x.
 

Looking at the Binomial Theorem, what is b?

If you said 9, give yourself a pat on the back!!!!   b is the second term of the binomial, which in this case is 9.
 

Looking at the Binomial Theorem, what is n?

If you said 4, give yourself a high five!!!!   n is the exponent on the binomial, which in this case is 4.
 

Putting those values into the Binomial Theorem we get:
 

ad2a1

 
 

*a = 2x, b = 9,n = 4
 
 
 
 
 

*Use definition of binomial coefficient
 

*Eval.  2x's and 9's raised to exponents
 
 
 

*Eval. inside ( )
 
 
 
 

*Expand num. until it gets to
larger ! in the den.
 
 
 

*Cancel out !'s
 
 
 
 

*Simplify
 

If you have a factorial key, you can put in the binomial coefficient part of each term as the (top number)! divided by the (first number in the denominator) ! divided by the (second number in the denominator)! and then press enter or =.

If you don't have a factorial key, you can simplify it as shown above and then enter it in.  It is probably best to simplify it first, because in some cases the numbers can get rather large, and it would be cumbersome to multiply all those numbers one by one.

So our final answer is 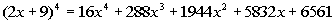ad2a2.

(return to problem 2a)


 

checkAnswer/Discussion to 2b

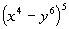
problem 2b
 

Looks like we are going to need to use the Binomial Theorem to help us out on this.

Looking at the Binomial Theorem, what is a?

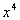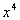If you said ad2b1, you are correct!!! a is the first term of the binomial, which in this case is ad2b1.
 

Looking at the Binomial Theorem, what is b?

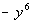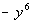If you said ad2b2, give yourself a pat on the back!!!!   b is the second term of the binomial, which in this case is ad2b2.
 

Looking at the Binomial Theorem, what is n?

If you said 5, give yourself a high five!!!!   n is the exponent on the binomial, which in this case is 5.
 

Putting those values into the Binomial Theorem we get:
 

ad2b5

 
 

*a = x^4, b = -y^6, n = 5
 
 
 

*Use definition of binomial coefficient
 

*Eval.  x^4's and -y^6's raised to exponents
 
 
 
 
 

*Eval. inside ( )
 
 
 
 

*Expand num. until it gets to
larger ! in the den.
 
 
 

*Cancel out !'s
 
 
 
 

*Simplify
 

If you have a factorial key, you can put in the binomial coefficient part of each term as the (top number)! divided by the (first number in the denominator) ! divided by the (second number in the denominator)! and then press enter or =.

If you don't have a factorial key, you can simplify it as shown above and then enter it in.  It is probably best to simplify it first, because in some cases the numbers can get rather large, and it would be cumbersome to multiply all those numbers one by one.

So our final answer is 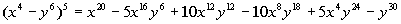ad2b4.

(return to problem 2b)


 

checkAnswer/Discussion to 3a

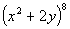problem 3a;  fifth term
 

Looks like we are going to need to use the rth term expansion formula to help us out on this.
 

Looking at the rth term expansion formula, what is n?

If you said 8, you are correct!!!  n is the exponent on your binomial, which in this case is 8.
 

Looking at the rth term expansion formula, what is r?

If you said 5, give your self a pat on the back!!!!   r is the number of the term to be found, which in this case is 5.
 

Looking at the rth term expansion formula, what is a?

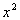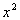If you said example 9d, you are correct!!!  a is the first term of the binomial, which in this case is example 9d.
 

Looking at the rth term expansion formula, what is b?

If you said 2y, give yourself a pat on the back!!!!   b is the second term of the binomial, which in this case is 2y. 
 

Putting those values into the rth term expansion formula we get:
 

ad3a1
*n = 8, r = 5, a = x^2, b = 2y
 
 
 
 
 
 
 

*Use definition of binomial coefficient
 

*Eval. inside ( )
 
 

*Expand 8! until it gets to 4!
which is the larger ! in the den.

*Cancel out !'s
 
 

*Simplify
 
 

If you have a factorial key, you can put the binomial coefficient in as 8! divided by 4! divided by 4! and then press enter or =.

If you don't have a factorial key, you can simplify it as shown above and then enter it in.  It is probably best to simplify it first, because in some cases the numbers can get rather large, and it would be cumbersome to multiply all those numbers one by one.

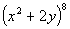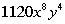This would tell us that the 5th term of the binomial problem 3a would be ad3a2. 

(return to problem 3a)


 

checkAnswer/Discussion to 3b

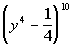problem 3b ;   fourth term
 

Looks like we are going to need to use the rth term expansion formula to help us out on this.
 

Looking at the rth term expansion formula, what is n?

If you said 10, you are correct!!!  n is the exponent on your binomial, which in this case is 10.
 

Looking at the rth term expansion formula, what is r?

If you said 4, give your self a pat on the back!!!!   r is the number of the term to be found, which in this case is 4.
 

Looking at the rth term expansion formula, what is a?

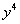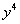If you said ad3b4, you are correct!!!  a is the first term of the binomial, which in this case is ad3b4.
 

Looking at the rth term expansion formula, what is b?

If you said -1/4, give yourself a pat on the back!!!!   b is the second term of the binomial, which in this case is -1/4. 
 

Putting those values into the rth term expansion formula we get:
 

ad3b5
*n = 10, r = 4, a = y^4, b = -1/4
 
 
 
 

*Use definition of binomial coefficient
 
 
 

*Eval. inside ( )
 
 

*Expand 10! until it gets to 7!
which is the larger ! in the den.
 

*Cancel out !'s
 
 

*Simplify
 
 

If you have a factorial key, you can put the binomial coefficient in as 10! divided by 7! divided by 3! and then press enter or =.

If you don't have a factorial key, you can simplify it as shown above and then enter it in.  It is probably best to simplify it first, because in some cases the numbers can get rather large, and it would be cumbersome to multiply all those numbers one by one.

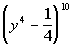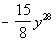This would tell us that the 4th term of the binomial problem 3b would be ad3b6. 

(return to problem 3b)

 

Buffalo top

 
WTAMU > Virtual Math Lab > College Algebra >Tutorial 54: The Binomial Theorem


Last revised on May 16, 2011 by Kim Seward.
All contents copyright (C) 2002 - 2011, WTAMU and Kim Seward. All rights reserved.