College Algebra Tutorial 54


College Algebra
Tutorial 54: The Binomial Theorem

WTAMU > Virtual Math Lab > College Algebra

 

deskLearning Objectives


After completing this tutorial, you should be able to:
  1. Evaluate a factorial.
  2. Find a binomial coefficient.
  3. Use the Binomial Theorem to expand a binomial raised to a power.
  4. Find the rth term of a binomial expansion.




deskIntroduction


In this tutorial we will mainly be going over the Binomial Theorem.  To get to that point I will first be showing you what a factorial is.  This is needed to complete problems in this section.  This will lead us into the concept of finding a binomial coefficient, which incorporates factorials into it's formula.  From there we will put it together into the Binomial Theorem.  This theorem gives us a formula that enables us to find the expansion of a binomial raised to a power, without having to multiply the whole thing out.  This theorem incorporates the binomial coefficient formula.  You will see that everything in this tutorial intertwines.  I think that you are ready to move ahead. 

 

 

desk Tutorial

 
  Factorial
!
 

The factorial symbol is the exclamation point: !

So if I wanted to write 7 factorial it would be written as 7!.

In general, n! = n(n - 1)(n - 2)(n - 3)...(1)

Most, (if not all), of you will have a factorial key on your calculator.  It looks like this: !

If you have a graphing calculator, it will be hidden under the MATH menu screen and then select your Probability screen - there you should find !

Some calculators don't have one, so I will show you how to simplify the problems in case you don't have that key on your calculator.

0!  Has a special definition attached with it.  0! = 1
 
 
 

notebook Example 1: Find 7!

 
If you have a ! key on your calculator you simply press 7 and then ! and in some cases you may have to also press your enter or = key.

If you don't have this key you will have to enter the definition in as follows: 7! = (7)(6)(5)(4)(3)(2)(1) = 5040

Either way 7! = 5040.
 

We needed to know about factorials because it is used in the formula for binomial coefficients, which is our next topic.


  Binomial Coefficient

For nonnegative integers n and r, with n > r,
a binomial coefficient is defined by

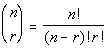
binomial coefficient
 

This formula can be used to find the coefficient of various terms of a binomial that has been expanded.  Believe it or not, it can save you a lot of time if you are needing to know what polynomial you get if you raise a binomial to a large power.  It can be very time consuming and cumbersome to multiply out a binomial that is raised to the 6th, 10th, 20th power, etc... This formula is going to lead us into Binomial Theorem which gives us a shortcut way of expanding a binomial.

 
 
notebook Example 2:  Evaluate the binomial coefficient 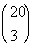example 2a.

 
Looks like we are going to need to use the definition of a binomial coefficient to help us out on this.
 

Looking at the definition of binomial coefficient, what is n?

If you said 20, you are correct!!!  n is the top number, which in this case is 20.
 

Looking at the definition of binomial coefficient, what is r?

If you said 3, give yourself a pat on the back!!!!   r is the bottom number, which in this case is 3.
 

Putting those values into the definition of a binomial coefficient we get:
 

example 2b

 
 

*n = 20, r = 3
 
 

*Eval. inside ( )

*Expand 20! until it gets to 17!
  which is the larger ! in the den.

*Cancel out 17!'s
 

 
 

If you have a factorial key, you can put it in as 20! divided by 17! divided by 3! and then press enter or =.

If you don't have a factorial key, you can simplify it as shown above and then enter it in.  It is probably best to simplify it first, because in some cases the numbers can get rather large, and it would be cumbersome to multiply all those numbers one by one.

The final answer is 1140. 
 
 

notebook Example 3:  Evaluate the binomial coefficient 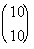example 3a.

 
Looks like we are going to need to use the definition of a binomial coefficient to help us out on this.
 

Looking at the definition of binomial coefficient, what is n?

If you said 10, you are correct!!!  n is the top number, which in this case is 10.
 

Looking at the definition of binomial coefficient, what is r?

If you said 10, give yourself a pat on the back!!!!   r is the bottom number, which in this case is 10.
 

Putting those values into the definition of a binomial coefficient we get:
 

example 3b

 
 

*n = 10, r = 10
 
 

*Eval. inside ( )
 

*0! = 1
*Cancel out 10!'s
 

 
 

If you have a factorial key, you can put it in as 10! divided by 0! divided by 10! and then press enter or =.

If you don't have a factorial key, you can simplify it as shown above and then enter it in.  It is probably best to simplify it first, because in some cases the numbers can get rather large, and it would be cumbersome to multiply all those numbers one by one.

The final answer is 1. 
 
 

notebook Example 4:  Evaluate the binomial coefficient 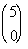example 4a.

 
Looks like we are going to need to use the definition of a binomial coefficient to help us out on this.
 

Looking at the definition of binomial coefficient, what is n?

If you said 5, you are correct!!!  n is the top number, which in this case is 5.
 

Looking at the definition of binomial coefficient, what is r?

If you said 0, give yourself a pat on the back!!!!   r is the bottom number, which in this case is 0.
 

Putting those values into the definition of a binomial coefficient we get:
 

example 4b

 
 

*n = 5, r = 0
 
 

*Eval. inside ( )
 

*0! = 1
*Cancel out 5!'s
 

 
 

If you have a factorial key, you can put it in as 5! divided by 5! divided by 0! and then press enter or =.

If you don't have a factorial key, you can simplify it as shown above and then enter it in.  It is probably best to simplify it first, because in some cases the numbers can get rather large, and it would be cumbersome to multiply all those numbers one by one.

The final answer is 1. 


  Binomial Theorem

For any positive integer n:

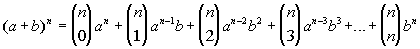
binomial theorem
 

Some things to note about this theorem:

The top number of the binomial coefficient is always n, which is the exponent on your binomial.

The bottom number of the binomial coefficient starts with 0 and goes up 1 each time until you reach n, which is the exponent on your binomial. 

The 1st term of the expansion has a (first term of the binomial) raised to the n power, which is the exponent on your binomial.  From there a's exponent goes down 1, until the last term, where it is being raised to the 0 power; which is why you don't see it written.

The first term of the expansion has b (second term of the binomial) raised to the 0 power, which is why you don't see it written.  From there b's exponent goes up 1, until the last term, where it is being raised to the nth power, which is the exponent on your binomial.
 
 
 

notebook Example 5:  Use the Binomial Theorem to expand the binomial 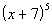example 5a.   Simplify the result.

 
Looks like we are going to need to use the Binomial Theorem to help us out on this.

Looking at the Binomial Theorem, what is a?

If you said x, you are correct!!! a is the first term of the binomial, which in this case is x.
 

Looking at the Binomial Theorem, what is b?

If you said 7, give yourself a pat on the back!!!!   b is the second term of the binomial, which in this case is 7.
 

Looking at the Binomial Theorem, what is n?

If you said 5, give yourself a high five!!!!   n is the exponent on the binomial, which in this case is 5.
 

Putting those values into the Binomial Theorem we get:
 

example 5b

 
 
 
 

*a = x, b = 7, n = 5
 
 
 
 
 
 

*Use definition of
binomial coefficient

*Eval. 7's raised to exponents
 
 
 
 

*Eval. inside ( )
 
 
 
 
 

*Expand num. until it gets to
larger ! in the den.
 
 

*Cancel out !'s
 
 
 
 
 

*Simplify
 
 

 
 

If you have a factorial key, you can put in the binomial coefficient part of each term as the (top number)! divided by the (first number in the denominator) ! divided by the (second number in the denominator)! and then press enter or =.

If you don't have a factorial key, you can simplify it as shown above and then enter it in.  It is probably best to simplify it first, because in some cases the numbers can get rather large, and it would be cumbersome to multiply all those numbers one by one.

So our final answer is 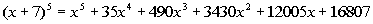example 5c.
 
 

notebook Example 6:  Use the Binomial Theorem to expand the binomial 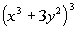example 6a.   Simplify the result.

 
Looks like we are going to need to use the Binomial Theorem to help us out on this.

Looking at the Binomial Theorem, what is a?

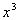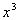If you said example 6b, you are correct!!!  a is the first term of the binomial, which in this case is example 6b.
 

Looking at the Binomial Theorem, what is b?

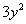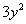If you said example 6c, give yourself a pat on the back!!!!   b is the second term of the binomial, which in this case is example 6c.
 

Looking at the Binomial Theorem, what is n?

If you said 3, give yourself a high five!!!!   n is the exponent on the binomial, which in this case is 3.
 

Putting those values into the Binomial Theorem we get:
 

example 6d

 
 
 
 

*a = x^3, b = 3y^2, n = 3
 
 
 
 
 
 

*Use definition of binomial coefficient

*Eval. x^3's and 3y^2's raised to exponents
 
 
 
 

*Eval. inside ( )
 
 
 
 
 

*Expand num. until it gets to larger ! in the den.
 
 

*Cancel out !'s
 
 

*Simplify
 

 
 

If you have a factorial key, you can put in the binomial coefficient part of each term as the (top number)! divided by the (first number in the denominator) ! divided by the (second number in the denominator)! and then press enter or =.

If you don't have a factorial key, you can simplify it as shown above and then enter it in.  It is probably best to simplify it first, because in some cases the numbers can get rather large, and it would be cumbersome to multiply all those numbers one by one.

So our final answer is 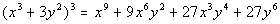example 6e.
 
 

notebook Example 7:  Use the Binomial Theorem to expand the binomial 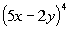example 7a.   Simplify the result.

 
Looks like we are going to need to use the Binomial Theorem to help us out on this.

Looking at the Binomial Theorem, what is a?

If you said 5x, you are correct!!! a is the first term of the binomial, which in this case is 5x.
 

Looking at the Binomial Theorem, what is b?

If you said -2y, give yourself a pat on the back!!!!   b is the second term of the binomial, which in this case is -2y.

Be careful here.  The way the Binomial Theorem is written, whatever sign is in front of b is part of b's value.  Since there was a - in front of 2y, b's value includes the -.
 

Looking at the Binomial Theorem, what is n?

If you said 4, give yourself a high five!!!!   n is the exponent on the binomial, which in this case is 4.
 

Putting those values into the Binomial Theorem we get:
 

example 7b

 
 
 
 

*a = 5x, b = -2y,
n = 4
 
 

*Use definition of
binomial coefficient

*Eval.  5x's and -2y's raised to exponents
 
 
 

*Eval. inside ( )
 
 
 
 

*Expand num. until it gets to
larger ! in the den.
 
 
 

*Cancel out !'s
 
 
 
 

*Simplify
 

 
 

If you have a factorial key, you can put in the binomial coefficient part of each term as the (top number)! divided by the (first number in the denominator) ! divided by the (second number in the denominator)! and then press enter or =.

If you don't have a factorial key, you can simplify it as shown above and then enter it in.  It is probably best to simplify it first, because in some cases the numbers can get rather large, and it would be cumbersome to multiply all those numbers one by one.

So our final answer is 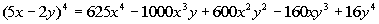example 7c.
 


  Finding a Particular Term in a Binomial Expansion

The rth term of the expansion of 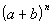term 1 is

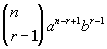
term 2
 
 

Some things to note about the rth term:

The top number of the binomial coefficient is n, which is the exponent on your binomial.

The bottom number of the binomial coefficient is r - 1, where r is the term number.

a is the first term of the binomial and its exponent is n - r + 1, where n is the exponent on the binomial and r is the term number.

b is the second term of the binomial and its exponent is r - 1, where r is the term number.
 
 

notebook Example 8:  Find the fourth term of the expansion 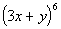example 8a.   Simplify the result.

 
Looks like we are going to need to use the rth term expansion formula to help us out on this.
 

Looking at the rth term expansion formula, what is n?

If you said 6, you are correct!!!  n is the exponent on your binomial, which in this case is 6.
 

Looking at the rth term expansion formula, what is r?

If you said 4, give your self a pat on the back!!!!   r is the number of the term to be found, which in this case is 4.
 

Looking at the rth term expansion formula, what is a?

If you said 3x, you are correct!!!  a is the first term of the binomial, which in this case is 3x.
 

Looking at the rth term expansion formula, what is b?

If you said y, give yourself a pat on the back!!!!   b is the second term of the binomial, which in this case is y. 
 

Putting those values into the rth term expansion formula we get:
 

example 8b
*n = 6, r = 4, a = 3x, b = y
 
 
 
 
 

*Use definition of binomial coefficient
 
 
 

*Eval. inside ( )
 

*Expand 6! until it gets to 3!
which is the larger ! in the den.
 
 

*Cancel out !'s
 

*Simplify
 
 

If you have a factorial key, you can put the binomial coefficient in as 6! divided by 3! divided by 3! and then press enter or =.

If you don't have a factorial key, you can simplify it as shown above and then enter it in.  It is probably best to simplify it first, because in some cases the numbers can get rather large, and it would be cumbersome to multiply all those numbers one by one.

This would tell us that the 4th term of the binomial 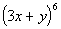example 8a  would be 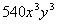example 8c. 
 
 

notebook Example 9:  Find the fifth term of the expansion 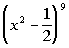example 9a.   Simplify the result.

 
Looks like we are going to need to use the rth term expansion formula to help us out on this.
 

Looking at the rth term expansion formula, what is n?

If you said 9, you are correct!!!  n is the exponent on your binomial, which in this case is 9.
 

Looking at the rth term expansion formula, what is r?

If you said 5, give your self a pat on the back!!!!   r is the number of the term to be found, which in this case is 5.
 

Looking at the rth term expansion formula, what is a?

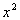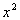If you said example 9d, you are correct!!!  a is the first term of the binomial, which in this case is example 9d.
 

Looking at the rth term expansion formula, what is b?

If you said -1/2, give yourself a pat on the back!!!!   b is the second term of the binomial, which in this case is -1/2. 

Be careful here.  The way the formula for the rth term of a binomial expansion is written, whatever sign is in front of b is part of b's value.  Since there was a - in front of 1/2, b's value includes the -.
 

Putting those values into the rth term expansion formula we get:
 

example 9b
*n = 9, r = 5, a = x^2, b = -1/2
 
 
 
 
 

*Use definition of binomial coefficient
 

*Eval. inside ( )
 

*Expand 9! until it gets to 5!
which is the larger ! in the den.

*Cancel out !'s
 
 
 
 
 

*Simplify
 
 

If you have a factorial key, you can put the binomial coefficient in as 9! divided by 5! divided by 4! and then press enter or =.

If you don't have a factorial key, you can simplify it as shown above and then enter it in.  It is probably best to simplify it first, because in some cases the numbers can get rather large, and it would be cumbersome to multiply all those numbers one by one.

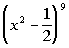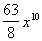This would tell us that the 5th term of the binomial example 9a would be example 9c. 
 

 

desk Practice Problems


These are practice problems to help bring you to the next level.  It will allow you to check and see if you have an understanding of these types of problems. Math works just like anything else, if you want to get good at it, then you need to practice it.  Even the best athletes and musicians had help along the way and lots of practice, practice, practice, to get good at their sport or instrument.  In fact there is no such thing as too much practice.

To get the most out of these, you should work the problem out on your own and then check your answer by clicking on the link for the answer/discussion for that  problem.  At the link you will find the answer as well as any steps that went into finding that answer.

pencil Practice Problems 1a - 1b: Evaluate the binomial coefficient.


1a. problem 1a
(answer/discussion to 1a)
1b. problem 1b
(answer/discussion to 1b)



pencil Practice Problems 2a - 2b: Use the Binomial Theorem to expand the binomial.   Simplify the results.


2a. problem 2a
(answer/discussion to 2a)
2b. problem 2b
(answer/discussion to 2b)



pencil Practice Problems 3a - 3b: Find the given term of the expansion.  Simplify the results.


3a. problem 3a;  fifth term
(answer/discussion to 3a)
3b. prolbme 3b  ;   fourth term
(answer/discussion to 3b)


 

 

desk Need Extra Help on these Topics?


There were no good websites found to help us with the topics on this page.

 

Go to Get Help Outside the Classroom found in Tutorial 1: How to Succeed in a Math Class for some more suggestions.


 

buffalo top  

WTAMU > Virtual Math Lab > College Algebra


Last revised on May 19, 2011 by Kim Seward.
All contents copyright (C) 2002 - 2011, WTAMU and Kim Seward. All rights reserved.