College Algebra Tutorial 50


College Algebra
Answer/Discussion to Practice Problems  
Tutorial 50: Solving Systems of
Linear Equations in Three Variables

WTAMU > Virtual Math Lab > College Algebra > Tutorial 50: Solving Systems of Linear Equations in Three Variables


 

checkAnswer/Discussion to 1a

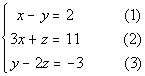
problem 1a
 

Note that the numbers in (  ) are equation numbers.  They will be used throughout the problems for reference purposes.

Basically, we are going to do the same thing we did with the systems of two equations, just more of it.  In other words, we will have to do the elimination twice, to get down to just one variable since we are starting with three variables this time.
 

Step 1: Simplify and put all three equations in the form Ax + By + Cz = D if needed .

 
No simplification needed here.  Let's go on to the next step.

 
 
Step 2: Choose to eliminate any one of the variables from any pair of equations.

 
Let's start by picking our first variable to eliminate.  I'm going to pick z to eliminate.  I need to do this with ANY pair of equations.
 

Note how equation (1) already has z eliminated.  We can use this as our first equation with z eliminated
 

Using equation (1) as one of our equations where z is eliminated:
 

ad1a
*equation (1)

 
Now we can't just stop here for of two reasons.  First, we would be stuck because we have one equation and two unknowns.  Second, when we solve a system it has to be a solution of ALL equations involved and we have not incorporated the third equation yet.  Let's do that now. 

 
 
Step 3:  Eliminate the SAME variable chosen in step 2 from any other pair of equations creating a system of two equations and 2 unknowns.

 
We are still going after eliminating z, this time we want to use the second and the third equations.  

It looks like we will have to multiply the second equation by 2, to get opposites on z. 

Multiplying the second equation by 2 and then adding that to equation (3) we get:
 

ad1a2
*Mult. eq. (2) by 2
 
 

*z's have opposite coefficients
*z's dropped out
 
 
 

Step 4:  Solve the remaining system found in step 2 and 3, just as discussed in Tutorial 49: Solving a System of Linear Equations in Two variables.

 
Putting the two equations that we have found together, we now have a system of two equations and two unknowns, which we can solve just like the ones shown in Tutorial 49: Solving a System of Linear Equations in Two variables.  You can use either elimination or substitution.  I'm going to go ahead and stick with the elimination method to complete this. 

Let's first put those equations together:
 

ad1a3
*Put equations found in steps 2 and 3
together into one system

 
Now I'm going to choose y to eliminate.  It looks like they already have opposite coefficients, so we just need to add the two equations together.
 

I'm going to go ahead and add the equations together:
 

ad1a4

*y's have opposite coefficients
*y's dropped out
 

 
Solving for x we get:

 
ad1a5
*Solve for x
 

*x is 3
 
 

If we go back one step to the system that had two equations and two variables and put in 3 for x in what is labeled equation 1, we would get:

 
ad1a6
*Eq. (1)
*Plug in 3 for x
*Solve for y
 

*y is 1 
 
 

Step 5:  Solve for the third variable.

 
Now we need to go back to the original system and pick any equation to plug in the two known variables and solve for our last variable.

I choose equation (2) to plug in our 3 for x that we found:
 

ad1a7
*Eq. (2)
*Plug in 3 for x

*Solve for z

*z is 2
 
 

Step 6:  Check.

 
You will find that if you plug the ordered triple (3, 1, 2) into ALL THREE equations of the original system, this is a solution to ALL THREE of them.

(3, 1, 2) is a solution to our system.
 

(return to problem 1a)


 

checkAnswer/Discussion to 1b

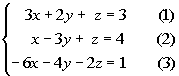
problem 1b
 

Note that the numbers in (  ) are equation numbers.  They will be used throughout the problems for reference purposes.

Basically, we are going to do the same thing we did with the systems of two equations, just more of it.  In other words, we will have to do the elimination twice, to get down to just one variable since we are starting with three variables this time.
 

Step 1: Simplify and put all three equations in the form Ax + By + Cz = D if needed .

 
No simplification needed here.  Let's go on to the next step.

 
 
Step 2: Choose to eliminate any one of the variables from any pair of equations.

 
Let's start by picking our first variable to eliminate.  I'm going to choose z to eliminate.  I need to do this with ANY pair of equations.

Let's first eliminate z using the first and second equations.  

If I multiply -1 times the second equation, then the z terms will be opposites of each other and ultimately drop out.

Multiplying -1 times the second equation and then adding that to the first equation we get:
 

ad1b1

*Mult. eq. (2) by -1
 
 

*z's have opposite coefficients
*z's dropped out

 
 

Now we can't just stop here for of two reasons.  First, we would be stuck because we have one equation and two unknowns.  Second, when we solve a system it has to be a solution of ALL equations involved and we have not incorporated the third equation yet.  Let's do that now. 

 
 
Step 3:  Eliminate the SAME variable chosen in step 2 from any other pair of equations creating a system of two equations and 2 unknowns.

 
We are still going after eliminating z, this time we want to use the first and the third equations.  

It looks like we will have to multiply the first equation by 2, to get opposites on z. 

Multiplying the first equation by 2 and then adding that to equation (3) we get:
 

ad1b2
*Mult. eq. (1) by 2
 
 

*z's have opposite coefficients
*z's dropped out
 
 

Wait a minute, where did our variables go???? 

As mentioned above, if the variable drops out AND we have a FALSE statement, then we have no solutions. 
 
 

Step 4:  Solve the remaining system found in step 2 and 3, just as discussed in Tutorial 49: Solving a System of Linear Equations in Two variables.

 
Since we did not get a value for our variables, there is nothing to solve here.

 
 
Step 5:  Solve for the third variable.

 
Since we did not get a value for our variables, there is nothing to plug in here.

 
 
Step 6:  Check.

 
There is no value to plug in here. 

The answer is no solution.
 

(return to problem 1b)


 

checkAnswer/Discussion to 1c

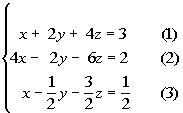
problem 1c
 

Note that the numbers in (  ) are equation numbers.  They will be used throughout the problems for reference purposes.

Basically, we are going to do the same thing we did with the systems of two equations, just more of it.  In other words, we will have to do the elimination twice, to get down to just one variable since we are starting with three variables this time.
 

Step 1: Simplify and put all three equations in the form Ax + By + Cz = D if needed .

 
It looks like we have some fractions to get rid of.

Multiplying equation (3) by its LCD we get:
 

ad1c1

 
 

*Multiply eq. (3) by LCD of 2
 
 
 
 
 
 
 
 
 

Step 2: Choose to eliminate any one of the variables from any pair of equations.

 
Let's start by picking our first variable to eliminate.  I'm going to choose y to eliminate.  I need to do this with ANY pair of equations.

Let's first eliminate y using the first and second equations.  

It looks like the y's already have opposite coefficients so all we need to do is add the two equations and the y's will drop out.

Adding equations (1) and (2) together we get:
 

ad1c2

*y's have opposite coefficients
*y's dropped out

 
 

Now we can't just stop here for of two reasons.  First, we would be stuck because we have one equation and two unknowns.  Second, when we solve a system it has to be a solution of ALL equations involved and we have not incorporated the third equation yet.  Let's do that now. 

 
 
Step 3:  Eliminate the SAME variable chosen in step 2 from any other pair of equations creating a system of two equations and 2 unknowns.

 
We are still going after eliminating y, this time we want to use the first and the third equations.  

It looks like we will have to multiply the third equation by 2, to get opposites on y. 

Multiplying the third equation by 2 and then adding that to equation (1) we get:
 

ad1c3
*Mult. eq. (3) by 2
 
 

*y's have opposite coefficients
*y's dropped out
 
 
 

Step 4:  Solve the remaining system found in step 2 and 3, just as discussed in Tutorial 49: Solving a System of Linear Equations in Two variables.

 
Putting the two equations that we have found together, we now have a system of two equations and two unknowns, which we can solve just like the ones shown in Tutorial 49: Solving a System of Linear Equations in Two variables.  You can use either elimination or substitution.  I'm going to go ahead and stick with the elimination method to complete this. 

Let's first put those equations together:
 

ad1c4
*Put equations found in steps 2 and 3
together into one system

 
Now I'm going to choose x to eliminate.  

It looks like we will have to multiply equation (5) by -1, to get opposites on x. 

Multiplying equation (5) by -1 and then adding that to equation (4) we get:
 

ad1c5

*Mult. eq. (5) by -1
 
 

*x's and z's have opposite coefficients
*x's and z's dropped out 
 
 

Wait a minute, where did our variables go???? 

As mentioned above, if the variable drops out AND we have a TRUE statement, then when have an infinite number of solutions. They end up being the same line.
 
 

Step 5:  Solve for the third variable.

 
Since we did not get a value for our variables, there is nothing to plug in here.

 
 
Step 6:  Check.

 
There is no value to plug in here. 

When they end up being the same equation, you have an infinite number of solutions. You can write up your answer by writing out any of the three equations to indicate that they are the same equation.

Three ways to write the answer are {(x, y, z)| x + 2y + 4z= 3} OR {(x, y, z)| 4x - 2y - 6z = 2} OR {(x, y, z)| x - 1/2y - 3/2z = 1/2}.
 

(return to problem 1c)

 

Buffalo top

 
WTAMU > Virtual Math Lab > College Algebra > Tutorial 50: Solving Systems of Linear Equations in Three Variables


Last revised on April 25, 2011 by Kim Seward.
All contents copyright (C) 2002 - 2011, WTAMU and Kim Seward. All rights reserved.