College Algebra
Tutorial 50: Solving Systems of
Linear Equations in Three Variables
 Learning Objectives Learning Objectives
After completing this tutorial, you should be able to:
- Solve a system of linear equations in three variables by the
elimination
method.
|
 Introduction Introduction
In this tutorial we will be specifically looking at
systems that have
three linear equations and three unknowns. In Tutorial
49: Solving Systems of Linear Equations in Two Variables we
covered
systems that have two linear equations and two unknowns. We will
only look at solving them using the elimination method. Don't get
overwhelmed by the length of some of these problems. Just keep in
mind that a lot of the steps are just like the ones from the
elimination
method of two equations and two unknowns that were covered in Tutorial
49: Solving Systems of Linear Equations in Two Variables, just more of
them. |
 Tutorial Tutorial
|
System of Linear Equations
|
A system of linear equations is two or more linear
equations that
are being solved simultaneously.
In this tutorial, we will be looking at systems that
have three linear
equations and three unknowns.
Tutorial 49:
Solving a System
of Linear Equations in Two Variables looked at three ways to
solve
linear equations in two variables. |
In general, a solution of a system in three
variables is an ordered
triple (x, y, z)
that makes ALL THREE equations true.
In other words, it is what they all three have in
common. So if
an ordered triple is a solution to one equation, but not another, then
it is NOT a solution to the system.
Note that the linear equations in two variables found in
Tutorial 49:
Solving a System of Linear Equations in Two Variables graphed to be a
line
on a two dimensional Cartesian coordinate system. If you were to
graph (which you won't be asked to do here) a linear equation in three
variables you would end up with a figure of a plane in a three
dimensional
coordinate system. An example of what a plane would look like is
a floor or a desk top.
Recall the following from
Tutorial 49: Solving
a System
of Linear Equations in Two Variables:
A consistent system is a system that has at
least one solution.
An inconsistent system is a system that has
no solution.
The equations of a system are dependent if ALL
the solutions
of one equation are also solutions of the other two equations. In
other words, they end up being the same line.
The equations of a system are independent if
they do not share
ALL solutions. They can have one point in common, just not
all
of them. |
There are three possible
outcomes that you
may encounter when working with these systems:
-
-
-
|
One Solution
If the system in three variables has one solution, it is
an ordered
triple (x, y, z)
that is a solution to ALL THREE equations. In other words,
when
you plug in the values of the ordered triple, it makes ALL THREE
equations
TRUE.
If you do get one solution for your final answer, is
this system consistent or inconsistent?
If you said consistent, give yourself a pat on the back!
If you do get one solution for your final answer, would
the equations be dependent or independent?
If you said independent, you are correct! |
No Solution
If the three planes are parallel to each other, they
will never
intersect. This means they do not have any points in
common.
In this situation, you would have no solution.
If you get no solution for your final answer, is
this system consistent or inconsistent?
If you said inconsistent, you are right!
If you get no solution for your final answer, would
the equations be dependent or independent?
If you said independent, you are correct! |
Infinite
Solutions
If the three planes end up lying on top of each other,
then there
is an infinite number of solutions. In this situation, they
would
end up being the same plane, so any solution that would work in one
equation
is going to work in the other.
If you get an infinite number of solutions for
your final answer, is
this system consistent or inconsistent?
If you said consistent you are right!
If you get an infinite number of solutions for
your final answer, would
the equations be dependent or independent?
If you said dependent you are correct! |
Solving Systems of Linear
Equations in Three Variables
Using the Elimination Method
|
Note that there is more than one way that you can solve
this type of
system. Elimination (or addition) method is one of the more
common
ways of doing it. So I choose to show it this way. If you have another way of doing it, by all means, do it
your way, then
you can check your final answers with mine. No matter which way
you
choose to do it, if you are doing it correctly, the answer is going
have
to be the same. |
Step 1: Simplify and
put all three equations in the form Ax + By + Cz = D if needed . |
This would involve things like removing ( ) and
removing fractions.
To remove ( ): just use the distributive property.
To remove fractions: since fractions are another way to
write division,
and the inverse of divide is to multiply, you remove fractions by
multiplying
both sides by the LCD of all of your fractions. |
Step 2: Choose to eliminate
any one of the variables from any pair of equations. |
|
At this point, you are only
working with two
of your equations. In the next step you will incorporate the
third
equation into the mix.
Looking ahead, you will be adding these two
equations together.
In that process you need to make sure that one of the variables drops
out,
leaving one equation and two unknowns. The only way you can
guarantee
that is if you are adding opposites. The sum of opposites
is 0.
It doesn't matter which variable you choose to drop
out.
You want to keep it as simple as possible. If a variable already
has opposite coefficients than go right to adding the two equations
together.
If they don't, you need to multiply one or both equations by a number
that
will create opposite coefficients in one of your variables. You
can
think of it like a LCD. Think about what number the original
coefficients
both go into and multiply each separate equation accordingly.
Make
sure that one variable is positive and the other is negative before you
add.
For example, if you had a 2x in one equation
and a 3x in another equation, you could
multiply
the first equation by 3 and get 6x and
the
second equation by -2 to get a -6x.
So
when you go to add these two together they will drop out. |
Step 3:
Eliminate
the SAME variable chosen in step 2 from any other pair of equations,
creating
a system of two equations and 2 unknowns. |
|
When you solve this system that has two equations and
two variables,
you will have the values for two of your variables.
Remember that if both variables drop out and
you have a FALSE
statement, that means your answer is no solution.
If both variables drop out and you have a TRUE
statement, that means
your answer is infinite solutions, which would be the equation of the
line. |
Step 5:
Solve for
the third variable. |
If you come up with a value for the two variables in
step 4, that
means the three equations have one solution. Plug the values
found in step 4 into any of the equations in the problem that have the
missing variable in it and solve for the third variable. |
You can plug in the proposed solution into ALL THREE
equations.
If it makes ALL THREE equations true then you have your solution to the
system.
If it makes at least one of them false, you need to go
back and redo
the problem. |
 Example
1 Example
1: Solve the system:
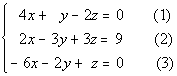 |
Note that the numbers in
( ) are equation
numbers. They will be used throughout the problems for reference
purposes.
Basically, we are going to do the same thing we did
with the systems
of two equations, just more of it. In other words, we will have
to
do the elimination twice, to get down to just one variable since we are
starting with three variables this time. |
| No simplification needed here. Let's go on to the
next step. |
Let’s start by picking our first variable to
eliminate. I’m going
to choose y to eliminate. I need
to do
this with ANY pair of equations.
Let’s first eliminate y using the first
and second equations. This process is identically to how we
approached
it with the systems found in Tutorial
49: Solving a System of Linear Equations in Two variables.
If I multiply 3 times the first equation, then the y terms will be opposites of each other and ultimately drop out.
Multiplying 3 times the first equation and then
adding that to the
second equation we get: |
|
*Mult. eq. (1) by 3
*y's
have opposite
coefficients
*y's
dropped out
|
Now we can’t just stop here for of two reasons.
First, we would
be stuck because we have one equation and two unknowns. Second,
when
we solve a system it has to be a solution of ALL equations involved and
we have not incorporated the third equation yet. Let’s do that
now. |
We are still going after eliminating y,
this time we want to use the first and the third equations. We
could
use the second and third, as long as we have not used both of the same
ones used in step 2 above.
It looks like we will have to multiply the first
equation by 2, to get
opposites on y.
Multiplying the first equation by 2 and then adding
that to equation
(3) we get: |
|
*Mult. eq. (1) by 2
*y's
have opposite
coefficients
*y's
dropped out
|
Putting the two equations that we have found together,
we now have
a system of two equations and two unknowns, which we can solve just
like
the ones shown in Tutorial 49: Solving a System of Linear Equations in
Two variables. You can use either elimination or
substitution.
I’m going to go ahead and stick with the elimination method to complete
this.
Let’s first put those equations together: |
|
*Put equations found in steps
2 and 3
together into one system |
Now I’m going to choose z to eliminate.
We can either multiply the first equation by -1 or the second, either
way
will create opposites in front of the z terms.
I’m going to go ahead and multiply equation (5) by -1
and then add
the equations together: |
|
*Mult. eq. (5) by -1
*z's
have opposite
coefficients
*z's
dropped out
|
If we go back one step to the system that had two
equations and
two variables and put in 3/4 for x in
what
is labeled equation 4, we would get: |
|
*Eq. (4)
*Plug in 3/4 for x
*Solve for z
*z is 1/2
|
Now we need to go back to the original system and pick
any equation
to plug in the two known variables and solve for our last variable.
I choose equation (1) to plug in our 2 for x and
1 for z that we found: |
|
*Eq. (1)
*Plug in 3/4 for x and 1/2 for z
*Solve for y
*y is -2 |
You will find that if you plug the ordered triple (3/4,
-2, 1/2) into
ALL THREE equations of the original system, this is a solution to ALL
THREE
of them.
(3/4, -2, 1/2) is a solution to our system. |
 Example
2 Example
2: Solve the system:
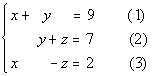 |
Note that the numbers in
( ) are equation
numbers. They will be used throughout the problems for reference
purposes.
Basically, we are going to do the same thing we did
with the systems
of two equations, just more of it. In other words, we will have
to
do the elimination twice, to get down to just one variable since we are
starting with three variables this time. |
No simplification needed here. Let's go on to the
next step. |
Let’s start by picking our first variable to
eliminate. I’m
going to pick z to eliminate.
I need
to do this with ANY pair of equations.
Note how equation (1) already has z eliminated.
We can use this as our first equation with z eliminated
Using equation (1) as one of our equations where z is eliminated: |
Now we can’t just stop here for of two reasons.
First, we would
be stuck because we have one equation and two unknowns. Second,
when
we solve a system it has to be a solution of ALL equations involved and
we have not incorporated the third equation yet. Let’s do that
now. |
We are still going after eliminating z,
this time we want to use the second and the third equations.
It looks like the z's
already have opposite
coefficients, so all we have to do is add these two equations
together.
Adding equations (2) and (3) together we get: |
|
*z's
have opposite
coefficients
*z's
dropped out
|
Putting the two equations that we have found together,
we now have
a system of two equations and two unknowns, which we can solve just
like
the ones shown in Tutorial 49: Solving a System of Linear Equations in
Two variables. You can use either elimination or
substitution.
I’m going to go ahead and stick with the elimination method to complete
this.
Let’s first put those equations together: |
|
*Put equations found in steps
2 and 3
together into one system |
Now I’m going to choose x to eliminate.
We can either multiply the first equation by -1 or the second, either
way
will create opposites in front of the z terms.
I’m going to go ahead and multiply equation (1) by -1
and then add
the equations together: |
|
*Mult. eq. (1) by -1
*x's
and y's
have opposite coefficients
*x's
and y's
dropped out
|
Wait a minute, where did our
variables go????
As mentioned above, if the variable drops out AND we
have a TRUE statement,
then when have an infinite number of solutions. They end up being the
same
line. |
Since we did not get a value for any of our variables,
there is nothing
to plug in here. |
There is no value to plug in here.
When they end up being the same equation, you have an
infinite number
of solutions. You can write up your answer by writing out any of the
three
equations to indicate that they are the same equation.
Three ways to write the answer are {(x, y, z)| x + y = 9} OR {(x, y, z)| y + z = 7} OR {(x, y, z)| x - z = 2}. |
 Example
3 Example
3: Solve the system:
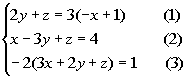 |
Note that the numbers in
( ) are equation
numbers. They will be used throughout the problems for reference
purposes.
Basically, we are going to do the same thing we did
with the systems
of two equations, just more of it. In other words, we will have
to
do the elimination twice, to get down to just one variable since we are
starting with three variables this time. |
It looks like we have to get rid of a few parenthesis
and line everything
up. |
|
*Use distributive property to
clear (
)
*Rewrite (1) and (3) in the
form Ax + By + Cz =
D
|
Let’s start by picking our first variable to
eliminate. I’m going
to choose z to eliminate. I need
to do
this with ANY pair of equations.
Let’s first eliminate z using the first
and second equations. This process is identically to how we
approached
it with the systems found in Tutorial
49: Solving a System of Linear Equations in Two variables.
If I multiply -1 times the second equation, then the z terms will be opposites of each other and ultimately drop out.
Multiplying -1 times the second equation and then
adding that to
the first equation we get: |
|
*Mult. eq. (2) by -1
*z's
have opposite
coefficients
*z's
dropped out
|
Now we can’t just stop here for of two reasons.
First, we would
be stuck because we have one equation and two unknowns. Second,
when
we solve a system it has to be a solution of ALL equations involved and
we have not incorporated the third equation yet. Let’s do that
now. |
We are still going after eliminating z,
this time we want to use the first and the third equations. We
could
use the second and third, as long as we have not used both of the same
ones used in step 2 above.
It looks like we will have to multiply the first
equation by 2, to get
opposites on z.
Multiplying the first equation by 2 and then adding
that to equation
(3) we get: |
|
*Mult. eq. (1) by 2
*x's, y's,
and z's have opposite coefficients
*x's, y's,
and z's dropped out
|
Wait a minute, where did our
variables go????
As mentioned above, if the variable drops out AND we
have a FALSE statement,
then we have no solutions. |
Since we did not get a value for our variables, there
is nothing to
solve here. |
Since we did not get a value for our variables, there
is nothing to
plug in here. |
There is no value to plug in here.
The answer is no solution. |
 Practice Problems Practice Problems
These are practice problems to help bring you to the next level.
It will allow you to check and see if you have an understanding of these
types of problems. Math works just like anything
else, if you want to get good at it, then you need to practice it.
Even the best athletes and musicians had help along the way and lots of
practice, practice, practice, to get good at their sport or instrument.
In fact there is no such thing as too much practice.
To get the most out of these, you should work the problem out on
your own and then check your answer by clicking on the link for the answer/discussion
for that problem. At the link you will find the answer
as well as any steps that went into finding that answer. |
 Practice Problems 1a - 1c: Solve each system. Practice Problems 1a - 1c: Solve each system.
 Need Extra Help on these Topics? Need Extra Help on these Topics?

Last revised on April 25, 2011 by Kim Seward.
All contents copyright (C) 2002 - 2011, WTAMU and Kim Seward. All rights reserved.
|
|


