College Algebra
Answer/Discussion to Practice Problems
Tutorial 32B: Inverse Functions

WTAMU > Virtual Math Lab > College Algebra > Tutorial 32B: Inverse Functions

Answer/Discussion to 1a

and

Let’s look at f(g(x)) first:

*Insert the "value" of g inside the function of f
*Plug in the "value" of g wherever there is an x the function f

Since BOTH f(g(x)) AND g(f(x)) would have to equal x for them to be inverses of each other and f(g(x)) is not equal to x, then we can stop here and say without a doubt that they are NOT inverses of each other.

(return to problem 1a)

Answer/Discussion to 1b

and

Let’s look at f(g(x)) first:

*Insert the "value" of g inside the function of f

*Plug in the "value" of g wherever there is an x the function f

Next, let’s look at g(f(x)):

*Insert the "value" of f inside the function of g

*Plug in the "value" of f wherever there is an x the function g

Since f(g(x)) AND g(f(x)) BOTH came out to be x, this proves that the two functions are inverses of each other.

(return to problem 1b)

Answer/Discussion to 2a

a) find the equation of

Step 1: Replace f(x) with y.

Step 2: Interchange x with y.

Step 3: Solve for y.

*Inverse of cube root is cubing both sides

*Inverse of -2 is + 2

Since this y is a function, it is the inverse of the original function.

Step 4: If f has an inverse function, replace y with .

b) graph f and

See how the graphs of f and

are mirrored images across the line y = x? Note how the ordered pairs are interchanged … for example (2, 0) is a point on f where (0, 2) is a point on

If you need a review on graphing the cubic functions, feel free to go to College Algebra Tutorial 31: Graphs of Functions, Part I.

c) indicate the domain and range of f and using interval notation

The domain of f is the same as the range of which is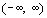

The range of f is the same as the domain of which is .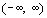

If you need a review on finding the domain and range of a function, feel free to go to College Algebra Tutorial 30: Introduction to Functions.

If you need a review on finding the domain and range of a graph of a function, feel free to go to College Algebra Tutorial 32: Graphs of Functions, Part II.

(return to problem 2a)

Answer/Discussion to 2b

a) find the equation of

Step 1: Replace f(x) with y.

Step 2: Interchange x with y.

Step 3: Solve for y.

*Inverse of - 2 is + 2

*Inverse of squaring is to take the square root

Normally when we take the square root of both sides, there are two answers .. the + or – of the square root. But, because it is only defined for greater than or equal to 0, then that means we can only use the positive square root.

If we had both + and – in front of the square root, then this would not be a function and hence there would not be an inverse. But, we do have a function here, so we can carry on ….

Since this y is a function, it is the inverse of the original function.

Step 4: If f has an inverse function, replace y with .

b) graph f and

See how the graphs of f and

are mirrored images across the line y = x? Note how the ordered pairs are interchanged … for example (0, -2) is a point on f where (-2, 0) is a point on

.

If you need a review on graphing the quadratic and square root functions, feel free to go to College Algebra Tutorial 31: Graphs of Functions, Part I.

c) indicate the domain and range of f and using interval notation

The domain of f is the same as the range of which is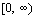

The range of f is the same as the domain of which is .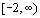

If you need a review on finding the domain and range of a function, feel free to go to College Algebra Tutorial 30: Introduction to Functions.

If you need a review on finding the domain and range of a graph of a function, feel free to go to College Algebra Tutorial 32: Graphs of Functions, Part II.

(return to problem 2b)

WTAMU > Virtual Math Lab > College Algebra >Tutorial 32B: Inverse Functions