College Algebra
Tutorial 32B: Inverse Functions
 Learning Objectives
After completing this tutorial, you should be able to:
- Verify inverse function.
- Find the inverse of a function.
- Graph a function and its inverse on the same
rectangular
coordinate system.
- Determine that a function has an inverse by using the
horizontal line test.
|
Introduction
In this tutorial we are going to learn
about inverse
functions. Inverse functions are
functions in their own right …they take on all of the same attributes.
If you
need a review on functions, feel free to go to College Algebra Tutorial
30: Introduction to Functions. What is special about the
inverse function is its relationship to
the function to which it is an inverse. We
will learn how to determine if a function has an
inverse and if so
how to find it. Basically what happens
is that x and y get interchanged and you solve
for y, which forces you to
apply
inverse operations. Consequently, you
will find that the domain of a function is the range of its inverse and
vice
versa. Invert away … |
Tutorial
|
Definition
of Inverse of a Function
|
Let f and g be two functions such
that
f(g(x))
= x,
for
every x in the domain of g
g(f(x))
= x,
for
every x in the domain of f,
then the function g is said to be the inverse of the
function f and is denoted  .
The domain of f is
equal to the range of and
the range
of f is
the domain of .
|
Let’s look at f(g(x))
first:
|
|
*Insert the
"value" of g inside the function
of f
*Plug in the
"value" of g wherever there is an x the function f
|
Next, let’s look at g(f(x)): |
|
*Insert the
"value" of f inside the function
of g
*Plug in the
"value" of f wherever there is an x the function g |
Since f(g(x))
AND g(f(x)) BOTH came out to be x, this
proves that the two functions are inverses of each other. |
Let’s look at f(g(x))
first:
|
|
*Insert the
"value" of g inside the function of f
*Plug in the
"value" of g wherever there is an x the function f |
Since BOTH f(g(x))
AND g(f(x)) would have to equal x for them
to be inverses of each other and f(g(x)) is not
equal to x, then we can stop
here and say without a doubt that they are NOT inverses of each
other.
|
|
The Horizontal Line Test for Inverse Functions
|
If NO horizontal line can be drawn so
that it intersects a
graph of a function f more than once, then the function f has an inverse
function
The next two examples illustrate this concept.
|
 Example 3: Use the
horizontal line test to determine if the
graph of the function has an inverse.
|
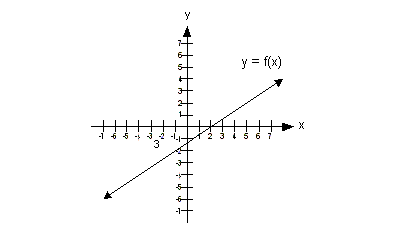
This graph would pass the horizontal
line test, because there
would not be any place on it that we could draw a horizontal line where
it would
intersect the graph of the function in more than one place.
Therefore, this function has an
inverse function.
|
Example 4: Use the
horizontal line test to determine if the
graph of the function has an inverse.
|
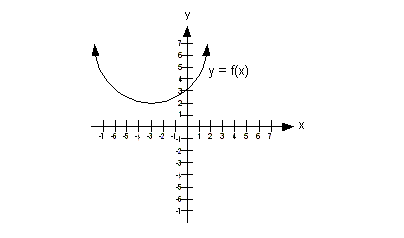
This function would not pass the
horizontal line test
because there is at least one place on it that we could draw a
horizontal line
and intersect it in more than one place. In fact, there are a lot
of
horizontal lines that we can draw that would intersect it in more than
one
place, but we only need to show one to say this function does not have
an
inverse function.
The graph below shows one horizontal
line drawn through our
graph that intersects it in two places:
Therefore this function does not
have an inverse.
|
|
Finding the Inverse of a Function
|
Step 1: Replace f(x)
with y.
|
Step 2: Interchange x with y.
|
If this y is a function, it is
the inverse of the original
function.
If this y is NOT a function, there is no inverse. |
Step 4: If f has an inverse
function, then replace y with . |
Example 5: Find the equation of the
inverse function for the function
 .
|
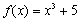Step 1: Replace f(x)
with y.
|
Step 2: Interchange x with y.
|
|
*Inverse of - 5 is + 5
*Inverse operation is
take the cube root of both side |
Since this y is a function, it
is the inverse of the original
function.
|
Step 4: If f has an inverse
function, replace y with . |
Example 6: Find the equation of the
inverse function for the function  .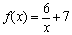
|
Step 1: Replace f(x)
with y.
|
Step 2: Interchange x with y.
|
|
*Mult. both sides by the LCD
of y
*Inverse of -7y is + 7y
*Factor out a y
*Inverse of mult. by x - 7 is divide by x - 7
|
Since this y is a function, it
is the inverse of the original
function.
|
Step 4: If f has an inverse
function, replace y with . |
Graphing a Function and it's
Inverse on the Same Coordinate System
|
The graph of is a
reflection of the
graph of the function f about the line y = x.
The next two examples will illustrate
this.
|
Example 7: a) find the equation of , b) graph f and and c)
indicate the domain and range of f and using interval
notation .
|
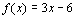
a)
find the equation of |
Step 1: Replace f(x)
with y.
|
Step 2: Interchange x with y.
|
|
*Inverse of -6 is + 6
*Inverse of mult. by 3y
is divide by 3y
|
Since this y is a function, it
is the inverse of the original
function.
|
Step 4: If f has an inverse
function, replace y with . |
c)
indicate the domain and range of f and using interval
notation |
The
domain of f is the same as the range of which is  .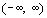
The range of f is the same as
the domain of which is .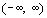
If you need a review on
finding the domain and range of a function, feel free to go to College
Algebra Tutorial
30: Introduction to Functions.
If you need a review on finding the
domain and range of a graph of a function, feel
free to go to College Algebra Tutorial
32: Graphs of Functions, Part II. |
Example 8: a) find the equation of , b) graph f and and c)
indicate the domain and range of f and using interval
notation .
|
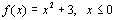
a) find the equation of |
Step 1: Replace f(x)
with y.
|
Step 2: Interchange x with y.
|
|
*Inverse of +3 is -3
*Inverse of squaring is
to take the square root
|
| Normally
when we take the square root of both sides, there
are two answers .. the + or – of the square root. But,
because it is only defined for y less than or equal to 0,
then that means we can only use the negative square root.
If we had both + and – in front of the
square root, then
this would not be a function and hence there would not be an inverse.
But, we
do have a function here, so we can carry on …. Since this y is a function, it
is the inverse of the original
function.
|
Step 4: If f has an inverse
function, replace y with . |
b) graph f and
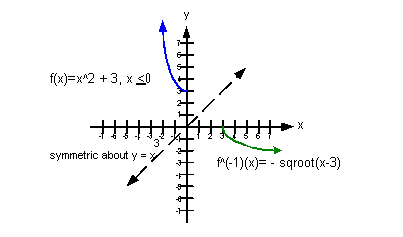
See how the
graphs of f and are
mirrored images across the line y = x? Note how the ordered pairs are interchanged … for
example (0, 3) is a
point on f where (3, 0) is a point on .
If you need a review on graphing the quadratic and square root
functions, feel free to go to College Algebra Tutorial
31: Graphs of Functions, Part I.
|
c)
indicate the domain and range of f and using interval
notation |
The
domain of f is the same as the range of which is  .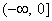
The range of f is the same as
the domain of which is  .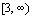
If you need a review on
finding the domain and range of a function, feel free to go to College
Algebra Tutorial
30: Introduction to Functions.
If you need a review on finding the
domain and range of a graph of a function, feel
free to go to College Algebra Tutorial
32: Graphs of Functions, Part II. |
Practice Problems
These are practice problems to help bring you to the next level.
It will allow you to check and see if you have an understanding of these
types of problems. Math works just like anything
else, if you want to get good at it, then you need to practice it.
Even the best athletes and musicians had help along the way and lots of
practice, practice, practice, to get good at their sport or instrument.
In fact there is no such thing as too much practice. To get the most out of these, you should work the problem out on
your own and then check your answer by clicking on the link for the answer/discussion
for that problem. At the link you will find the answer
as well as any steps that went into finding that answer. |
 Practice
Problems 1a - 1b: Use the
definition of inverse functions to
determine if the functions f and g are inverses of each
other.
Practice
Problems 2a - 2b: Given the function: a) find
the equation of , b) graph f and and c) indicate the domain and range of f and using
interval notation.
Need Extra Help on these Topics?
Last revised on June 24, 2010 by Kim Seward.
All contents copyright (C) 2002 - 2010, WTAMU and Kim Seward. All rights reserved.
|
|
and 
.
and 
.
and 
and 
