College Algebra
Answer/Discussion to Practice Problems
Tutorial 28: Parallel and Perpendicular Lines
 Answer/Discussion
to 1a
|
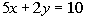
Before we tackle finding the parallel and perpendicular slopes it really
can help us out if we find the slope of the given line.
Recall that when you are given the equation of a line that you can find
the slope of it by writing it in the slope/intercept
form,  ,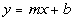
where m is the slope and b is
the y-intercept of the line.
Rewriting this equation in the slope/intercept form we get: |
|
*Inverse of add. 5x is sub. 5x
*Inverse of mult. by 2 is div. by 2
*Written in slope/intercept form
|
Lining up the form with the equation we got, can you see what the
slope is?
If you said -5/2, you are correct!!!
Slope of the parallel line:
Since parallel lines have the same slope what do you think the slope
of the parallel line is going to be? Pat yourself on the back if you said
-5/2.
Slope of the perpendicular line:
Since the slopes of perpendicular lines are negative reciprocals of
each other, what do you think the slope of the perpendicular line is?
Give yourself a high five if you said 2/5.
Remember that you take the reciprocal which is -2/5 and then you negate
it to get the 2/5 for your perpendicular slope.
The slope of the parallel line is -5/2 and the slope of the perpendicular
line is 2/5. |
Answer/Discussion
to 1b
|
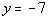
Do you remember what special type of line this equation is? It
is a horizontal line. If you need a review on horizontal lines, feel
free to go to Tutorial
27: Graphing Lines.
What is the slope of a horizontal line? If you said 0,
you are right on.
Slope of the parallel line:
Since parallel lines have the same slope, what do you think the slope
of the parallel line is going to be? Pat yourself on the back if you said
0.
Slope of the perpendicular line:
Since slopes of perpendicular lines are negative reciprocals of each
other, what do you think the slope of the perpendicular line is?
This one is a little trickier. Vertical lines and horizontal lines
are perpendicular to each other. The slope of the perpendicular line
in this case would be the slope of a vertical line which would be undefined.
The slope of the parallel line is 0 and the slope of the perpendicular
line is undefined. |
Answer/Discussion
to 1c
|
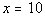
Do you remember what special type of line this equation is? It
is a vertical line. If you need a review on vertical lines, feel
free to go to Tutorial
27: Graphing Lines.
What is the slope of a vertical line? If you said undefined,
you are right on.
Slope of the parallel line:
Since parallel lines have the same slope, what do you think the slope
of the parallel line is going to be? Pat yourself on the back if you said
undefined.
Slope of the perpendicular line:
Since slopes of perpendicular lines are negative reciprocals of each
other, what do you think the slope of the perpendicular line is?
This one is a little trickier. Vertical lines and horizontal lines
are perpendicular to each other. The slope of the perpendicular line
in this case would be the slope of a horizontal line which would be 0.
The slope of the parallel line is undefined and the slope of the
perpendicular line is 0. |
Answer/Discussion
to 2a
Passes through (-7, 2) and is parallel to  . |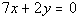
What are the two things we need to write an equation of a line????
If you said any point on the line and the slope, you are correct.
We have a point, however what about the slope? Does this mean
we can't work out the problem? You are not going to get off that
easily.
We need to do a little digging to get our slope.
As mentioned above, parallel
lines have the same slope. So, if we know the slope of the
line parallel to our line, we have it made.
Let's find the slope of the given line: |
|
*Inverse of add. 7x is sub. 7x
*Inverse of mult. by 2 is div. by 2
*Slope/intercept form of the line
|
Now keep in mind that this is not the equation of our line but of the
line parallel to our line. We needed to write it this way so we could
get the slope. And it looks like the slope is -7/2. Since our
line is parallel to a line that has a slope of -7/2, our line also has
a slope of -7/2.
OK, now we have our slope, which is -7/2. Now it is just like
problems in Tutorial 26: Equations
of Lines, we put the slope and one point into the point/slope equation.
Point/Slope Form: |
|
*Point/slope form of the line
|
Make sure that you are careful when one of your values is negative
and you have to subtract it as we did in line 2. x - (-7) is not the same as x - 7. |
Next, we want to write it in the Slope/Intercept
Form, which basically means we need to solve for y: |
|
*Dist. the -7/2 through ( )
*Inverse of sub. 2 is add. 2
*Slope/intercept form of the line |
The equation of the line that passes through (-7, 2) and is parallel
to 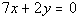is
y - 2 = -7/2(x + 7) OR y = -7/2x - 45/2. |
Answer/Discussion
to 2b
Passes through (3, -1) and is perpendicular to  . |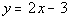
What are the two things we need to write an equation of a line????
If you said any point on the line and the slope, you are correct.
We have a point, however what about the slope? Does this mean
we can't work out the problem? You are not going to get off that
easily.
We need to do a little digging to get our slope.
As mentioned above, the slopes
of perpendicular lines are negative reciprocals of each other.
So, if we know the slope of the line perpendicular to our line, we have
it made.
Let's find the slope of the given line: |
|
*Slope/intercept form of the line |
Now keep in mind that this is not the equation of our line but of the
line parallel to our line. We needed to write it this way so we could
get the slope. And it looks like the slope is 2. Since our
line is perpendicular to a line that has a slope of 2, our line has
a slope of -1/2 (the negative reciprocal of 2).
OK, now we have our slope, which is -1/2. Now it is just like
problems in Tutorial 26: Equations
of Lines, we put the slope and one point into the point/slope equation.
Point/Slope Form: |
|
*Point/slope form of the line
|
Make sure that you are careful when one of your values is negative
and you have to subtract it as we did in line 2. y - (-1) is not the same as y - 1. |
Next, we want to write it in the Slope/Intercept
Form, which basically means we need to solve for y: |
|
*Dist. the -1/2 through ( )
*Inverse of add. 1 is sub. 1
*Slope/intercept form of the line
|
The equation of the line that passes through (3, -1) and is perpendicular
to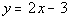
is y + 1 = -1/2(x - 3) OR y = -1/2x + 1/2. |
Last revised on Feb. 20, 2010 by Kim Seward.
All contents copyright (C) 2002 - 2010, WTAMU and Kim Seward. All rights reserved.
|
|
