Intermediate Algebra
Tutorial 4: Operations on Numbers
|
WTAMU > Virtual Math Lab > Intermediate Algebra
 Learning Objectives
After completing this tutorial, you should be able to:
- Add and subtract real numbers.
- Multiply and divide real numbers.
- Evaluate a numeric exponential expression.
- Evaluate a numeric radical expression.
- Use the order of operations appropriately.
|
Introduction
This tutorial reviews the adding, subtracting,
multiplying, and dividing
of real numbers as well as using exponents and roots. Once we have that
all down, we will put it all together using the order of
operations.
I have the utmost confidence that you are familiar with these
operations,
but sometimes the rules for negative numbers (yuck!) get a little mixed
up from time to time. So, it is good to go over them to make sure
you have them down. This is a very good topic to have down,
because
real numbers are EVERYWHERE.
Even in this day and age of calculators, it is very
important to know
these basic rules of operations on real numbers. Even if you are
using a calculator, you are the one that is putting the information
into
it, so you need to know things like when you are subtracting versus
multiplying
and the order that you need to put it in. Also, if you are using
a calculator you should have a rough idea as to what the answer should
be. You never know, you may hit a wrong key and get a wrong answer (it
happens to the best of us). Also, your batteries in your
calculator
may run out and you may have to do a problem by hand
(scary!!!).
You want to be prepared for those Murphy's Law moments.
We will start with the individual operations and then
mix ‘em up using
order of operations.
|
Tutorial
Adding Real Numbers
with the Same Sign
|
Step 1: Add the
absolute values.
Step 2: Attach
their common sign
to sum .
 Example
1: Find the sum -6 + (-8).
|
-6 + (-8) = -14
The sum of the absolute values would be 14 and their
common sign is
-. That is how we get the answer of -14.
You can also think of this as
money - I know
we can all relate to that. Think of the negative as a
loss. In this example, you can think of it as having lost 6
dollars
and then having lost another 8 dollars for a total loss of 14 dollars. |
Example
2: Find the sum -5.5 + (-8.7). |
-5.5 + (-8.7) = -14.2
The sum of the absolute values would be 14.2 and their
common sign is
-. That is how we get the answer of -14.2.
You can also think of this as
money - I know
we can all relate to that. Think of the negative as a
loss. In this example, you can think of it as having lost 5.5
dollars
and then having lost another 8.7 dollars for a total loss of 14.2
dollars. |
Adding Real Numbers
with Opposite Signs
|
Step 1: Take the
difference of the absolute
values.
Step 2: Attach the
sign of the number
that has the higher absolute value. |
Example
3: Find the sum -8 + 6. |
-8 + 6 = -2.
The difference between 8 and 6 is 2 and the sign of 8
(the larger absolute
value) is -. That is how we get the answer of -2.
Thinking in terms of money: we
lost
8 dollars and got back 6 dollars, so we are still in the hole 2 dollars. |
Example
4: Find the sum  . |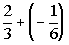
|
*Mult. top and bottom of first
fraction
by 2 to get the LCD of 6
*Take the difference of the
numerators
and write over common denominator 6
*Reduce fraction
|
The difference between 4/6 and 1/6 is 3/6 = 1/2 and the
sign of 4/6
(the larger absolute value) is +. That is how we get the
answer
of 1/2.
Thinking in terms of money: we
had
2/3 of a dollar and lost 1/6 of a dollar, so we would come out ahead
1/2
of a dollar.
Note that if you need help on fractions, click on this
link: Fractions |
Subtracting Real Numbers
a - b = a + (-b)
or
a - (-b) = a + b
|
In other words, to subtract b,
you add
the opposite of b.
Now, you do not have to write it out like this if you
are already comfortable
with it. This just gives you the thought behind it. |
Example
5: Find the difference -3 - 5. |
-3 - 5 = -3 + (-5) = -8.
Subtracting 5 is the same as adding a -5.
Once it is written as addition, I just follow
the rules for addition, as shown above, to complete for an
answer
of -8. |
Example
6: Find the difference -3 - (-5). |
-3 - (-5) = -3 + 5 = 2.
Subtracting -5 is the same as adding 5.
Once it is written as addition, I just follow
the rules for addition, as shown above, to complete for an
answer
of 2. |
|
Multiplying or Dividing Real
Numbers
|
Since dividing is the same as multiplying by the
reciprocal, dividing
and multiplying have the same sign rules.
Step 1: Multiply or
divide their absolute
values.
Step 2: Put the correct
sign.
If the two numbers have the same sign,
the product or quotient
is positive.
If they have opposite signs, the product
or quotient is negative. |
|
Example
7: Find the product (-4)(3). |
(-4)(3) = -12.
The product of the absolute values 4 x 3 is 12 and they
have opposite
signs, so our answer is -12. |
Example
8: Find the product  . |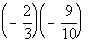
|
*Mult. num. together
*Mult. den. together
*(-)(-) = (+)
*Reduce fraction |
The product of the absolute values -2/3 x -9/10 is
18/30 = 3/5 and
they have the same sign, so that is how we get the answer 3/5.
Note that if you need help on fractions, click on this
link: Fractions |
Example
9: Find the quotient (-10)/(-2). |
(-10)/(-2) = 5
The quotient of the absolute values 10/2 is 5 and they
have the same
signs, so our answer is 5. |
Example
10: Find the quotient  . |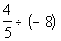
|
*Div. is the same as mult. by
reciprocal
*Mult. num. together
*Mult. den. together
*(+)(-) = -
*Reduce fraction |
The quotient of the absolute values 4/5 and 8 is 4/40 =
1/10 and they
have opposite signs, so our answer is -1/10.
Note that if you need help on fractions, click on this
link: Fractions |
Multiplying by and
Dividing into Zero
a(0) = 0
and
0/a = 0 (when a does not equal 0)
|
In other words, zero (0) times any real number is zero
(0) and zero
(0) divided by any real number other than zero (0) is zero (0). |
Example
11: Find the product 0(½). |
0(½) = 0
Multiplying any expression by 0 results in an answer
of 0. |
Example
12: Find the quotient 0/5. |
0/5 = 0
Dividing 0 by any expression other than 0 results in
an answer of
0. |
|
Dividing by Zero
a/0 is undefined
|
Zero (0) does not go into any number, so whenever you
are dividing
by zero (0) your answer is undefined.
Example
13: Find the quotient 5/0. |
5/0 = undefined.
Dividing by 0 results in an undefined answer. |
Definition of Exponents
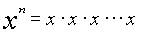
(note there are n x's in the product)
x = base, n =
exponent
|
Exponents are another way to
write multiplication.
The exponent tells you how many
times a base
appears in a PRODUCT.
Example
14: Evaluate  .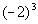
|
|
*Write the base -2 in a
product 3 times
*Multiply |
Example
15: Evaluate  . |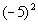
|
*Write the base -5 in a product 2
times
*Multiply
|
Note how I included the - when I expanded this
problem out.
If the - is inside the ( ) of an exponent, then it is included as part
of the base. |
Example
16: Evaluate  . |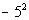
|
*Negate 5 squared
*Put a - in front of 5 written in
a product
2 times
*Multiply |
Hey, this looks a lot like example 15!!!! It
may look alike,
but they ARE NOT exactly the same. Can you see the difference
between
the two?? Hopefully, you noticed that in example 15, there was a
( ) around the - and the 5. In this problem, there is no (
).
This means the - is NOT part of the base, so it will not get expanded
like
it did in example 15. It is interpreted as finding the negative
or
opposite of 5 squared. |
|
Principal nth Root
|
Things to note about radicals
in general,
- When there is no index number n,
it is
understood
to be a 2 or square root.
- When looking for the nth radical or nth root, you
want the expression
that
when you raise it to the nth power you would get the radicand (what is
inside the radical sign).
|
Example
17: Find the root:  . |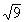
The thought behind this is that we are looking for the
square root
of 9. This means we are looking for a number that when we
square
it we get 9. Since 3 squared is 9, 3 is the square root
of 9.
Note that we are only interested in the principal root
and since 9 is
positive and there is not a sign in front of the radical, our answer is
positive 3. If there had been a negative in front of the radical
our answer would have been -3. |
Example
18: Find the root:  . |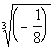
Contrary to popular belief, not
every radical
is a square root. If there is an index or root number written,
make
sure you take the appropriate root.
Now we are looking for the third
or cube root
of -1/8, which means we are looking for a number that when we cube it
we
get -1/8.
Since -1/2 cubed is -1/8, our
answer is going
to be -1/2. |
.
|
Order of Operations
Please Parenthesis
or grouping symbols
Excuse Exponents
(and radicals)
My Dear Multiplication/Division
left to right
Aunt Sally Addition/Subtraction
left to right |
As you know, life (as well as algebra) is not always as
cut and dry
like the above examples. It is very important for you to
understand
each individual operation first (that is what we were doing in the
above
examples) and now we will put them together and mix them all about.
When you do have more than one mathematical operation,
you need to use
the order of operations as listed above. You may have already heard of
the saying "Please Excuse My Dear Aunt Sally". It is just a way
to
help you remember the order you need to go in when applying the order
of
operations.
Example
19: Simplify  . |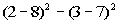
|
*Work inside ( )
*Exponents
*Subtraction
|
Example
20: Simplify  . |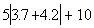
An absolute value is like a
fancy grouping
symbol. So, if you have one, you need to do what is inside first,
before tackling the other operations that are on the outside of it, as
shown below.
Using the Order of Operations we get: |
|
*Work inside | |
*Multiply
*Add
|
Example
21: Find the value of the expression when x = -1 and y = 5.
|
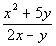
When you have a fraction, like
the one in
this example, there are hidden grouping symbols. The
fraction
bar separates the numerator from the denominator. You need to
think
of it as if there is a ( ) around the numerator and one
around
the denominator. In other words, when you have a problem like
this
one, you need to find the numerator and denominator first, before you
deal
with the fraction bar (division).
Plugging in values
for the variables
and evaluating the expression using the Order of
Operations we get: |
|
*Replace x with -1 and y with 5
*Exponent in num.
*Multiply in num. and den.
*Add in num. and subtract in
den.
|
Practice Problems
These are practice problems to help bring you to the
next level.
It will allow you to check and see if you have an understanding of
these
types of problems. Math works just like
anything
else, if you want to get good at it, then you need to practice
it.
Even the best athletes and musicians had help along the way and lots of
practice, practice, practice, to get good at their sport or instrument.
In fact there is no such thing as too much practice.
To get the most out of these, you should work the
problem out on
your own and then check your answer by clicking on the link for the
answer/discussion
for that problem. At the link you will find the answer
as well as any steps that went into finding that answer. |
 Practice
Problems 1a - 1c: Find the sum or difference.
Practice
Problems 2a - 2b: Find the product or quotient.
Practice
Problems 3a - 3c: Evaluate.
Practice
Problems 4a - 4b: Find the root.
Practice
Problems 5a - 5b: Simplify the expression.
Practice
Problem 6a: Find the value of the expression
when a = 3 and b = -2.
Need Extra Help on these Topics?
Last revised on June 10, 2011 by Kim Seward.
All contents copyright (C) 2002 - 2011, WTAMU and Kim Seward. All rights reserved.
|
