Intermediate Algebra
Tutorial 2: Algebraic Expressions
|
WTAMU > Virtual Math Lab > Intermediate Algebra
 Learning Objectives Learning Objectives
After completing this tutorial, you should be able to:
- Know what a variable is.
- Know what an algebraic expression is.
- Evaluate an algebraic expression given a value for a variable.
- Translate an English phrase into an algebraic expression
|
 Introduction Introduction
This tutorial will go over some key definitions and phrases used when
specifically working with algebraic expressions as well as evaluating them.
It is very IMPORTANT that you understand some of the math lingo that is
used in an algebra class, otherwise it may all seem Greek to you. Knowing
the terms and concepts on this page will definitely help you build an understanding
of what a variable is and get you more comfortable working with them. Variables are a HUGE part of algebra, so it is very important for you to
feel at ease around them in order to be successful in algebra. So
let's get going and help you get on the road to being variable savvy. |
 Tutorial Tutorial
A variable is a letter that represents a number.
Don't let the fact that it is a letter throw you. Since it represents
a number, you treat it just like you do a number when you do various mathematical
operations involving variables.
x is a very common variable that is used
in algebra, but you can use any letter (a, b, c, d,
....) to be a variable. |
An algebraic expression is a number, variable or combination
of the two connected by some mathematical operation like addition, subtraction,
multiplication, division, exponents, and/or roots.
2x + y, a/5,
and 10 - r are all examples of algebraic expressions. |
You evaluate an expression by replacing the variable with the
given number and performing the indicated operation. |
When you are asked to find the value of an expression, that
means you are looking for the result that you get when you evaluate the
expression. |
So keep in mind that vary means to change - a variable allows an
expression to take on different values, depending on the situation.
For example, the area of a rectangle is length times width. Well,
not every rectangle is going to have the same length and width, so we can
use an algebraic expression with variables to represent the area and then
plug in the appropriate numbers to evaluate it. So if we let the
length be the variable l and width be w,
we can use the expression lw. If a given
rectangle has a length of 4 and width of 3, we would evaluate the expression
by replacing l with 4 and w with 3 and multiplying to get a value of 4 times 3 or 12.
Let's step through some examples that help illustrate these ideas.
 Example
1: Find the value of the algebraic expression at the given
value. Example
1: Find the value of the algebraic expression at the given
value.
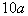 when a = 15. when a = 15.
|
Remember that when a number is directly in front of a variable (there
is no + or - between them), like in this example, that means that when
you evaluate this expression you will be multiplying 10 times whatever
value a is.
Replace a with 15 and then multiply: |
|
*Replace a with 15
*( ) is another way to write mult.
*Multiply together |
That wasn't so bad, let's look at another example. |
 Example
2: Example
2: Find the value of the algebraic expression at
the given value.
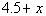 when x = 3.2 when x = 3.2
|
Replace x with 3.2 and then add: |
|
*Replace x with 3.2
*Add the numbers
|
Sometimes, there are more than one variable involved, you just extend
this basic idea to how ever many variable you have. For each variable,
you simply replace it with it's corresponding value, as this next example
illustrates.
 Example
3: Find the value of the algebraic expression at the given
value. Example
3: Find the value of the algebraic expression at the given
value.
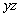 when when 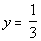 and
and 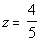
|
Keep in mind that when you see two variables written side by side,
like y and z are
in this example, that means that y and z are
being multiplied together.
Replace y with 1/3 and z with 4/5 and multiply: |
|
*Replace y with
1/3 and z with 4/5
*Multiply the fractions together
|
Note that if you need to review multiplying fractions go to this link: fractions |
 Example
4: Example
4: If it costs $15 per cd at a local Entertainment
store, then we can use the algebraic expression 15x, where x represents
the number of cd's purchased, to find the cost of buying x cd's.
How much would it cost to buy 7? |
Even though the information was given in a little bit different form
than the first three examples, it still uses the same basic concept - replace
the variable with the given value and then evaluate the expression. |
|
*Replace x with 7
*Multiply together
|
Translating an
English Phrase Into an
Algebraic Expression
|
Sometimes, you find yourself having to write out your own algebraic
expression based on the wording of a problem.
In that situation, you want to
- read the problem carefully,
- pick out key words and phrases and determine their equivalent mathematical
meaning,
- replace any unknowns with a variable, and
- put it all together in an algebraic expression.
The following are some key words and phrases and
their translations: |
Addition: sum, plus, add to, more than,
increased by, total |
Subtraction: difference of, minus,
subtracted from, less than, decreased by, less |
Multiplication: product, times, multiply,
twice, of |
Division: quotient divide, into,
ratio |
 Example
5: Example
5: Write the phrase as an algebraic expression.
The sum of a number and 10. |
In this example, we are not evaluating an expression, so we will not
be coming up with a value like we did in examples 1 - 4 above. However,
we are wanting to rewrite it as an algebraic expression.
It looks like the only reference to a mathematical operation is the
word sum - so what operation will we have in this expression?
If you said addition, you are correct!!!
The phrase 'a number' indicates that it is an unknown number - there
was no specific value given to it. So we will replace the phrase
'a number' with the variable x. We want
to let our variable represent any number that is unknown
Putting everything together, we can translate the given english phrase
with the following algebraic expression: |
The sum of a number and 10
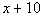
|
*'sum' = +
*'a number' = variable x
|
Let's try another!
 Example
6: Write the phrase as an algebraic expression. Example
6: Write the phrase as an algebraic expression.
The product of 5 and a number. |
Again, we are wanting to rewrite this as an algebraic expression, not
evaluate it.
This time, the phrase that correlates with our operation is 'product' - so what operation will we be doing this time? If you said multiplication,
you are right on.
Again, we have the phrase 'a number', which again is going to be replaced
with a variable, since we do not know what the number is.
Let's see what we get for this answer: |
The product of 5 and a number
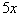
|
*'product' = multiplication
*'a number' = variable x
|
 Example
7: Example
7: Write the phrase as an algebraic expression. 3 less than twice a number |
First of all, we have the phrase 'less than' which mathematically
translates as subtraction. You need to be careful with this phrase,
it is very tempting to start off with 3 and put your subtraction sign after
the 3. However, think about it, if you want 3 less than something,
you are 3 below it. In order to be 3 below something, you would have to
subtract the 3!!! So you would not have 3 minus, but minus 3 as PART
of your expression.
The other part of the expression involves the phrase 'twice a number'.
'Twice' translates as two times a number and, as above, we will replace
the phrase 'a number' with our variable x.
Putting this together we get: |
3 less than twice a number
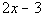
|
*'less than' = -
*'twice' = 2 times
*'a number' = variable x |
 Example
8: Example
8: Write the phrase as an algebraic expression. The quotient of 3 and the difference of a number and 2. |
First of all, the term 'quotient' is going to be replaced with
what mathematical operation? If you said division, you are
right on the mark!!
Note how 3 immediately follows the phrase 'the quotient of', this means
that 3 is going to be in the numerator. The phrase that immediately
follows the word 'quotient' is going to be in the numerator of it.
After the word 'and', you have the phrase 'the difference of a number
and 2'. That is the second part of your quotient which means it will
go in the denominator. And what operation will we have when we do
write that difference down below? I hope you said subtraction.
Let's see what we get when we put all of this together: |
The quotient of 3 and the difference of a number and 2.
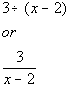
|
*'quotient' = division
*'difference' = -
*'a number' = variable x
|
Now it is your turn, the next section are problems that you can
practice on to see if you are understanding these topics. |
 Practice Problems Practice Problems
These are practice problems to help bring you to the
next level.
It will allow you to check and see if you have an understanding of
these
types of problems. Math works just like
anything
else, if you want to get good at it, then you need to practice
it.
Even the best athletes and musicians had help along the way and lots of
practice, practice, practice, to get good at their sport or instrument.
In fact there is no such thing as too much practice.
To get the most out of these, you should work the
problem out on
your own and then check your answer by clicking on the link for the
answer/discussion
for that problem. At the link you will find the answer
as well as any steps that went into finding that answer. |
 Practice
Problems 1a - 1c: Find the value of the algebraic expression at the given
replacement values. Practice
Problems 1a - 1c: Find the value of the algebraic expression at the given
replacement values.
1c. You need to know how much area of carpet to purchase to carpet
your rectangular floor. You will need to use the algebraic expression lw to find it's area, where l represents
the length of the rectangular floor and w is
the width of it. If your rectangular floor is 15 feet long and 8
feet wide, find how much area of carpet you would need to cover it.
(answer/discussion
to 1c) |
 Practice
Problems 2a - 2c: Write each phrase as an algebraic expression. Practice
Problems 2a - 2c: Write each phrase as an algebraic expression.
 Need Extra Help on these Topics? Need Extra Help on these Topics?

Last revised on June 10, 2011 by Kim Seward.
All contents copyright (C) 2002 - 2011, WTAMU and Kim Seward. All rights reserved.
|


