Answer/Discussion on Simplifying Radical Expressions

(Back to the tutorial on simplifying radical expressions)

Intermediate Algebra
Answer/Discussion to Practice Problems
on Simplifying Radical Expressions

Answer/Discussion to 1a

*Use the prod. rule of radicals to rewrite

Note that both radicals have an index number of 5, so we were able to put their product together under one radical keeping the 5 as its index number.

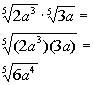
Since we cannot take the fifth root of and does not have any factors we can take the fifth root of, this is as simplified as it gets.

(return to problem 1a)

Answer/Discussion to 2a

*Use the quotient rule of radicals to rewrite

*Square root of 49 is 7

Since we cannot take the square root of 5 and 5 does not have any factors that we can take the square root of, this is as simplified as it gets.

(return to problem 2a)

Answer/Discussion to 3a

Even though 40 is not a perfect cube, it does have a factor that we can take the cube root of.

Check it out:

*Rewrite 40 as (8)(5)

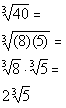
*Use the prod. rule of radicals to rewrite
*The cube root of 8 is 2

In this example, we are using the product rule of radicals in reverse to help us simplify the cube root of 40. When you simplify a radical, you want to take out as much as possible. The factor of 40 that we can take the cube root of is 8. We can write 40 as (8)(5) and then use the product rule of radicals to separate the 2 numbers. We can take the cube root of 8, which is 2, but we will have to leave the 5 under the cube root.

(return to problem 3a)

Answer/Discussion to 3b

Even though

is not a perfect square, it does have a factor that we can take the square root of.

Check it out:

*Rewrite as

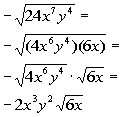
*Use the prod. rule of radicals to rewrite
*The square root of is

In this example, we are using the product rule of radicals in reverse to help us simplify the square root of

. When you simplify a radical, you want to take out as much as possible.

The factor of that we can take the square root of is . We can write as and then use the product rule of radicals to separate the two numbers. We can take the square root of which is , but we will have to leave the rest of it under the square root.

(return to problem 3b)

Answer/Discussion to 4a

*Use the quotient rule of radicals to rewrite

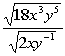
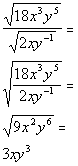
*Simplify fraction
*Take the square root

Note that both radicals have an index number of 2, so we are able to put their quotient together under one radical keeping the 2 as its index number. Since the radicand is a perfect square, we are able to take the square root of the whole thing, which leaves us with nothing under the radical sign.

(return to problem 4a)

(Back to the tutorial on simplifying radical expressions)