

![]()
AND
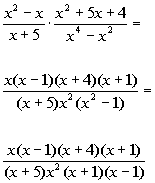
In the denominator we factored a GCF and a difference of squares.
AND
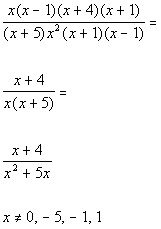
*Multiply the den. out
*Excluded values of the original den.
![]()
AND
Step 2: Multiply
the rational expressions as shown above.
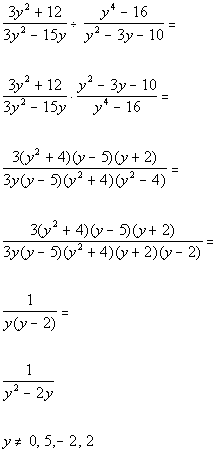
*Rewrite as mult. of reciprocal
*Factor the num. and den.
*Simplify by div. out the common factors of
3, (y^2 + 4),
(y - 5), and (y + 2)
*Multiply the den. out
*Excluded values of the original den. of product
In the denominator we factored a GCF
and a difference of squares.
Note that the values that would be excluded from the domain are 0,
5, -2, and 2. Those are the values that makes the original
denominator of the product equal to 0.
Last revised on Dec. 15, 2009 by Kim Seward.
All contents copyright (C) 2002 - 2010, WTAMU and Kim Seward. All rights reserved.