College Algebra
Tutorial 8: Simplifying Rational Expressions
 Learning Objectives Learning Objectives
After completing this tutorial, you should be able to:
- Find the domain of a rational expression.
- Simplify a rational expression.
|
 Introduction Introduction
Do you ever feel like running and hiding when you
see a fraction? If so, you are not alone. But don't fear!
Help is here!
Hey, that rhymes. Anyway, over the next several tutorials we will
be showing you several aspects of rational expressions
(fractions).
In this section we will be simplifying them. Again, we will be
putting
your knowledge of factoring to the test. Factoring plays a big
part
of simplifying these rational expressions. So if you feel the
need
to review factoring go back to
Tutorial
7: Factoring Polynomials. I think you are ready to tackle
these rational expressions. |
 Tutorial Tutorial
|
Rational
Expression
A rational
expression is one
that
can be written in
the form
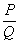
where P and Q are polynomials
and Q does not equal 0.
|
An example of a rational expression is:
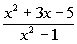
|
|
Domain of
a Rational Expression
|
With rational functions, we
need to watch
out for values that cause our denominator to be 0. If
our denominator is 0, then we have an undefined value.
So, when looking for the domain of a given rational
function, we use
a back door approach. We find the values that we cannot use,
which
would be values that make the denominator 0. |
Our restriction is that the denominator of a fraction
can never be
equal to 0.
So to find what values we need to exclude, think of what
value(s) of x,
if any, would cause the denominator to be 0. |
This give us a better look at it.
Since 1 would make the first factor in the denominator
0, then 1
would have to be excluded.
Since - 4 would make the second factor in the
denominator 0, then -
4 would also have to be excluded. |
Fundamental
Principle of
Rational
Expressions
For any
rational expression 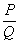 ,
and any polynomial R, where , ,
and any polynomial R, where ,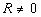 ,
then ,
then
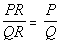
|
In other words, if you multiply the EXACT SAME thing
to the numerator
and denominator, then you have an equivalent rational expression.
This will come in handy when we simplify rational
expressions, which
is coming up next. |
Simplifying
(or reducing)
a
Rational Expression
|
Step 1: Factor the numerator
and the denominator. |
Step 2: Divide out all
common factors that the numerator and the denominator have. |
 Example
2: Simplify and find all numbers that must be
excluded
from the domain of the simplified rational expression: Example
2: Simplify and find all numbers that must be
excluded
from the domain of the simplified rational expression: 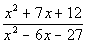 . .
 View a video of this example View a video of this example
|
Step 1: Factor the numerator
and the denominator
AND |
Step 2: Divide out all
common factors that the numerator and the denominator have. |
|
*Divide out the common factor
of (x + 3)
*Rational expression simplified
|
To find the value(s) needed to be excluded from the
domain, we need
to ask ourselves, what value(s) of x would
cause our denominator to be 0?
Looking at the denominator x - 9, I would
say it would have to be x = 9.
Don’t
you agree?
9 would be our excluded value.
|
 Example
3: Simplify and find all numbers that must be
excluded
from the domain of the simplified rational expression: Example
3: Simplify and find all numbers that must be
excluded
from the domain of the simplified rational expression: 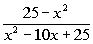 . .
 View a video of this example View a video of this example
|
Step 1: Factor the numerator
and the denominator
AND |
Step 2: Divide out all
common factors that the numerator and the denominator have. |
|
*Factor out a -1 from (5 - x)
*Divide out the common factor
of (x - 5)
*Rational expression simplified |
Note that 5 - x and x - 5 only differ by signs, in other
words
they are opposites of each other. In that case, you can factor a
-1 out of one of those factors and rewrite it with opposite signs, as
shown
in line 3 above.
To find the value(s) needed to be excluded from the
domain, we need
to ask ourselves, what value(s) of x would
cause our denominator to be 0?
Looking at the denominator x - 5, I would
say it would have to be x = 5.
Don’t
you agree?
5 would be our excluded value. |
 Practice Problems Practice Problems
These are practice problems to help bring you to the
next level.
It will allow you to check and see if you have an understanding of
these
types of problems. Math works just like
anything
else, if you want to get good at it, then you need to practice
it.
Even the best athletes and musicians had help along the way and lots of
practice, practice, practice, to get good at their sport or instrument.
In fact there is no such thing as too much practice. To get the most out of these, you should work the
problem out on
your own and then check your answer by clicking on the link for the
answer/discussion
for that problem. At the link you will find the answer
as well as any steps that went into finding that answer. |
 Practice
Problem 1a: Find all numbers that must be
excluded from the domain
of the given rational expression. Practice
Problem 1a: Find all numbers that must be
excluded from the domain
of the given rational expression.
 Practice
Problems 2a - 2b: Simplify and find all numbers that
must be excluded
from the domain of the simplified rational expression. Practice
Problems 2a - 2b: Simplify and find all numbers that
must be excluded
from the domain of the simplified rational expression.
 Need Extra Help on these Topics? Need Extra Help on these Topics?

Videos at this site were created and produced by Kim Seward and Virginia Williams Trice.
Last revised on Dec. 14, 2009 by Kim Seward.
All contents copyright (C) 2002 - 2010, WTAMU and Kim Seward. All rights reserved.
|
|


